Introduzione
Salve lettori, questa pagina è stata creata per riassumere o ampliare gli appunti che prendiamo a lezione, questi appunti possono servire per capire meglio l’argomento e non possono essere capiti completamente se non si seguono le lezioni. Se trovate errori o parti poco chiare vi prego di segnalarlo così provederemo a corregere. Buona lettura -NP
Capitolo Uno: Il Diodo
Il diodo non è altro che un componente NON-lineare che fa passare la corrente in un verso e ne impedisce il movimento nel verso opposto.
Ha un comportamento NON-lineare, per essere precisi di tipo semi-esponenziale, avendo polarizzazione diretta, inversa e avendo un possibile evento di Breakdown.
1.1 Comportamento fisico-chimico
Per capire ciò bisogna prima fare un piccolo passo indietro, dobbiamo partire dall’atomo di Silicio, ora tanti atomi di silicio vicini a temperature superiori allo 0K fanno ciò che gli atomi fanno, dunque rottura dei legami e successiva riformazione di questi ultimi con altri atomi con posti liberi. Ora se sostituissi un atomo di silicio con uno di boro (1 elettrone in meno) farei una procedura chiamata DROGAGGIO di tipo ACCETTORE, visto che il boro ha uno spazio libero tende a chiedere un elettrone per andare in stabilità, se lo sostituissi con un atomo di fosforo (un elettrone in più) il drogaggio è di tipo DONORE, avendo un elettrone in più cede per andare in stabilità, quindi qui si spostano più elettroni.
Detto questo cosa succede ?
Dobbiamo immaginarci il diodo come un rettagolo pieno di atomi di silicio, dentro questo rettangolo ci sono cariche positive e cariche negative, queste cariche si bilanciano in due zone: catodo (-) e anodo (+).
Le cariche positive nello spostarsi dal catodo all’anodo perdono qualche carica positiva, idem gli elettroni, creando una zona non bilanciata, che crea un campo elettrico che impedisce ulteriori diffusioni.
1.2 Polarizzazione Inversa e Diretta
Detto ciò, in polarizzazione inversa questa zona aumenta e ciò impedisce alla corrente di passare. In polarizzazione diretta la zona si restringe e la corrente aumenta, la tensione rimane costante a 0,7 V.
1.3 Evento di Breakdown
In polarizzazione inversa può avvenire il Breakdown, sostanzialmente la tensione diventa costante a un valore V_{BD} e la corrente aumenta (diodo bruciato).
1.4 Formule
La corrente del diodo I_D è legata esponenzialmente alla tensione del diodo V_D.
I_D=I_{SO}(e^\frac{V_D}{V_{TH}}-1)
I_{SO}=qA^2n_i(\frac{D_p}{N_DL_P}+\frac{D_n}{N_AL_n})
Parametri:
(n_i,D_P,D_n) fisici.
(A) geometrici.
(N_A,N_D) drogaggio di giunzioni.
(L_P,L_n) profili.
A P.I. la corrente vale -I_{SO}.
1.5 Tipi di diodo
- Diodo Zener V_{PD}=5V, v_{PI}=-20V. Particolarità: non si può
bruciare.

- Diodo Schottky V_{PD}=0.2V, V_{BD}<50V.
- Diodo LED Emettono luce in P.D. V_{VD} varia a seconda del colore.
- Fotodiodo riceve luce e lo trasforma in segnale elettrico.

- Diodo Varicap possiede una capacità di giunzione C_j.
1.6 Potenza Dissipata
Vista la caratteristica dei diodi di avere 3 tipi di funzinamento diversi, calcolare la potenza dissipata dal diodo non è passeggiata.
In teoria la potenza dissipata in questi 3 periodi (T) è:
P_D=\frac{E_D}{T}=\frac{1}{T}*\int_{0}^{T} V_D(t)i_D(t)dt
Per facilitare tale impresa la dividiamo secondo i 3 periodi e poi facciamo la somma (un po’ come nella sovrapposizione degli effetti).
- In diretta, abbiamo V costante:
E_{D,F} = V_F \int_{t \in T_F} i_D(t) dt
- In inversa, i_D(t)=I_S (costante), lo si approssima a 0:
E_{D,R}=I_S \int_{t \in T_R} v_d(t)dt \to 0
- In Breakdown (se non mi polverizza il diodo) ha V_{BD} costante:
E_{D,BD}= V_{BD} \int_{t \in T_{BD}} i_D(t) dt
F=forward, R=reverse.
Quindi P_D= \frac{1}{T}(V_F \int_{t \in T_F} i_D(t)dt + I_S \int_{t \in T_R} v_D(t) dt + V_{BD} \int_{t \in T_{BD}} i_D(t)dt)
Con I_S \to 0
P_D=V_F(\frac{1}{T} \int_{t \in T_F} i_D(t)dt) + V_{BD}(\frac{1}{T} \int_{t \in T_{BD}} i_D(t)dt)
Capitolo Due: Circuiti con diodo
Allora cerchiamo di capire perchè il modello linerare è comodo per “cookare” (prof la amo) i circuiti con i diodi.
2.1 Metodo analitico
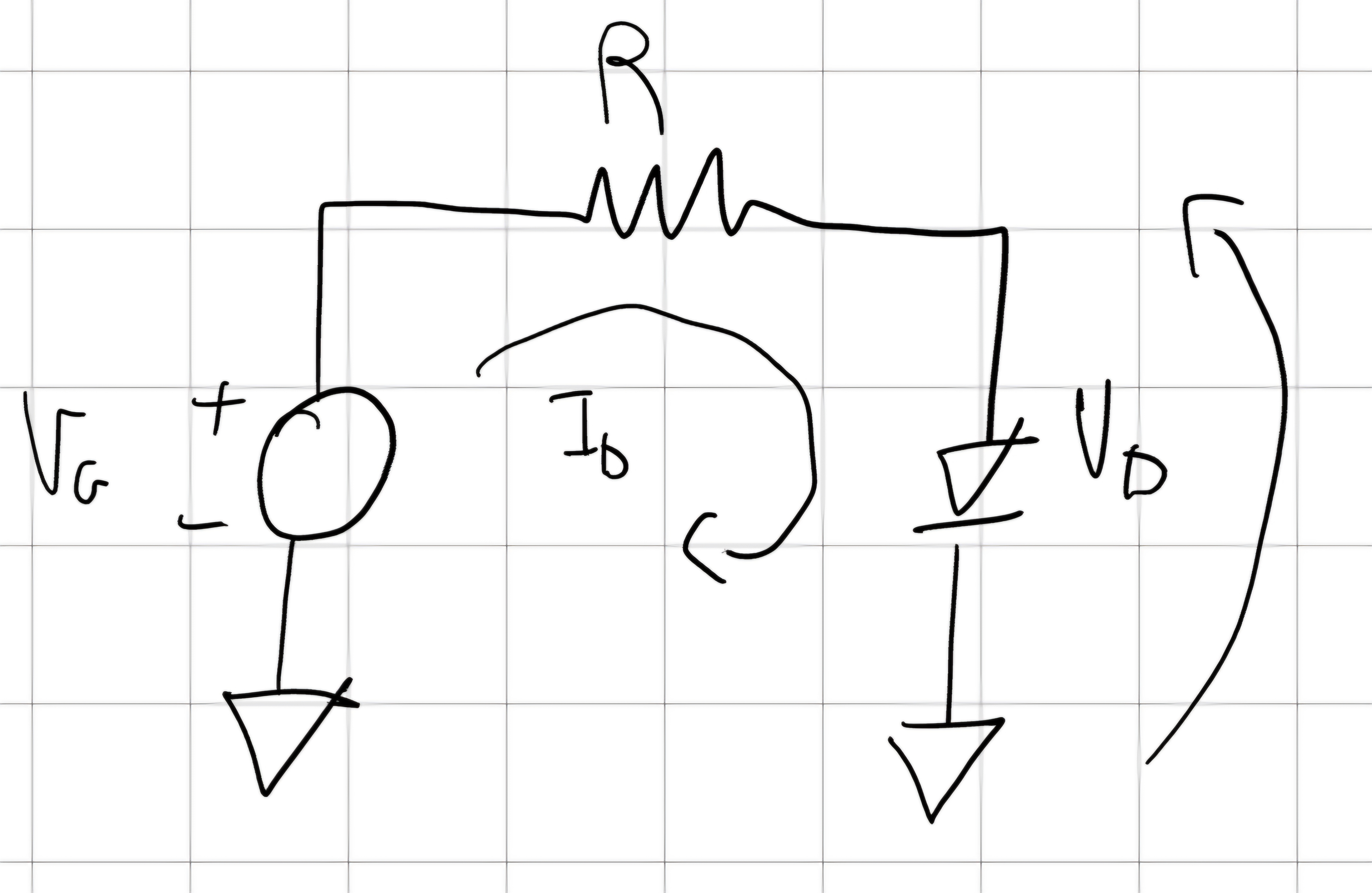
KCL, KVL \begin{cases} I_R=I_D\\ V_G=V_R+V_D \end{cases}
Legge di Ohm \begin{cases} V_R=RI_R\\ I_D=I_S(e^{\frac{V_D}{V_{TH}}}-1) \end{cases}
Semplificando \begin{cases} V_D=V_G-RI_D\\ I_D=I_S(e^{\frac{V_G-RI_D}{V_{TH}}}-1) \end{cases}
Conti brutti da gestire.
2.2 Metodo Grafico
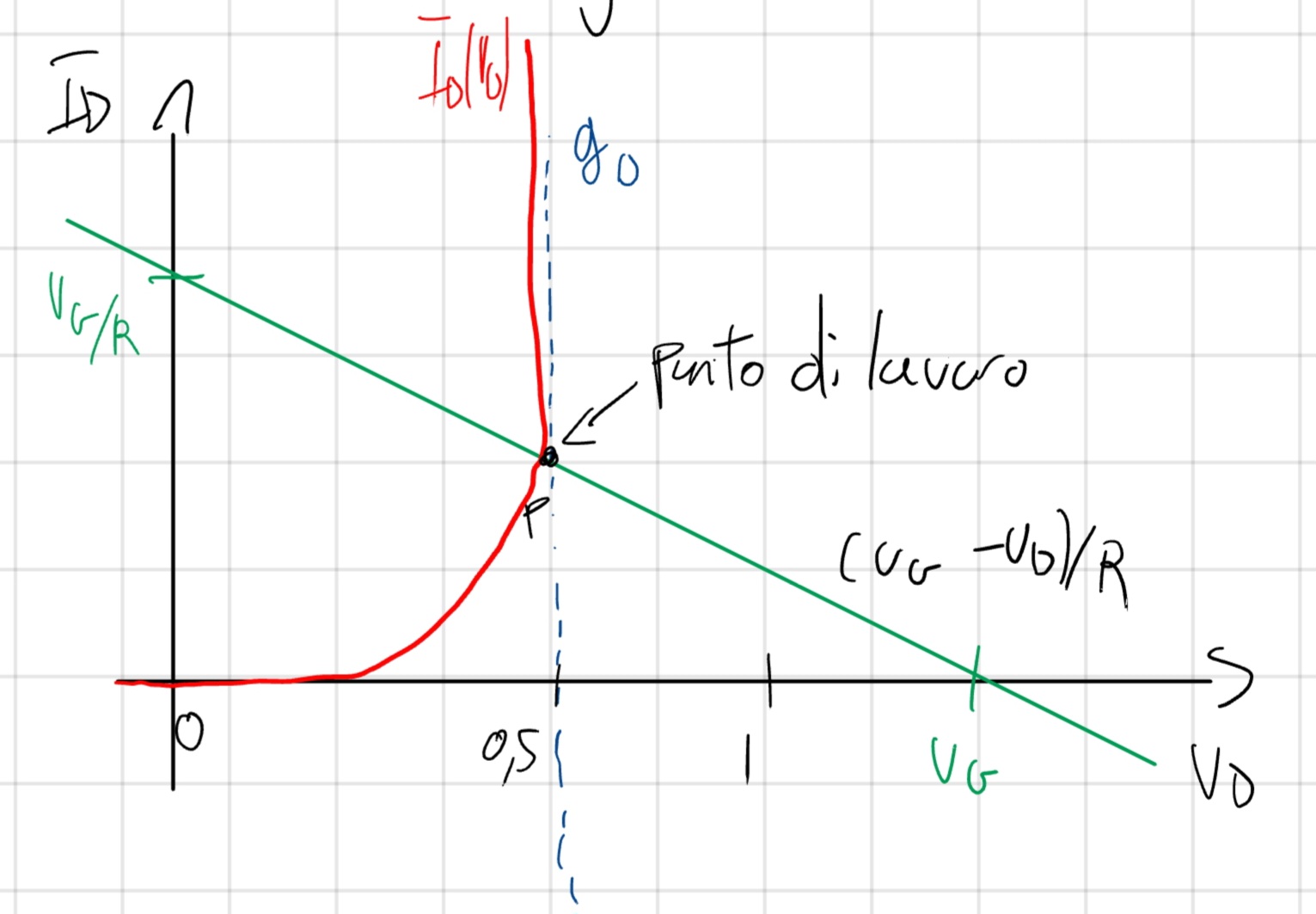
Molto bello ma molto poco pratico (guarda quanti bei colori (3)).
2.3 Modello Lineare (questo “cooka” bene)
Se I_D > 0\\ V_D=0,7 V\\ I_D= \frac{V_G-0,7V}{R}\\ \iff V_G>0,7V
Se V_D<0,7V\\ I_D=0A\\ V_D=V_G-0V \iff V_G=V_D
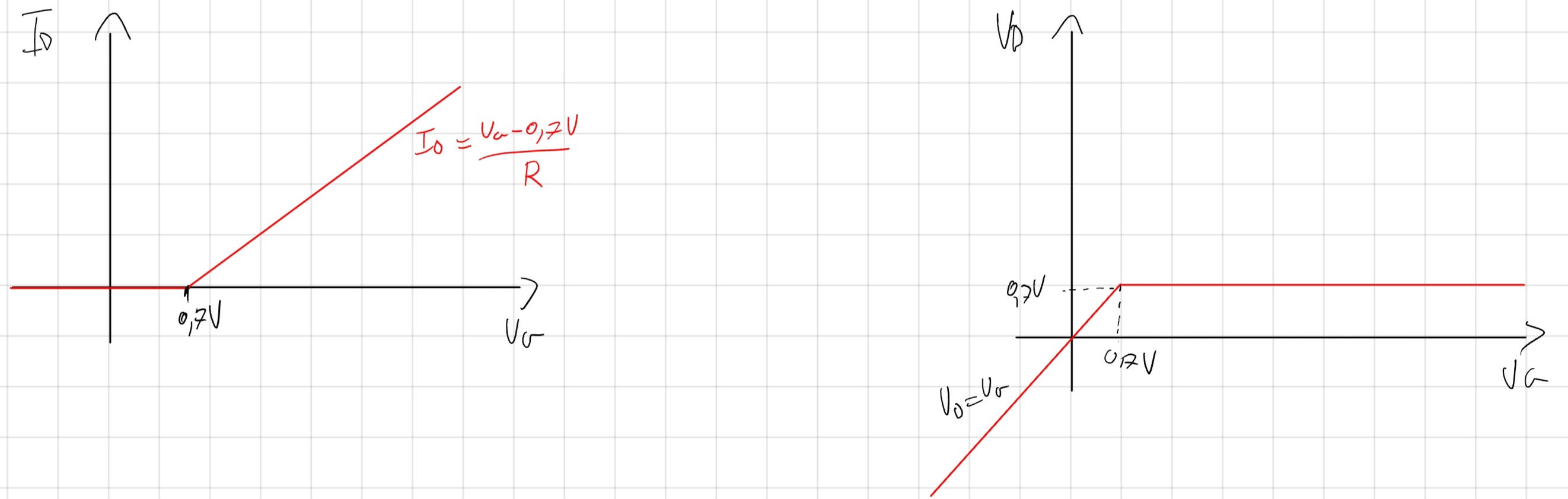
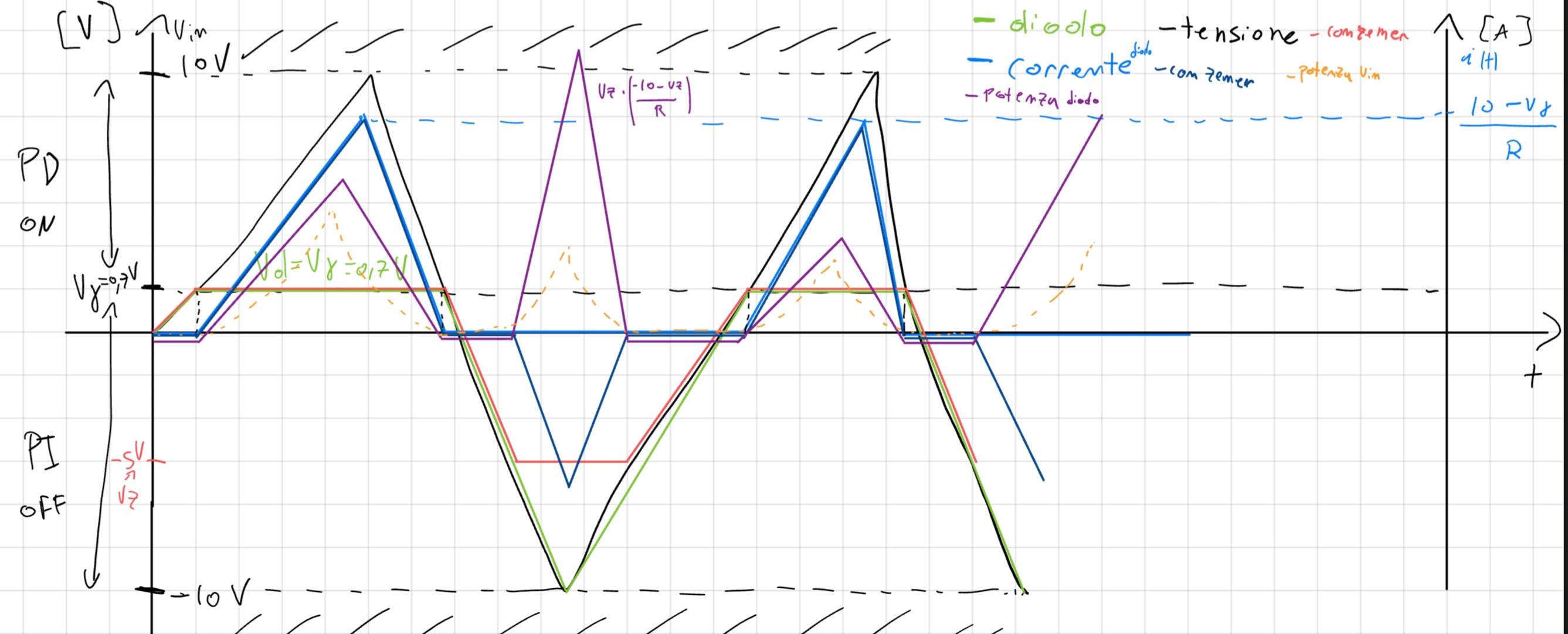
Capitolo Tre: MOSFET
3.1 Struttura
Dopo i diodi introduciamo un nuovo componente elettronico FONDAMENTALE, il MOSFET (che qualuno non riesce a pronunciare, ciao Andre ti voglio bene :) ).
Allora cerchiamo di capire cos’è e come funziona.
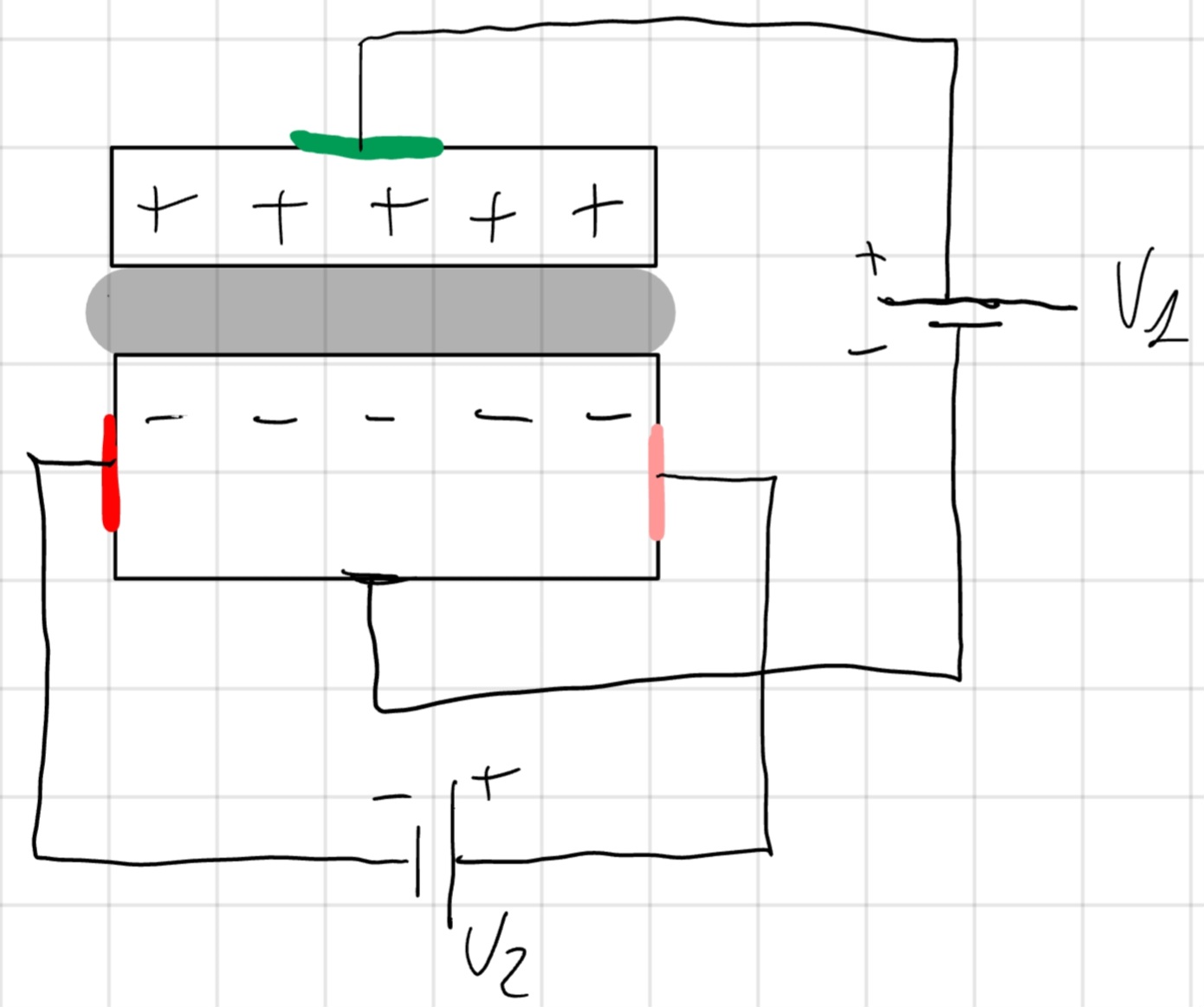
Allora questo è un MOSFET (bello vero?), partiamo dalla composizione: è un panino di metallo (parte superiore) metallo-ossido (parte inferiore) e silicio. L’ossido è il mio dielettrico (SiO_2).
È un condensatore-semiconduttore, il suo scopo è quello di creare carica libera.
È formato da tre terminali \textcolor{red}{source}, \textcolor{pink}{drain}, \textcolor{green}{gate}, e la corrente che scorre tra drain e gate dipende dalla tensione che viene applicata tra source e gate.
MOSFET sta per:
M.O.S. \to Metal Oxide Semiconductor, per la struttura.
F.E.T. \to Field Effect Transistor, per il funzionamento.
Ma come funziona ?
3.2 Funzionamento
Il funzionamento si basa sull’applicare una tensione agli elettrodi e indurre una carica Q=CV_1, applico poi una tensione V_2 al semiconduttore.
> carica indotta, > è la corrente.
A seconda della carica indotta ho 2 tipi di MOS:
- NMOS (elettroni)
- PMOS (lacune)
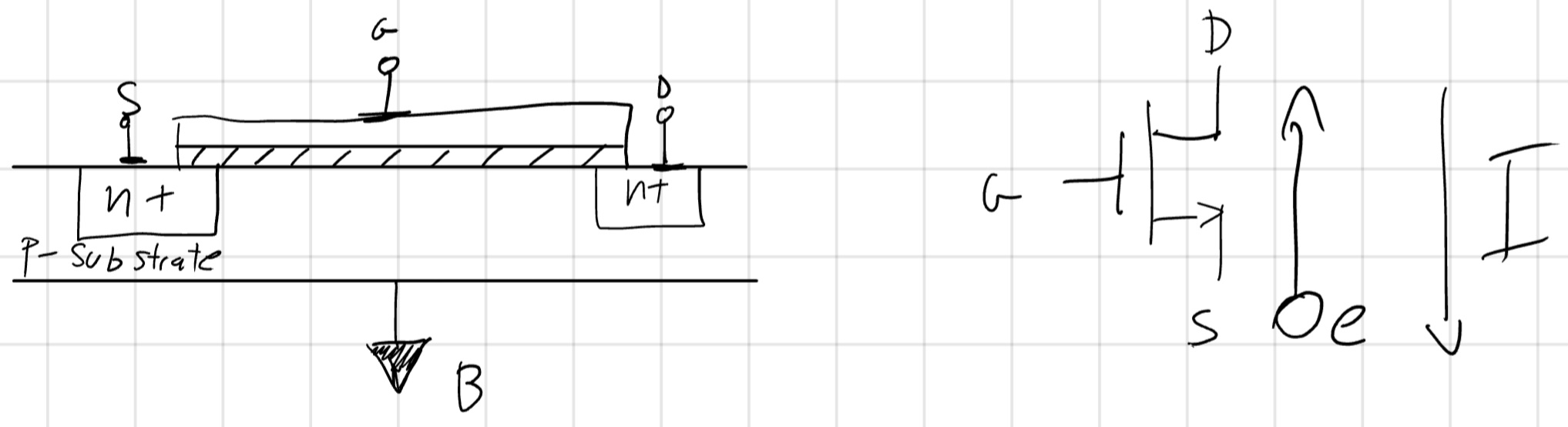
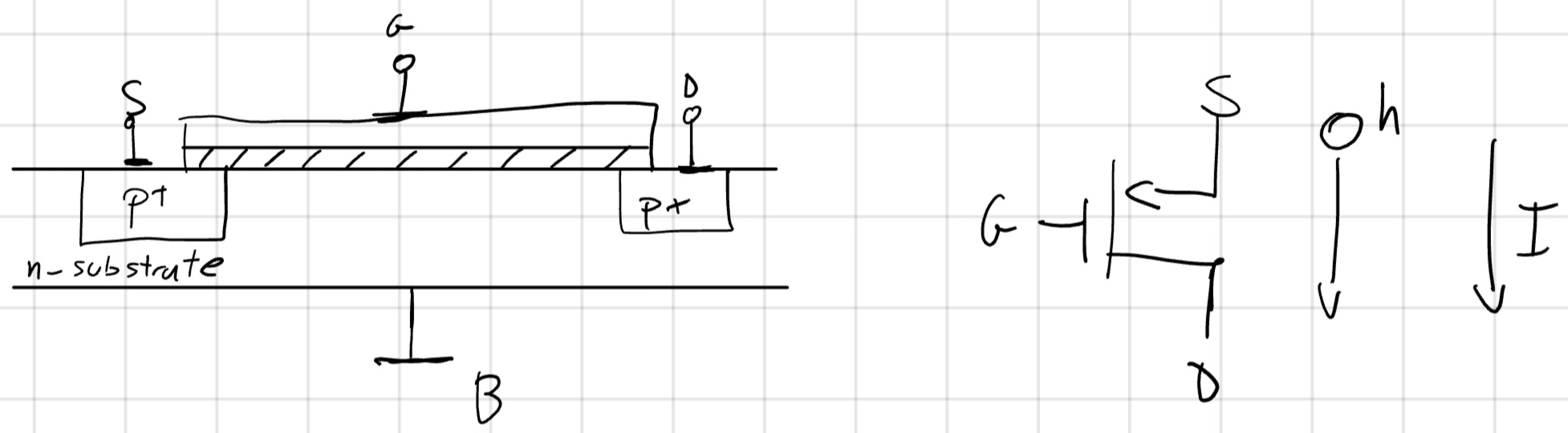
Per i ragazzi che come me si trovano disorientati quando vi è un cambio di rappresentazione ecco una breve spiegazione sul NMOS (idem al PMOS).
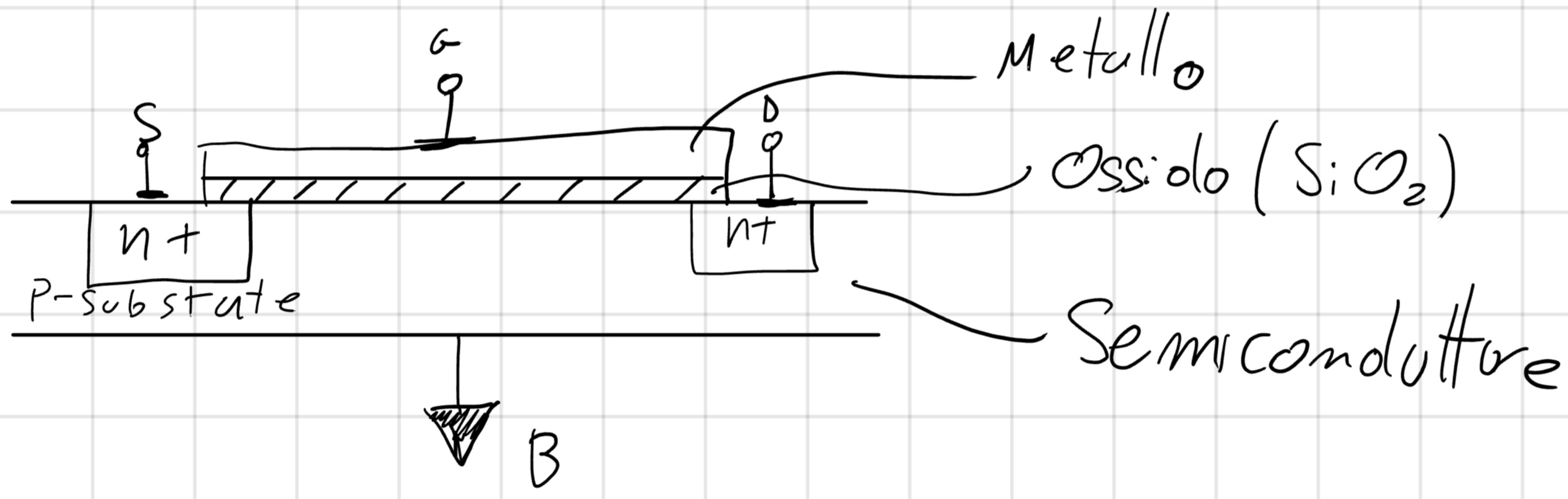
Dunque sul gate troviamo il metallo, poi ossido (spessore t_{ox}=1-10 nm) e il semiconduttore che nel PMOS è N, che come si può notare ha il compito di modulare la carica nel canale (sopra semiconduttore e sotto ossido).
Se hai capito il funzionamento del diodo, adorerai MOSFET Live, ehm… dicevo, se si è capito il diodo capire il FET sarà più semplice. Applicando una tensione positiva creiamo cariche negative libere che diventano fisse, (quindi NO corrente) il MOS è in interdizione, aumentando la tensione creo elettroni di conduzione, la tensione che crea elettroni di conduzione è settata ed è detta di soglia (threshold voltage, V_T), questa condizione viene chiamata inversione del canale (V_T=0,5V - 2V).
In parole povere più tensione applico più induco corrente (nella realtà prima o poi qualcosa fa “boom”).
Introduciamo ora le due regioni nel quale si può trovare un MOSFET: Ohmica e di Saturazione.
3.3 Regione Ohmica
Ci troviamo in questa regione quando la tensione applicata è molto piccola quindi abbiamo degli elettroni fissi ma non liberi (V_{DS} \to 0V).
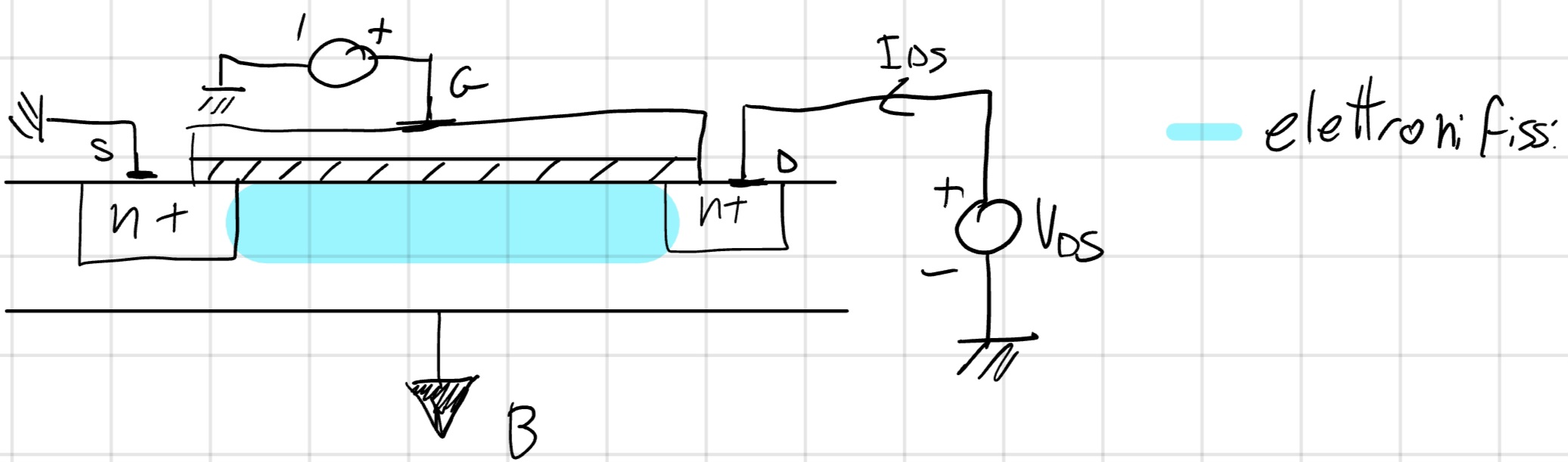
La carica libera presente (poca) nel canale dipende dalla tensione che sfora la V_T duqnue (V_{GS}-V_T) e dalla capacità dell’ossido C_{ox}(= \frac{\varepsilon_{ox}}{t_{ox}}WL) con W= larghezza e L= lunghezza:
Q_{CH}=C_{ox}(V_{GS}-V_T)
la velocità con il quale gli elettroni da source a drain dipende dal campo elettrico \implies V_{GS}:
v=\mu_n E=\mu_n \frac{V_{DS}}{L} con \mu_n = conduttività materiale.
La corrente è la carica spostata lungo L in un tempo secondo v:
I_{DS}=\frac{Q_{CH}}{\varDelta t}=\frac{Q_{CH}}{L/v}=\frac{C_{ox}(V_{GS}-V_T)}{\frac{L}{\mu_n \frac{V_{DS}}{L}}}=\frac{C_{ox}(V_{GS}-V_T)\mu_n V_{DS}}{L^2}
Per V_{DS} piccole il transistore (MOSFET) si comporta come una resistenza:
R_{CH}=\frac{V_{DS}}{I_{DS}}=\frac{L^2}{\mu_n C_{ox} (V_{GS} - V_T)}
Termini tecnici noiosi:
V_{GS}-V_T= Tensione di overdrive (V_{ov}).
\frac{W}{L}= fattore di forma.
Calcoli più precisi:
La densità superficiale di carica dipende non solo dalla tensione di Overdrive ma anche dalla tensione nel punto x del canale.
(se V_{DS} > 0) \implies Q'_{CH}=\frac{\varepsilon_{ox}}{t_{ox}}(V_{GS}-V_T-V(x))
La corrente (I_{DS}) è la carica superficiale (Q'_{CH}) integrata in W e x spostata in \varDelta t lungo L a v.
Q_{CH}=\int_{y=0}^{W} \int_{x=0}^{L} Q'_{CH}dxdy = \frac{WL}{V_{DS}}\int_{V(0)=0}^{V(L)=V_{DS}}Q'_{CH}dV(x) = \frac{WL}{V_{DS}} \frac{\varepsilon_{ox}}{t_{ox}}[(V_{GS}-V_T)V_{DS}-\frac{V_{DS}^2}{2}]
I_{DS} = \frac{Q_{CH}}{\varDelta t} = \mu_n \frac{\varepsilon_{ox}}{t_{ox}} \frac{W}{L} (V_{GS}- V_T-\frac{V_{DS}}{2})V_{DS} = \mu_n C_{ox} (V_{GS}-V_T-\frac{V_{DS}}{2})V_{DS}
R_{CH}(V_{DS}) = \frac{\partial V_{DS}}{\partial I_{DS}} = \frac{L^2}{\mu_n C_{ox}(V_{GS}-V_T-V_{DS})}
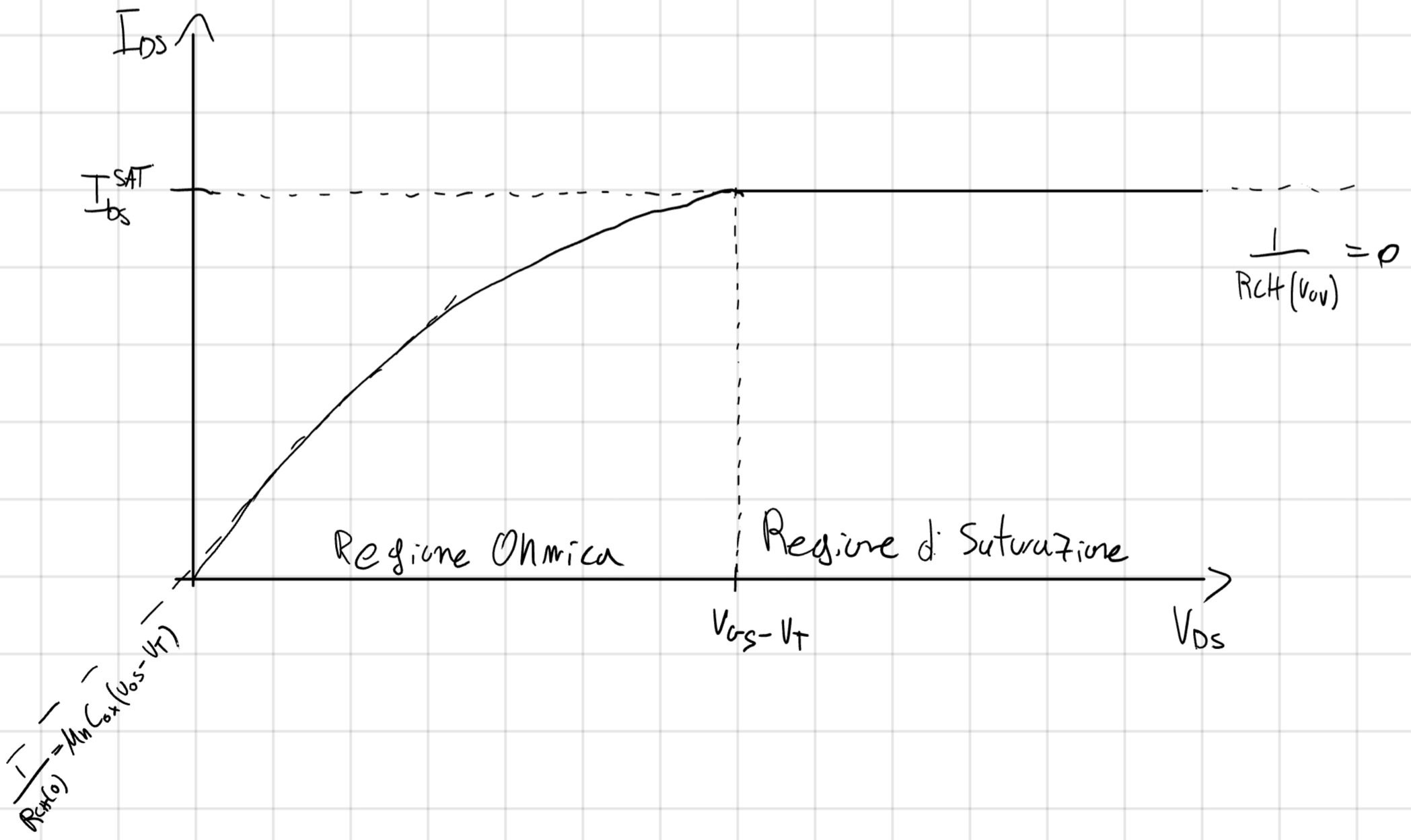
3.4 Regione di Staurazione
Quando V_{DS} raggiunge la tensione Overdrive l’aumento di tensione non apporta alcuna modifica questo stato si chiama Regione di Saturazione, il MOS si comporta come un generatore di corrente.
I_{DS}^{SAT}=I_{DS}V_{DS} \implies I_{DS}^{SAT}= \frac{1}{2} \mu_n C_{ox} (V_{GS}-V_T)^2
Nella realtà l’aumento di tensione aumenta la corrente di un fattore \lambda, non più generatore ideale:
I_{DS}^{SAT}= \frac{1}{2} \mu_n C_{ox} (V_{GS}-V_T)^2 (1+ \lambda V_{DS})
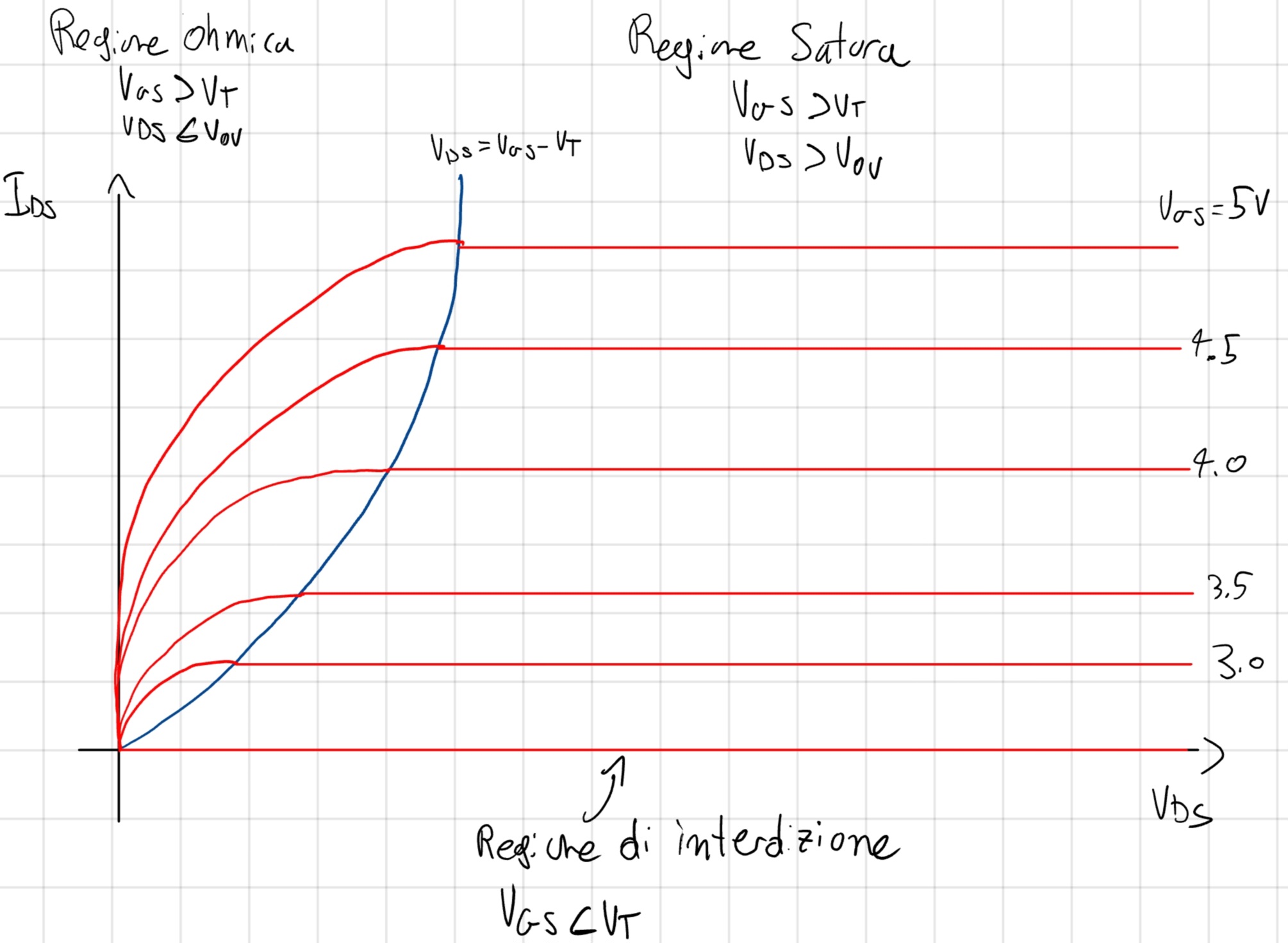
3.5 Formule
- NMOS
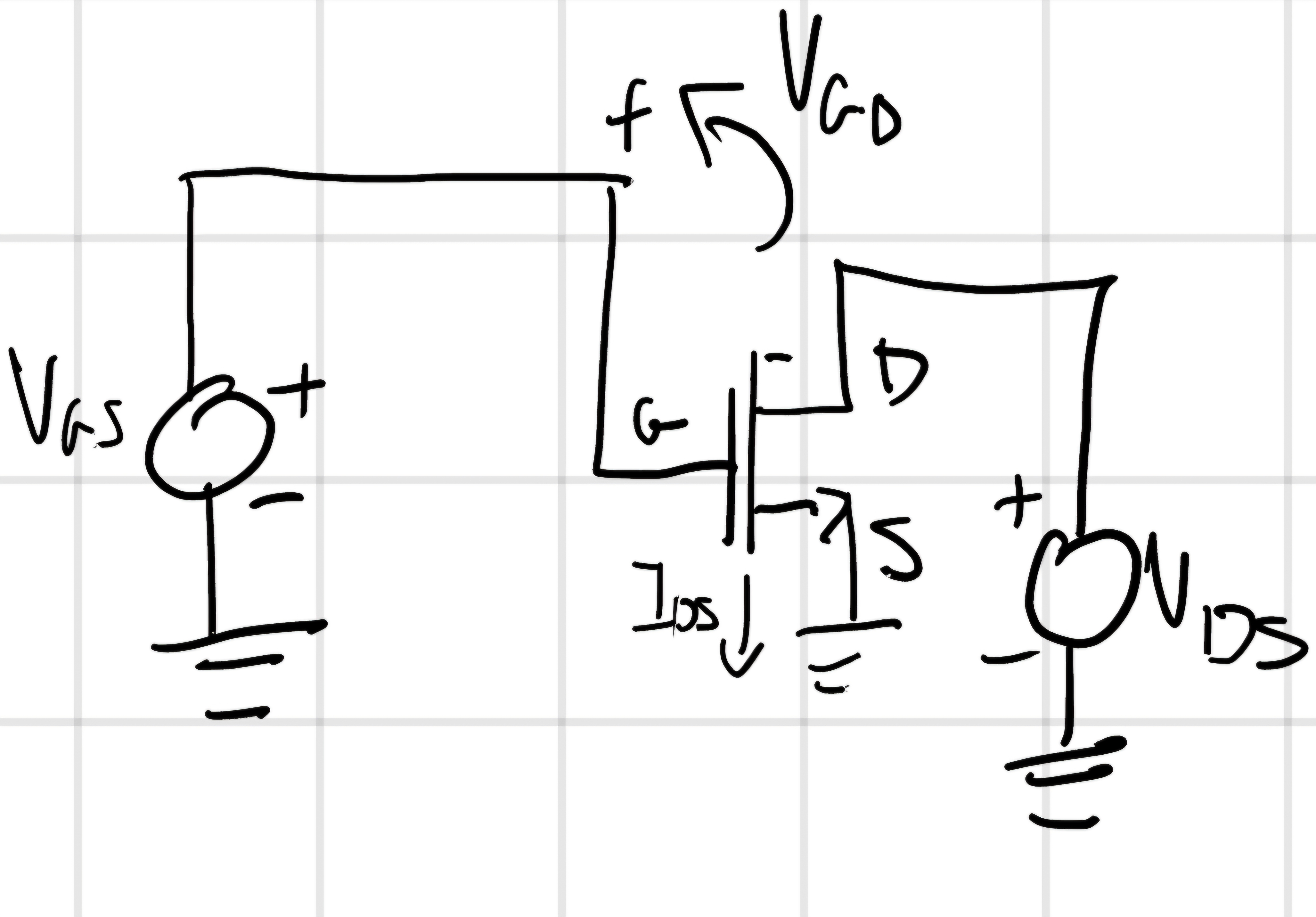
SATURAZIONE
V_{GS}>V_T>0
V_{DS}>V_{ov}
I_{DS}^{SAT}= \frac{1}{2} \mu_n C_{ox} (V_{GS}-V_T)^2>0
OHMICA
V_{GS} > V_T
V_{DS} < V_{ov}
I_{DS} = \mu_n C_{ox} (V_{GS} - V_T - \frac{V_{DS}}{2}) V_{DS} > 0
INTERDIZIONE
V_{GS} < V_T
I_{DS} = 0
PMOS
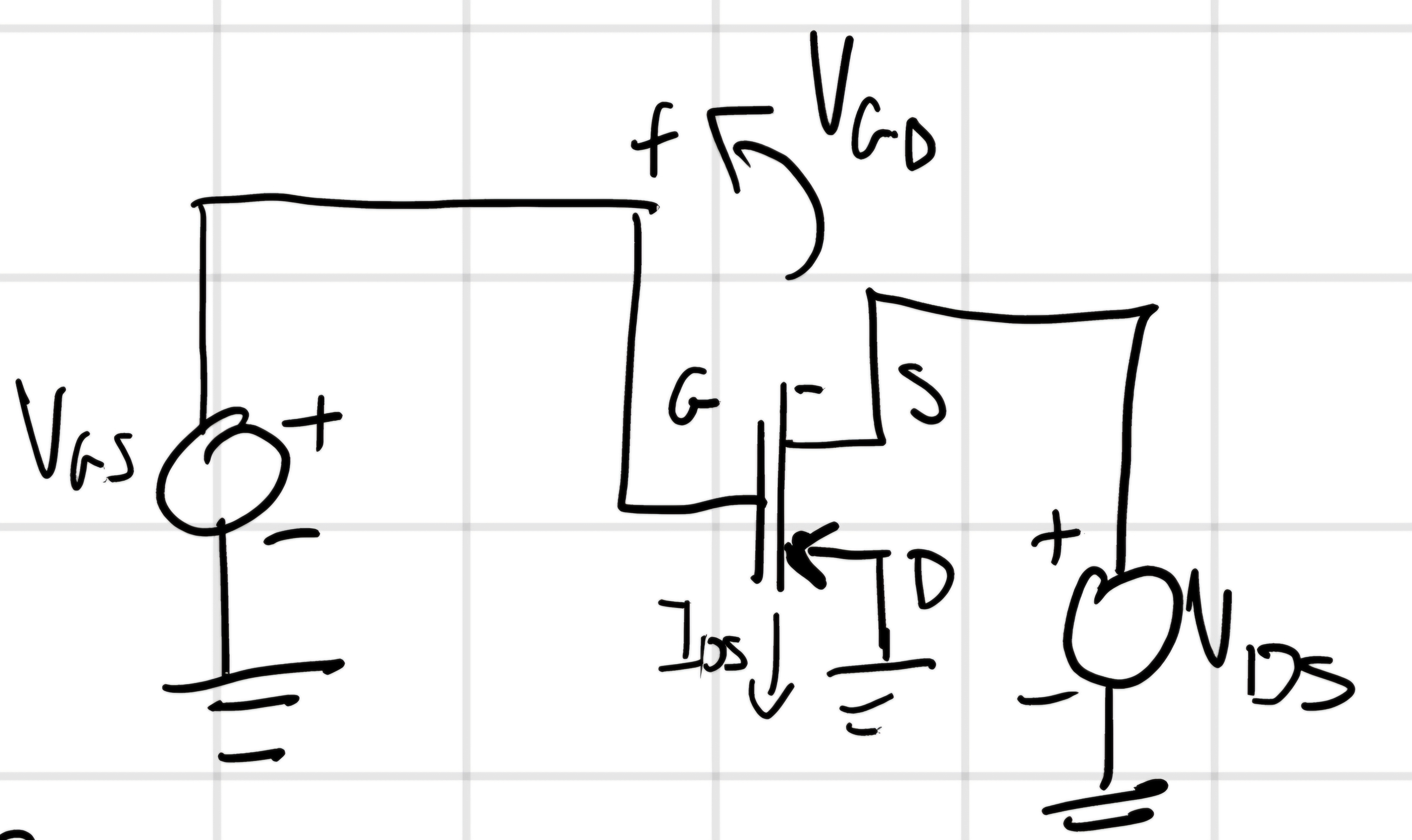
SATURAZIONE
V_{GS} < V_T < 0
V_{DS} < V_{ov}
I_{DS}^{SAT}= - \frac{1}{2} \mu_p C_{ox} (V_{GS} - V_T)^2 < 0
OHMICA
V_{GS}<V_T
V_{DS} > V_{ov}
I_{DS} = - \mu_p C_{ox} (V_{GS} - V_T - \frac{V_{DS}}{2}) V_{DS} < 0
INTERDIZIONE
V_{GS} < V_T
I_{DS} = 0
3.6 Curiosità finali
I MOS sono ottimi interrutori visto che si comportano da circuiti aperti quando V_{GS} < V_T ( V_{GS} < |V_T| per PMOS ) e da resistenza quando V_{GS} > V_T ( V_{GS} > |V_T| per PMOS ).
Se ho MOS in serie la K_{eq} = \frac{1}{K_{eq}}= \Sigma_1^n \frac{1}{K_i}, in parallelo K_{eq}= \Sigma_1^n K_i.
Capitolo Quattro: Analisi Circuitale pt.2
4.1 Caratteristiche circuitali logiche
D’ora in avanti ci troveremo davanti svariate parole che indicano determinate caratteristiche dei circuiti logici, qui potevo decidere di spiegarli la prima volta che si usavano ma ho deciso che è meglio avere un elenco dove ci sono tutte, ecco cosa vogliono dire;
Caratteristica (statica) Ingresso/Uscita: Uscita in funzione degli ingressi.
Soglia logica: Tensione che divide 0 e 1 logico.
Livelli logici: Livelli di tensione che determinano 0 e 1 logico.
Noise Margin: Massima fluttuazione tollerabile sul livello logico.
Tempo di propagazione: Tempo che ci mettono i segnali ad arrivare nelle varie parti del circuito.
Potenza dissipata:
- Statica: Devo davvero spiegarlo ?
- Dinamica: Idem con patate.
Area: Spazio occupato.
Fan-Out: Numero massimo di device pilotabili senza perdita di informazioni.
Capitolo Cinque: Logica CMOS
Come abbiamo detto nel capitolo tre i MOS sono ottimi interruttori che hanno due funzioniamenti distinti: pull-up (PU) e pull-down (PD) con PD forziamo un livello “low” (L) in uscita mentre con PU un livello “high” (H) in uscita.
I PMOS sono ottimi interruttori con PU mentre gli NMOS sono ottimi interruttori con PD.
5.1 PDN e PUN
Cambio formule:
Per K_n si intende K_n = \frac{1}{2} \mu_n C_{ox} mentre con K_p = \frac{1}{2} \mu_p C_{ox}
Per i PMOS in Ohmica si usa anche I_{SD} = 2 K_p (V_{SG} - |V_T| - \frac{V_{SD}}{2})V_{SD} e la satuta I_{SD}^{SAT} = K_p (V_{SG} - |V_T|)^2.
Cambio rappresentazione:
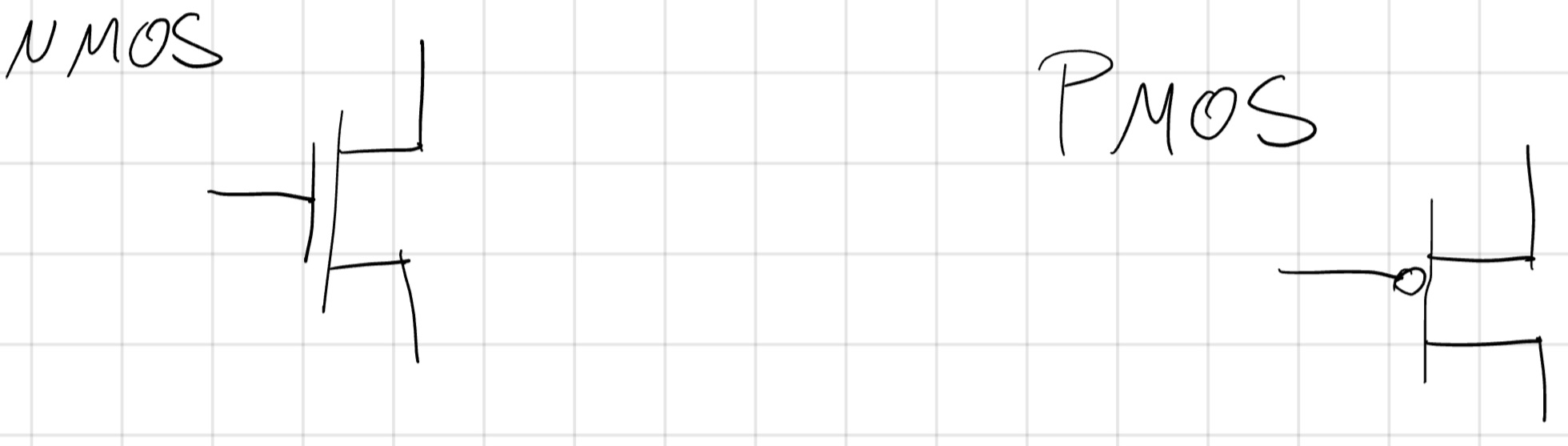
NMOS PDN
- Portano corrente tra D ed S
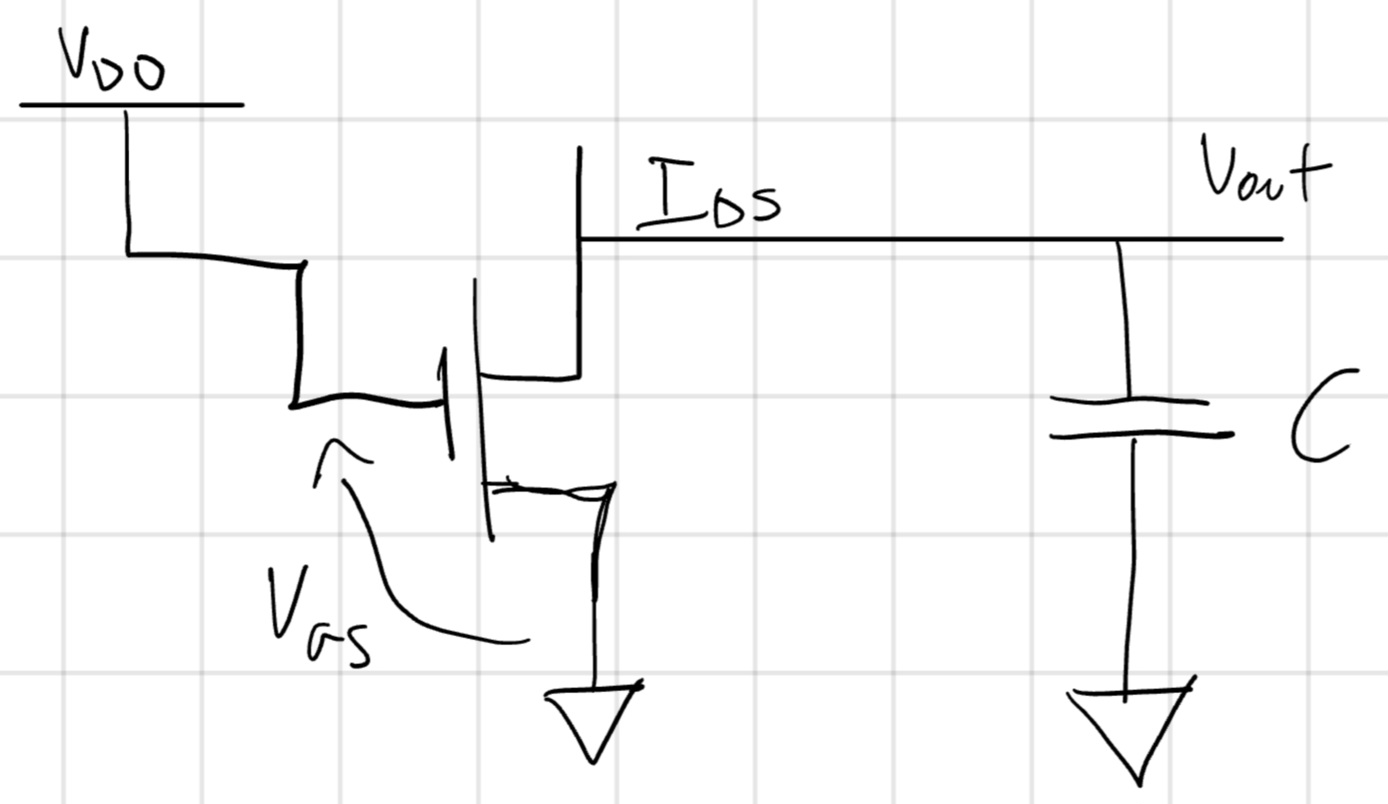
Per digitalizzarlo bisogna pilotare l’NMOS:
- G dell’NMOS a V_{DD}.
- Tengo i S più vicini a GROUND.
Una rete di NMOS con PD si chiama PDN (Pull-down Network).
PMOS PUN
- Spingono una corrente da S a D
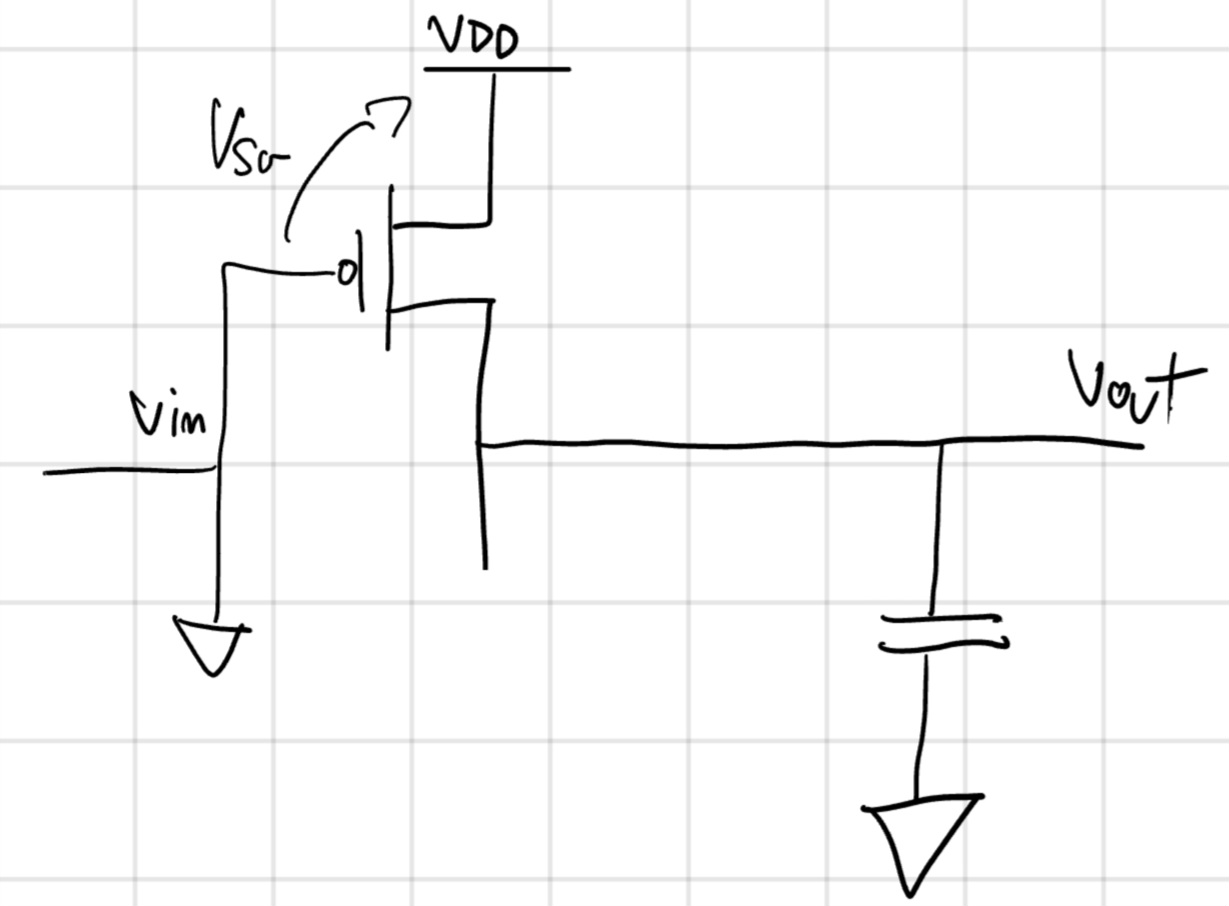
Per digitalizzarlo bisogna pilotare il PMOS:
- G a 0.
- S vicino a V_{DD}
Una rete di PMOS con PU si parla di PUN (Pull-up Network).
5.2 F-CMOS
La logica fully complementary MOS (F-CMOS) serve per realizzare parte con PUN e PDN che lavorano in mutua esclusione.
Proprietà:
- Potenza statica nulla.
- V_{OH} = V_{DD} e V_{OL} = GND
- Fronte di salita (t_R) e discesa (t_F) dei segnali d’ingresso, creando cross-conduzione (P_{CROSS} \propto t_{R/F}).
5.3 Porte logiche
In questo paragrafo parleremo di due porte logiche NAND-2 e NOR-2 analizzandone in/out e caratteristiche elettroniche.
NAND-2
Y=\neg(AB)
| A | B | Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
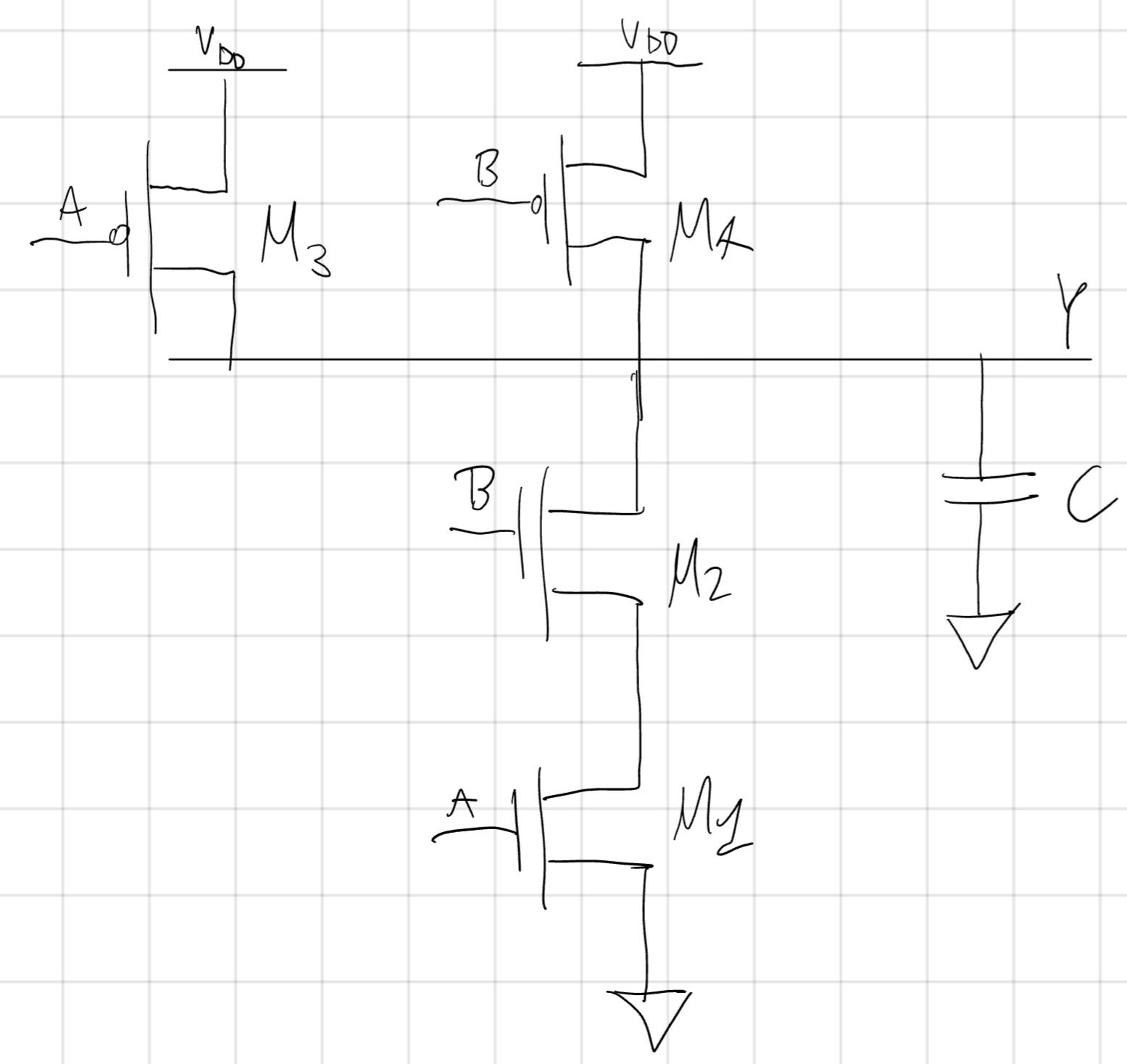
Abbiamo 3 effetti IN/OUT dipende da come commutano A e B, con 3 inverter si ha:
- AB(00) \to AB(11)
- AB(10) \to AB(11)
- AB(01) \to AB(11)
Ogni “caratteristica” avrà punti caratteristici diversi, ma sempre V_{OH} = V_{DD} e V_{OL} = GND.
In tutti i casi useremo il seguente circuito:
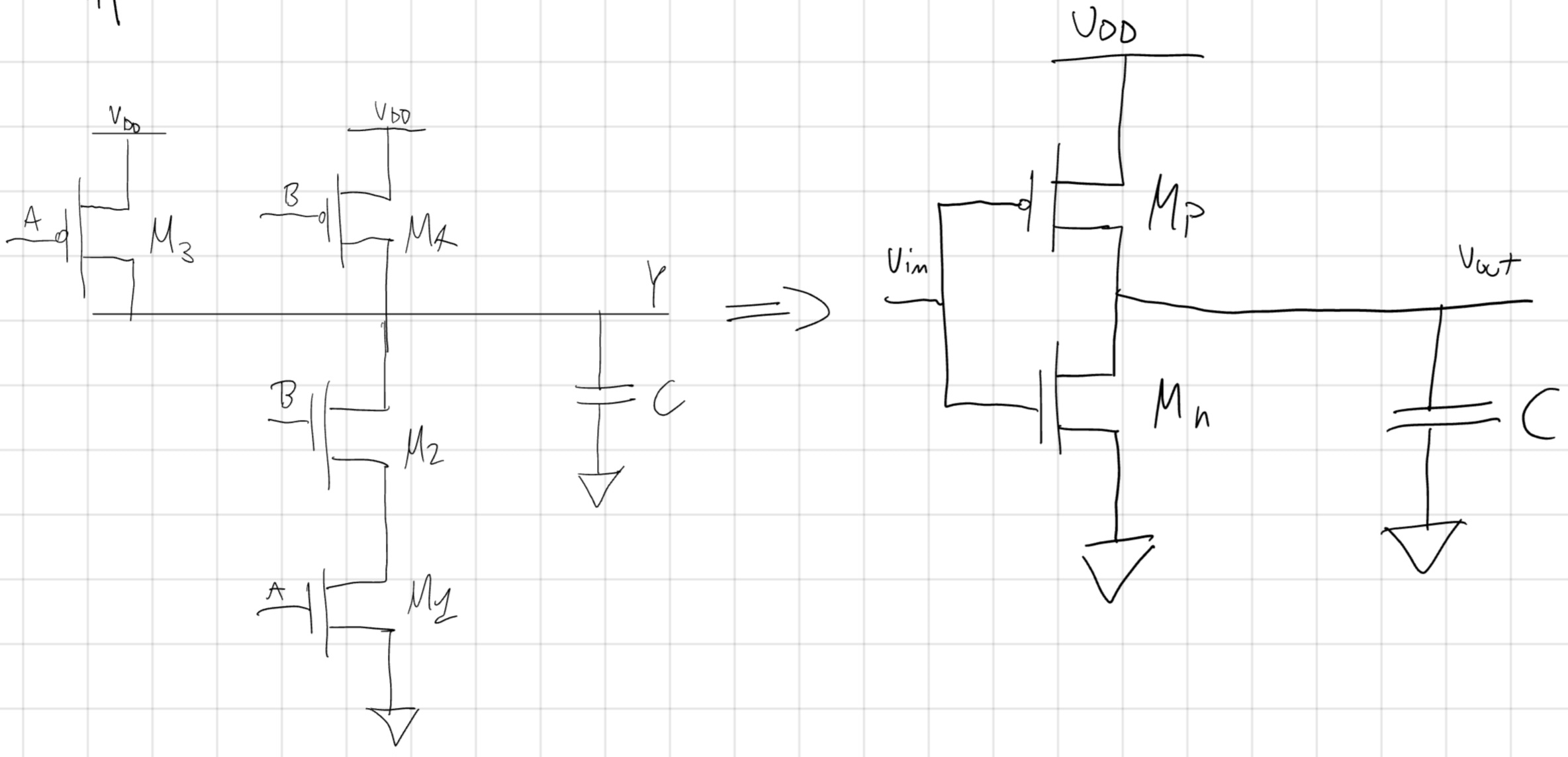
- AB(00) \to AB(11)
AB(00): \\M_3 ed M_4 ON.
M_1, M_2 OFF.
AB(11) : \\ M_3, M_4 OFF.
M_1, M_2 ON.
K_{M_p} = K_3 + K_4
K_{M_n} = \frac{K_1 K_2}{K_1 + K_2}
Tempi di propagazione:
t_{p,LH}^{11,00} = C \frac{V_M - V_{OL}}{K_{M_n}(V_{DD} - V_T)^2} = C \frac{V_M}{(K_3 + K_4)(V_{DD} - V_T)^2}
t_{p,HL}^{00,11} = C \frac{V_{OH} - V_M}{ K_{M_p}(V_{DD} - V_T)^2} = C \frac{V_{DD} - V_M}{\frac{K_1 K_2}{K_1+ K_2} (V_{DD} - V_T)^2}
- AB(01) \to AB(11)
AB(01): \\M_3 ON ed M_4 OFF.
M_1 OFF M_2 ON.
AB(11) : \\ M_3, M_4 OFF.
M_1, M_2 ON.
K_{M_p} = K_3
K_{M_n} = \frac{K_1 K_2}{K_1 + K_2}
Tempi di propagazione:
t_{p,LH}^{11,01} = C \frac{V_M - V_{OL}}{K_{M_n}(V_{DD} - V_T)^2} = C \frac{V_M}{K_3(V_{DD} - V_T)^2}
t_{p,HL}^{01,11} = C \frac{V_{OH} - V_M}{ K_{M_p}(V_{DD} - V_T)^2} = C \frac{V_{DD} - V_M}{\frac{K_1 K_2}{K_1+ K_2} (V_{DD} - V_T)^2}
- AB(10) \to AB(11)
AB(10): \\M_3 OFF ed M_4 ON.
M_1 ON M_2 OFF.
AB(11) : \\ M_3, M_4 OFF.
M_1, M_2 ON.
K_{M_p} = K_4
K_{M_n} = \frac{K_1 K_2}{K_1 + K_2}
Tempi di propagazione:
t_{p,LH}^{11,10} = C \frac{V_M}{K_4(V_{DD} - V_T)^2}
t_{p,HL}^{10,11} = C \frac{V_{DD} - V_M}{\frac{K_1 K_2}{K_1+ K_2} (V_{DD} - V_T)^2}
NOR-2
Y = \neg (A+B)
| A | B | Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
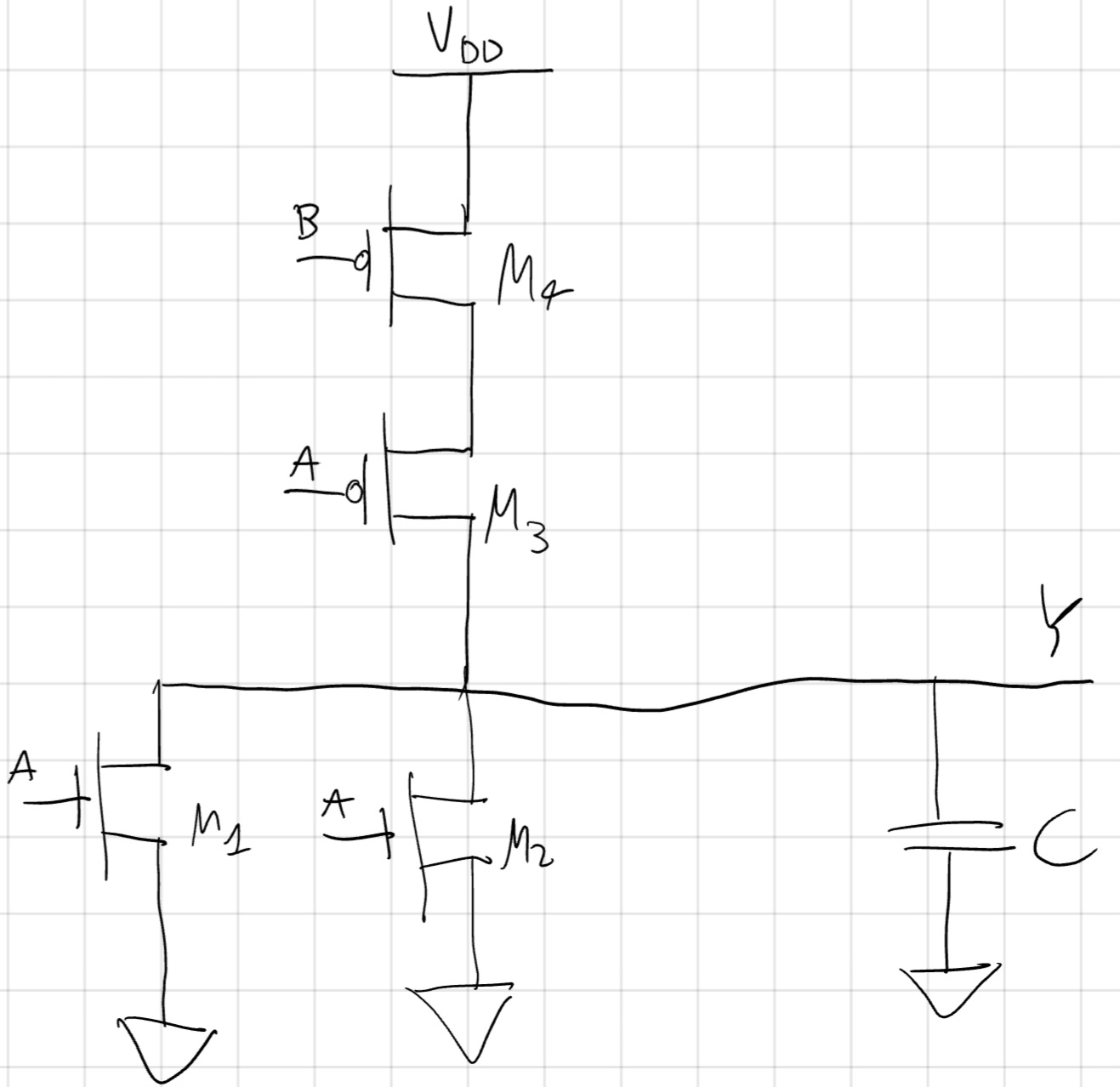
3 Caratteristiche IN/OUT:
- AB(00) \to AB(11)
- AB(00) \to AB(01)
- AB(00) \to AB(10)
con sempre V_{OH} = V_{DD} e V_{OL} = GND.
Useremo come prima il seguente circuito:
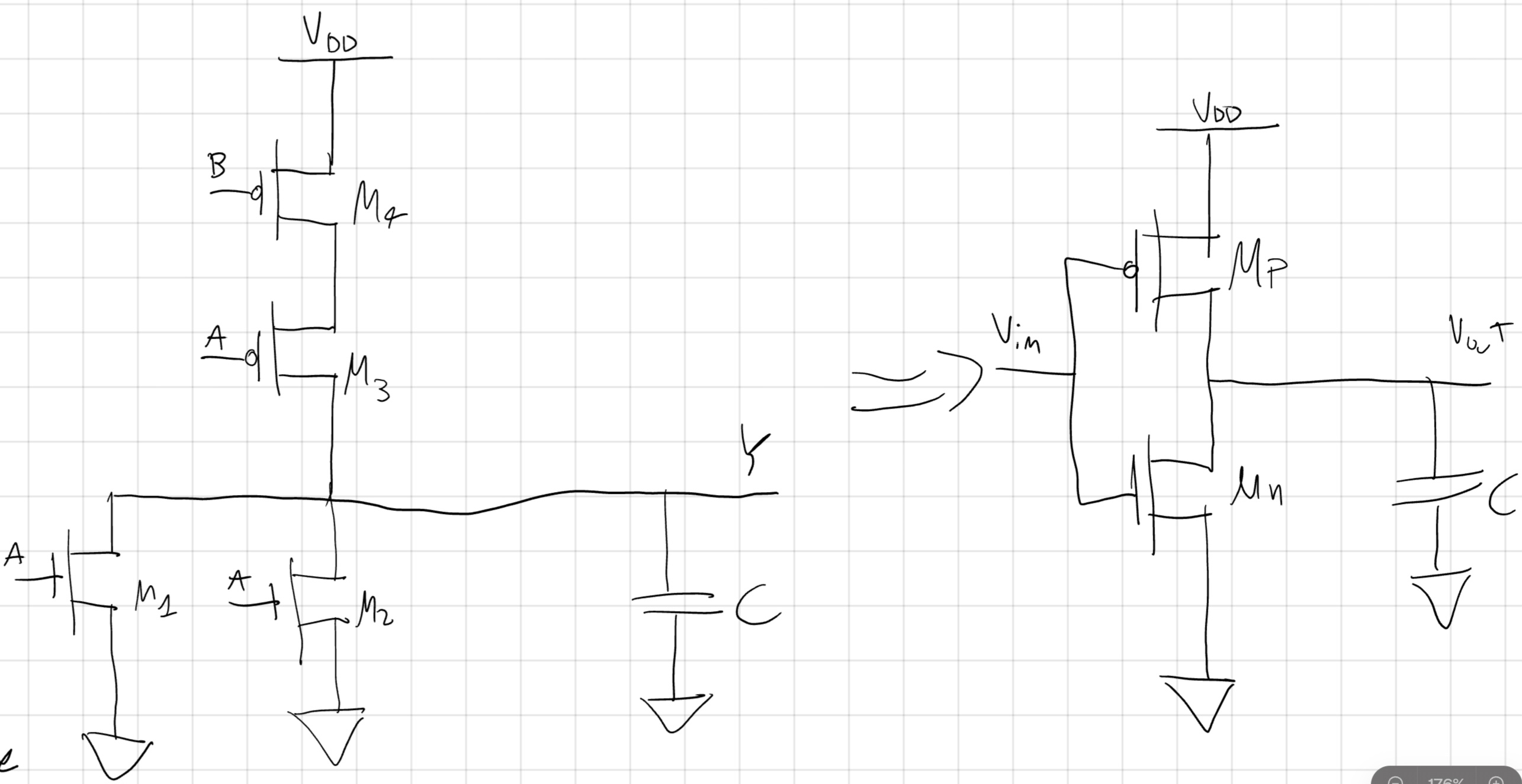
- AB(00) \to AB(11)
AB(00): \\M_3 ed M_4 ON.
M_1 ed M_2 OFF.
AB(11) : \\ M_3, M_4 OFF.
M_1, M_2 ON.
K_{M_p} = \frac{K_3 K_4}{K_3 + K_4}
K_{M_n} = K_1 + K_2
Tempi di propagazione:
t_{p,LH}^{11,00} = C \frac{V_M}{\frac{K_3 K_4}{K_3 + K_4}(V_{DD} - V_T)^2}
t_{p,HL}^{00,11} = C \frac{V_{DD} - V_M}{(K_1 + K_2)(V_{DD} - V_T)^2}
- AB(00) \to AB(01)
AB(00): \\M_3 ed M_4 ON.
M_1 ed M_2 OFF.
AB(01) : \\ M_3 ON M_4$ OFF.
M_1 OFF M_2$ ON.
K_{M_p} = \frac{K_3 K_4}{K_3 + K_4}
K_{M_n} = K_2
Tempi di propagazione:
t_{p,LH}^{01,00} = C \frac{V_M}{\frac{K_3 K_4}{K_3 + K_4}(V_{DD} - V_T)^2}
t_{p,HL}^{00,01} = C \frac{V_{DD} - V_M}{K_2(V_{DD} - V_T)^2}
- AB(00) \to AB(10)
AB(00): \\M_3 ed M_4 ON.
M_1 ed M_2 OFF.
AB(10) : \\ M_3 OFF M_4$ ON.
M_1 ON M_2$ OFF.
K_{M_p} = \frac{K_3 K_4}{K_3 + K_4}
K_{M_n} = K_1
Tempi di propagazione:
t_{p,LH}^{00,10} = C \frac{V_M}{\frac{K_3 K_4}{K_3 + K_4}(V_{DD} - V_T)^2}
t_{p,HL}^{10,00} = C \frac{V_{DD} - V_M}{K_1(V_{DD} - V_T)^2}
Caratteristiche Elettroniche sinstesi (Reti logiche ma a FdE, anche loro presenti su appunti).
CMOS offre:
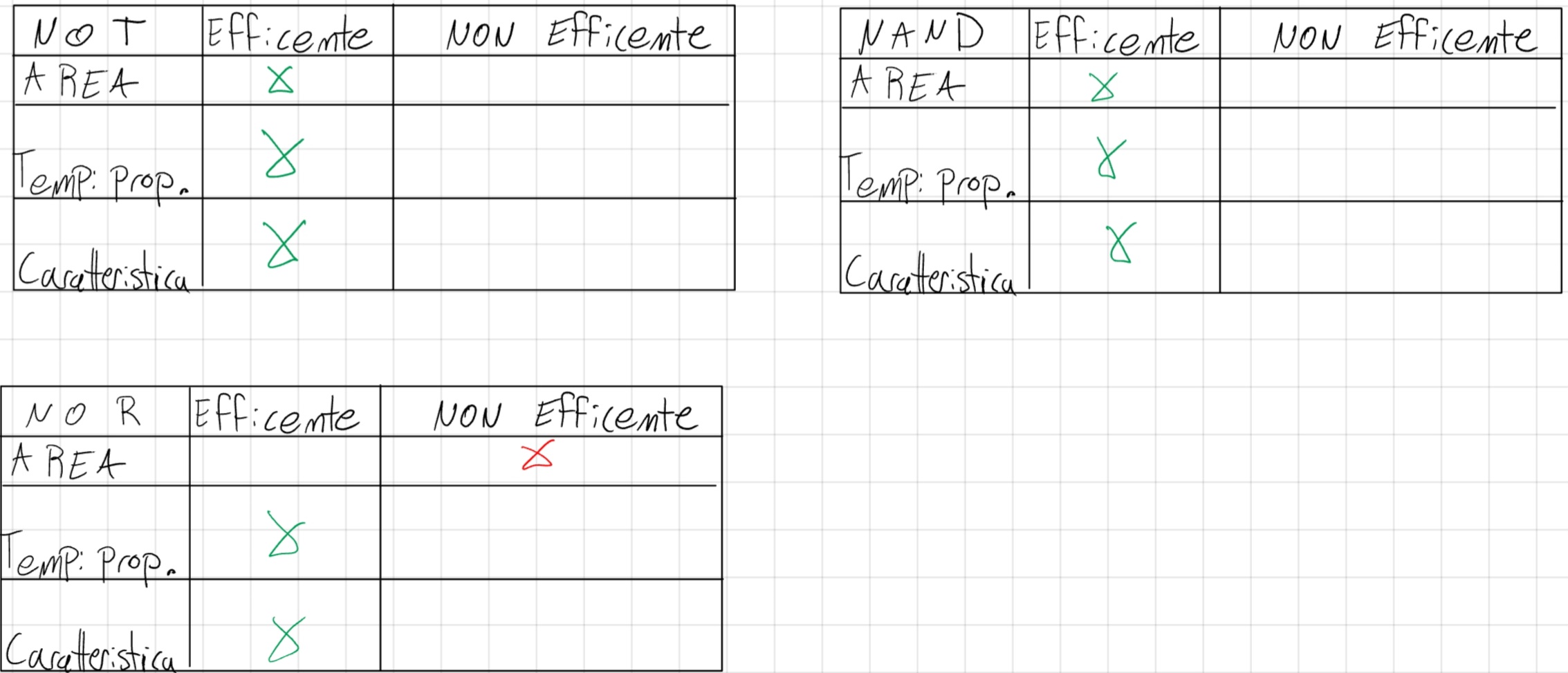
Il resto sono tecniche di espansione delle formule logiche, consigliamo la visione di “Reti Logiche” presente su appunti.
5.4 Porte NMOS e PMOS
Problematiche CMOS:
- Perdita di capacità di corrente dovuta ai MOS in serie.
- Aumento Area per bilanciare questo.
- Aumento di MOS = aumento capacità di carica C_{ox}' (= \frac{\varepsilon_{ox}}{t_{ox}}) ed area totale della porta.
- Un grande C_L = aumento potenza dinamica.
- Grandi capacità parassite riducono frontesalita e discesa aumento di cross-conduzione.
Porte NMOS
Sostituisco (con dei costi che vedremo) le PUN con resistori o PMOS accesi.
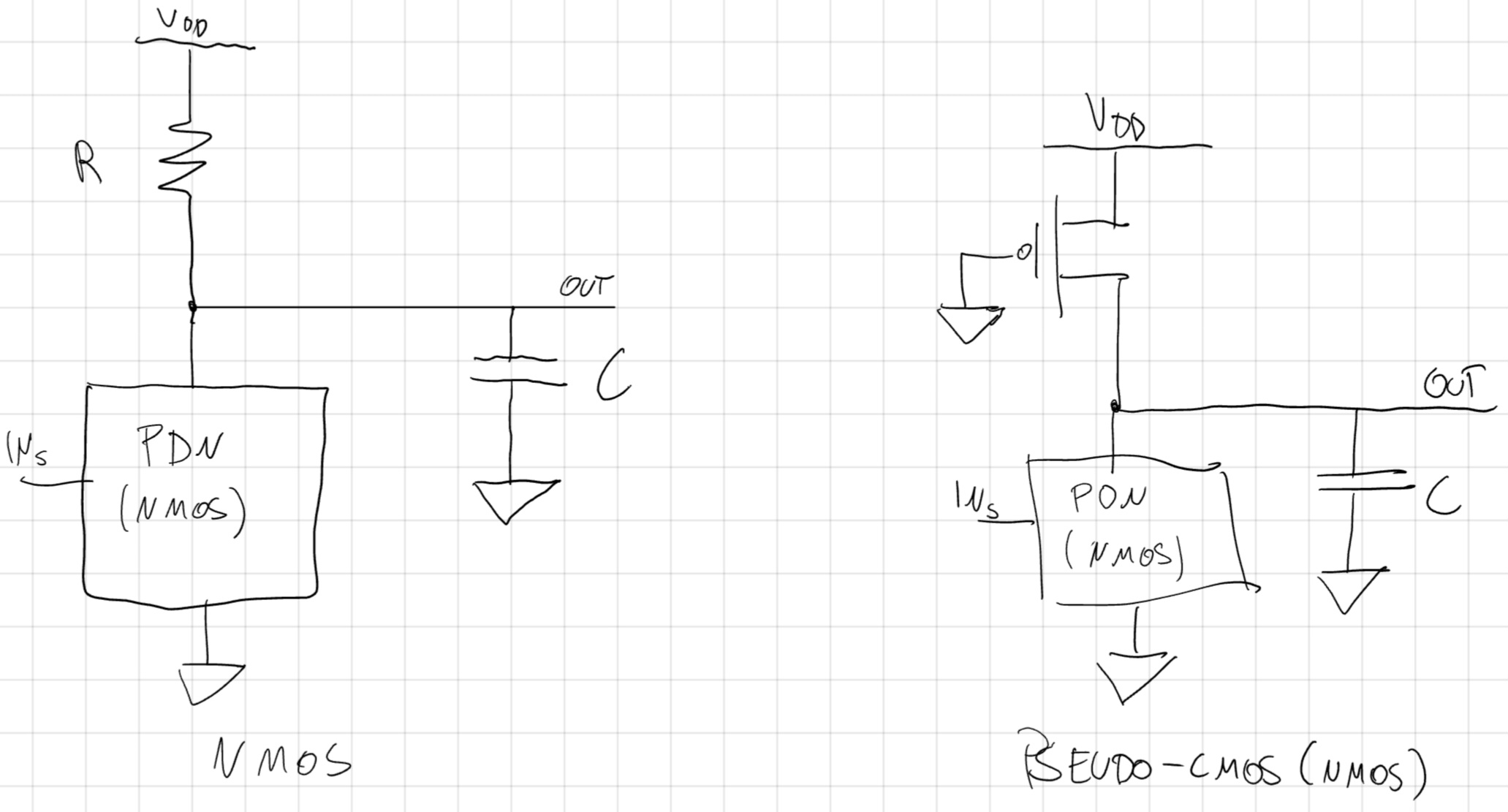
Costi:
- Potenza dissipata statica non nulla.
- V_{OH} = V_{DD} ma V_{OL} > GND
- t_{p, HL}^{INs} dipende dal K dell’NMOS eq., se trascuriamo R e PMOS.
- t_{p,LH}^{INs} dipende solo dal K del PMOS o dal RC.
Porte PMOS
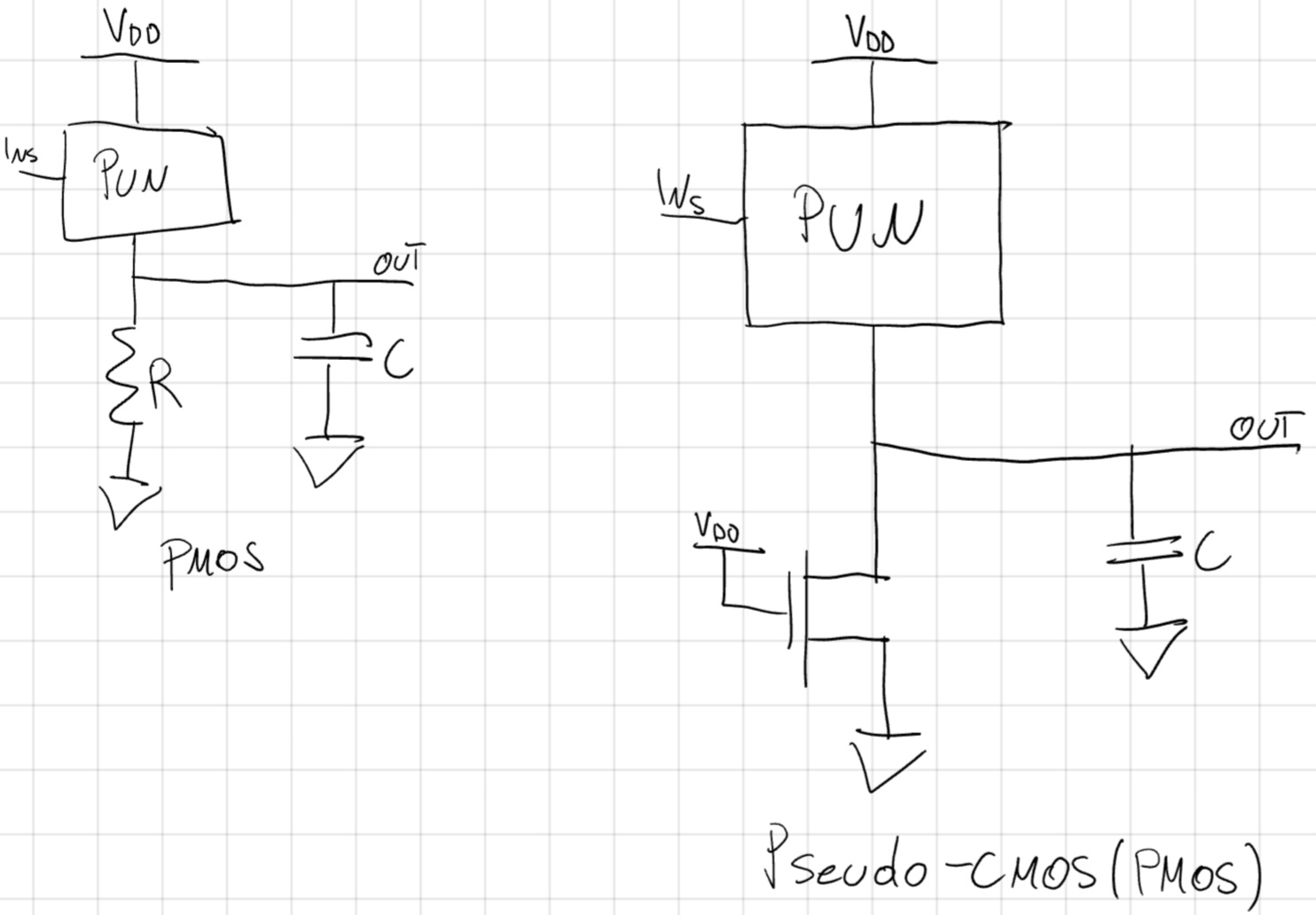
Costi:
- Potenza dissipata non nulla.
- V_{OL} = GND ma V_{OH} < V_{DD}.
- t_{p,HL}^{INs} dipendono solo da K del NMOS o RC.
- t_{p,LH}^{INs} dipendono da K_{eq} PUN, se trascuriamo R e NMOS.
5.5 Porte (C)MOSTri-State
In questo tipo di porte oltre a 1 e 0 abbiamo l’alta impedenza (HZ), in questo stato i dispositivi incaricati del PU e PD vengono spenti (o sconnessi) lasciando l’uscita flottante.
L’ingresso se acceso fa tutto normalmente altrimenti lascia l’output a HZ.
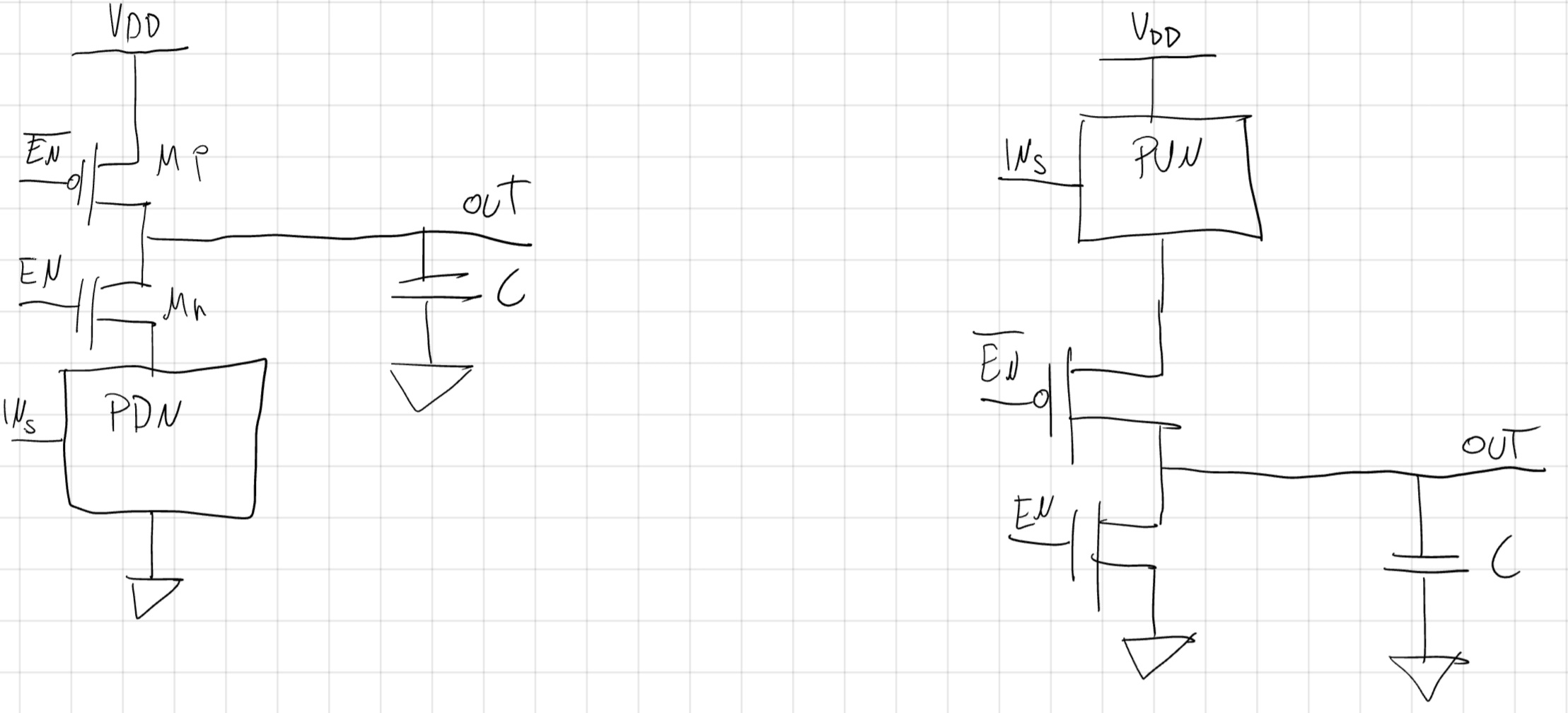
Svantaggi:
- Aumento Area.
- Poichè bisogna raddoppiare la dimensione dei MOS per stesso t_p.
- MOS E_n grossi almeno quanto K_{eq} PUN e PDN.
- \neg E_n si genera con NOT su E_n.
- Più parassiti = meno t_p e più potenza dinamica.
- Viene usata solo raramente.
Capitolo Sei: Logiche PT e TG
Lookup Table (LUT), tipo di memoria ROM, banale MUX.
LUT n-to-m
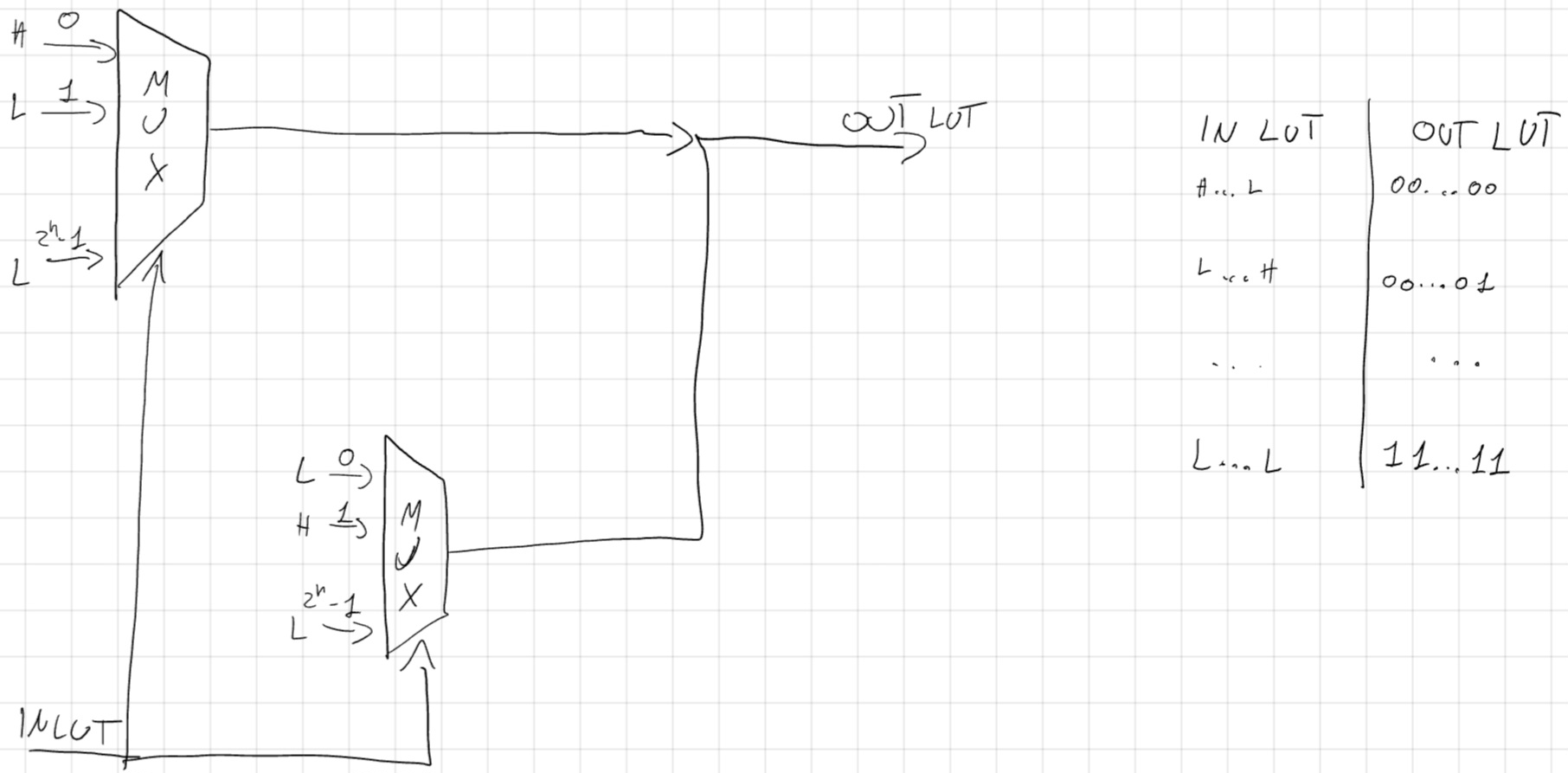
Come costruiamo un MUX ?
- Porte CMOS (poco efficiente).
- Logica Pass Transistor (PT) o Transfer Gate (TG), questo metodo è più efficiente.
6.1 Pass Transistor Logic (PTL)
La PTL usa i MOS come interrutori sul percorso digitale per realizzare dei MUX.
N.B. Nei PTL si utilizza un solo tipo di MOS ed è preferibile che sia un NMOS.
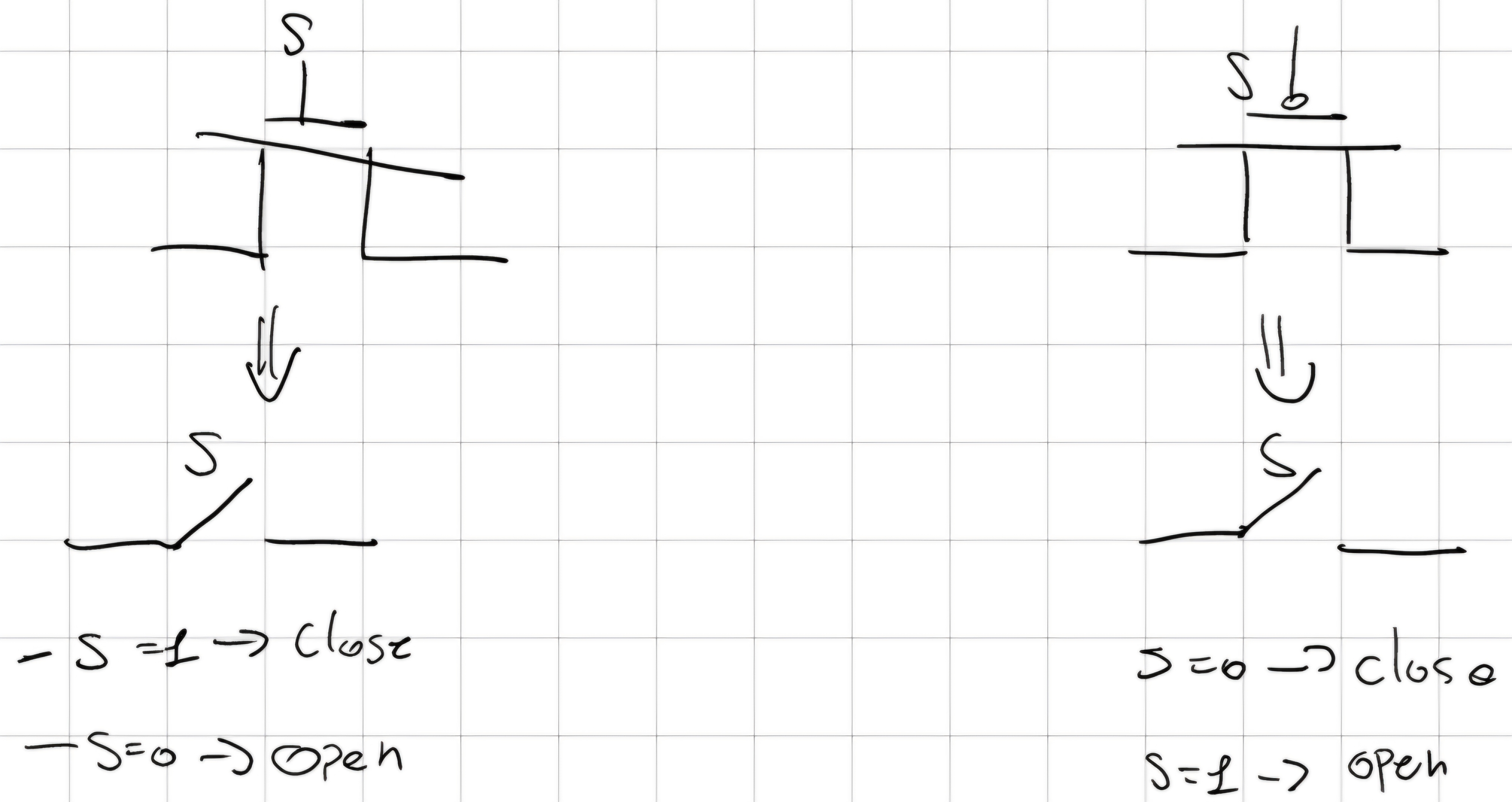
MUX 2-to-1
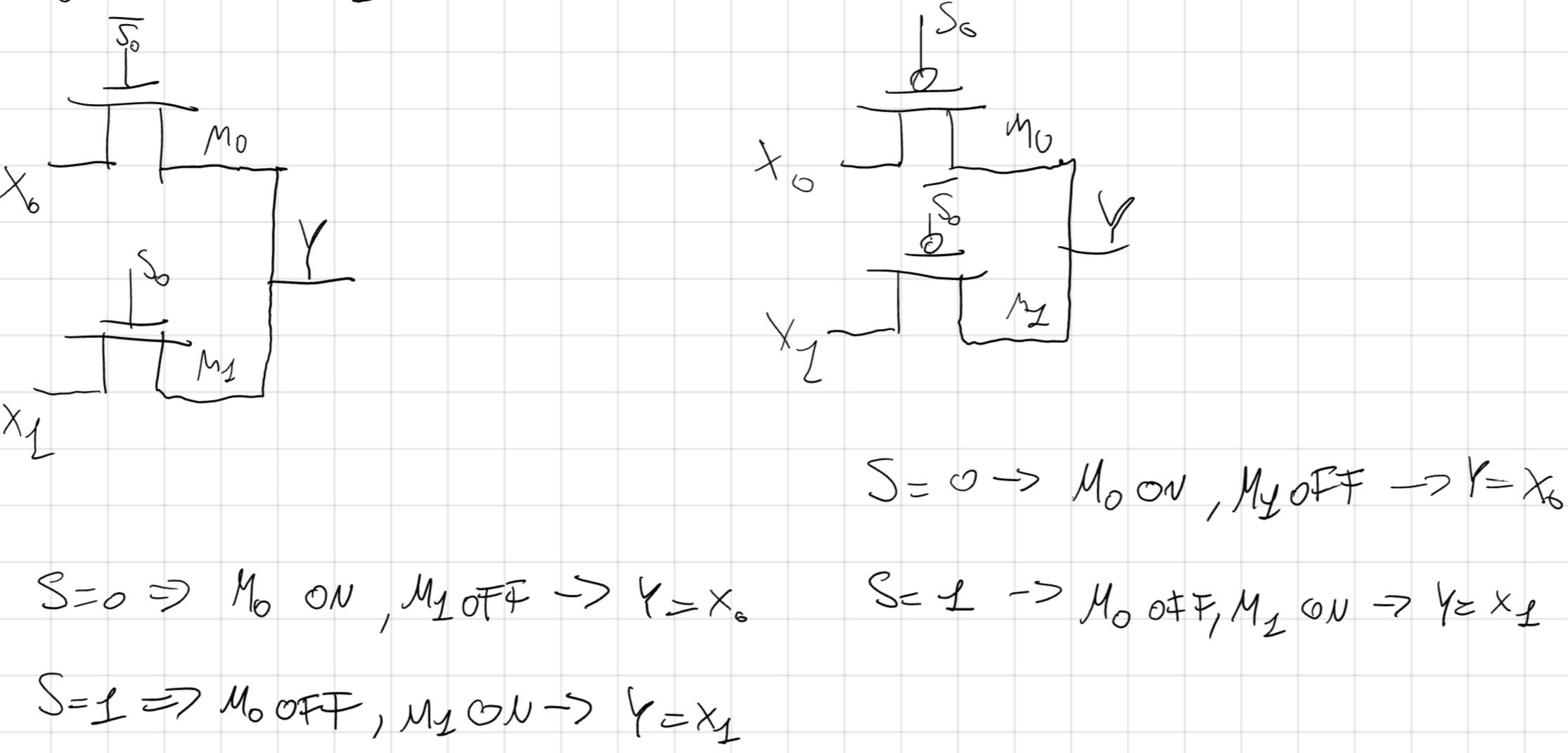
Per un generico 2^n MUX:
- Y = X(n).
- Si compone come un albero di MUX 2-to-1.
- Per ogni S_i bisogna avere un inverter \neg S_i.
6.2 Porte logiche e parassitismi
AND-2
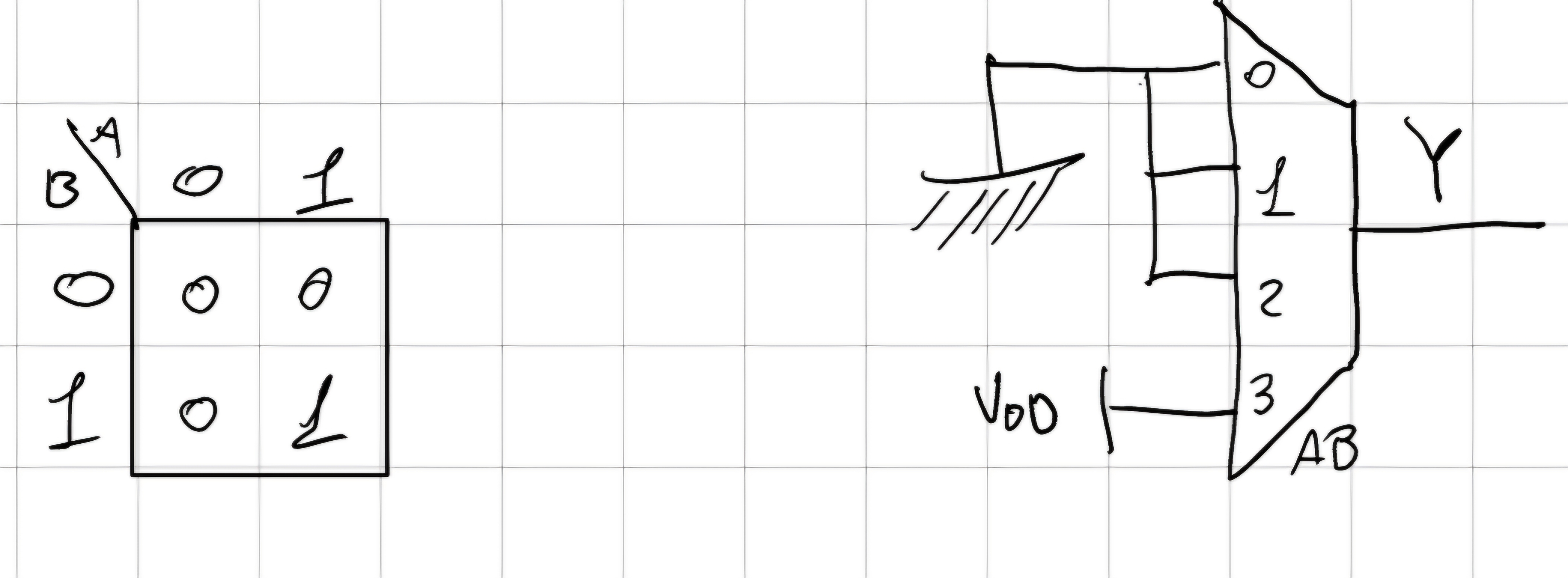
Riduzione
Ci rediamo conto che quando A=0 \to Y=0 mentre A=1 \to Y=B.
Quindi:
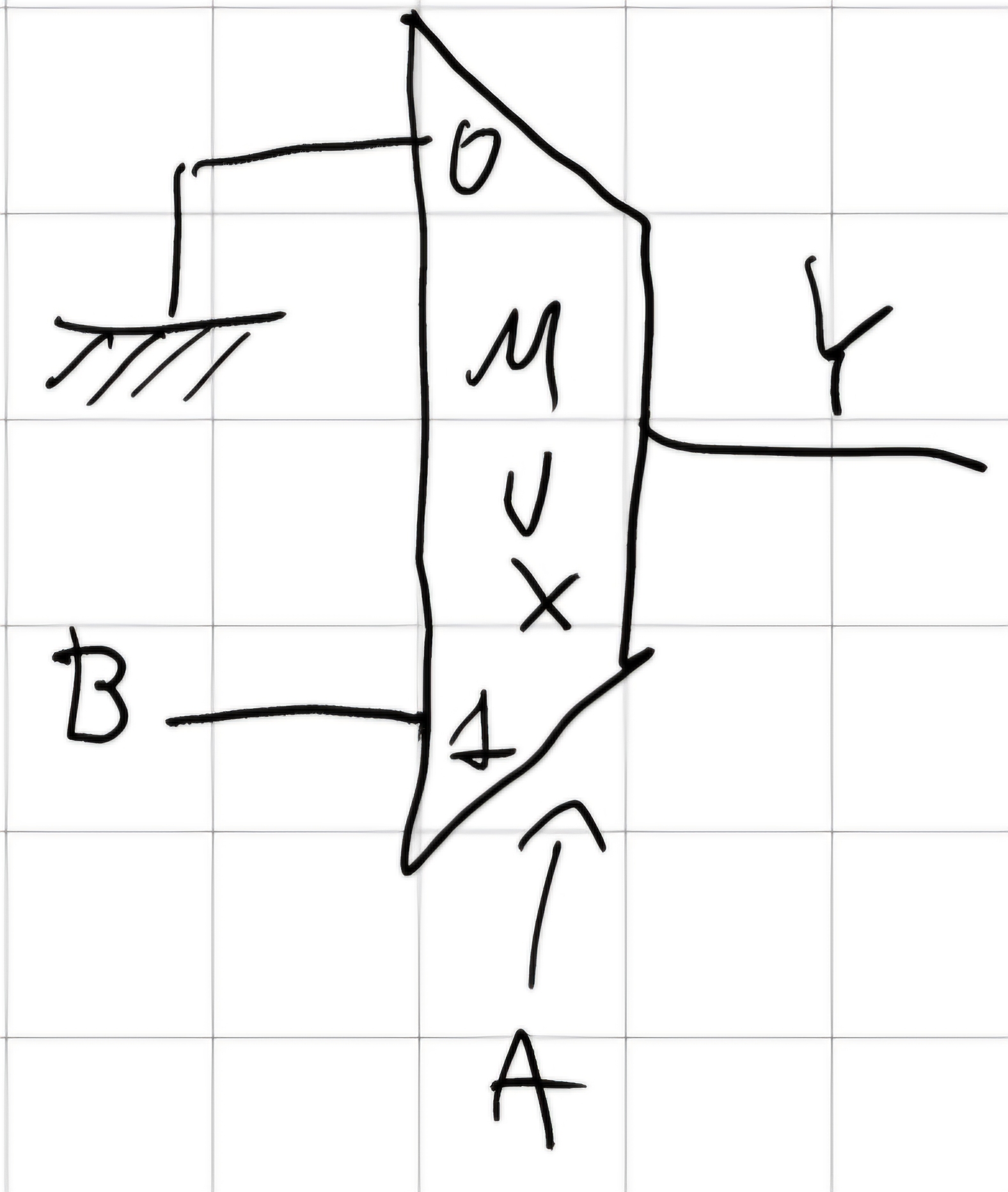
OR-2
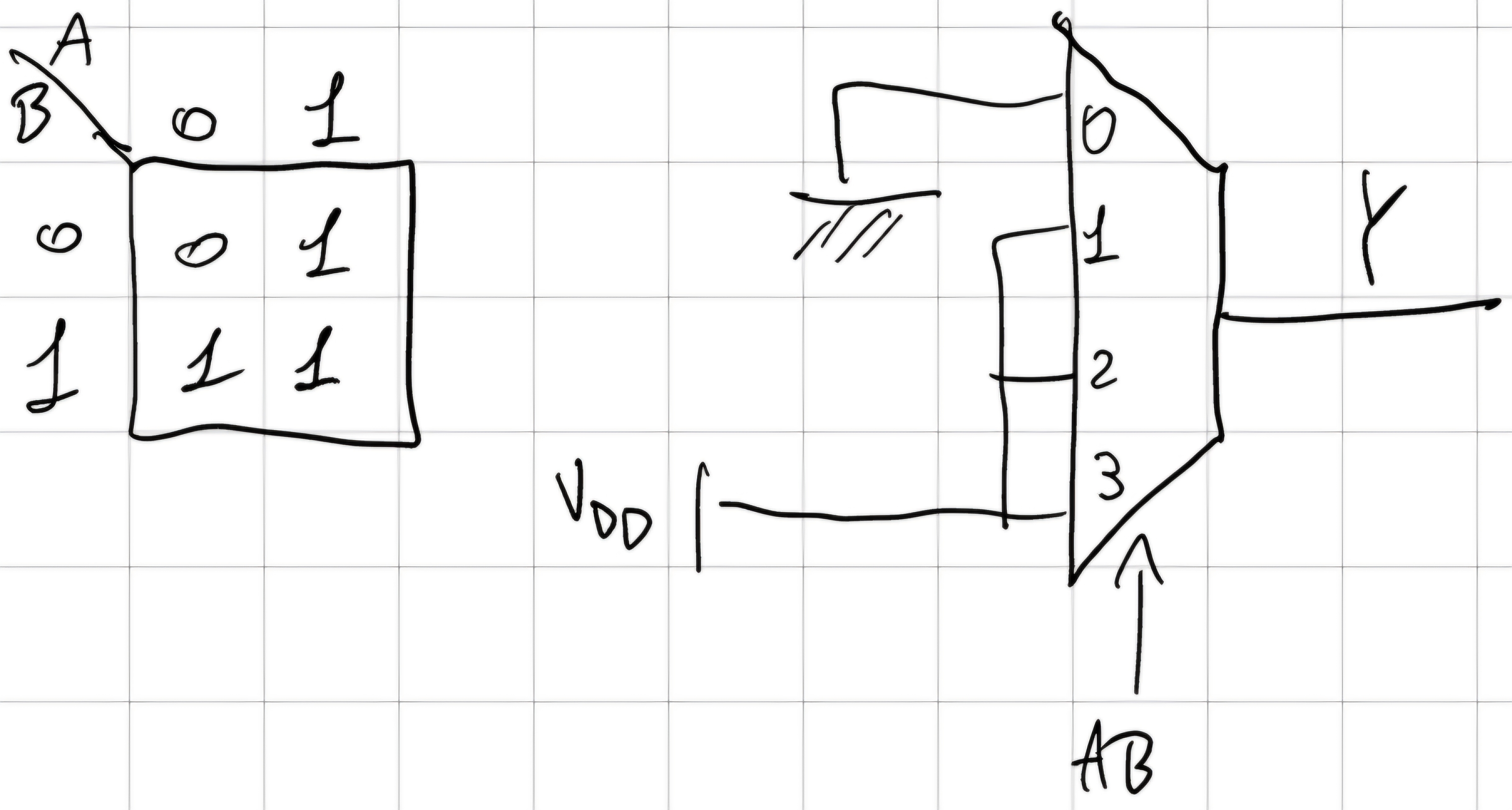
Riduzione
Notiamo che se A=1 \to Y=1 se A=0 \to Y=B quindi:
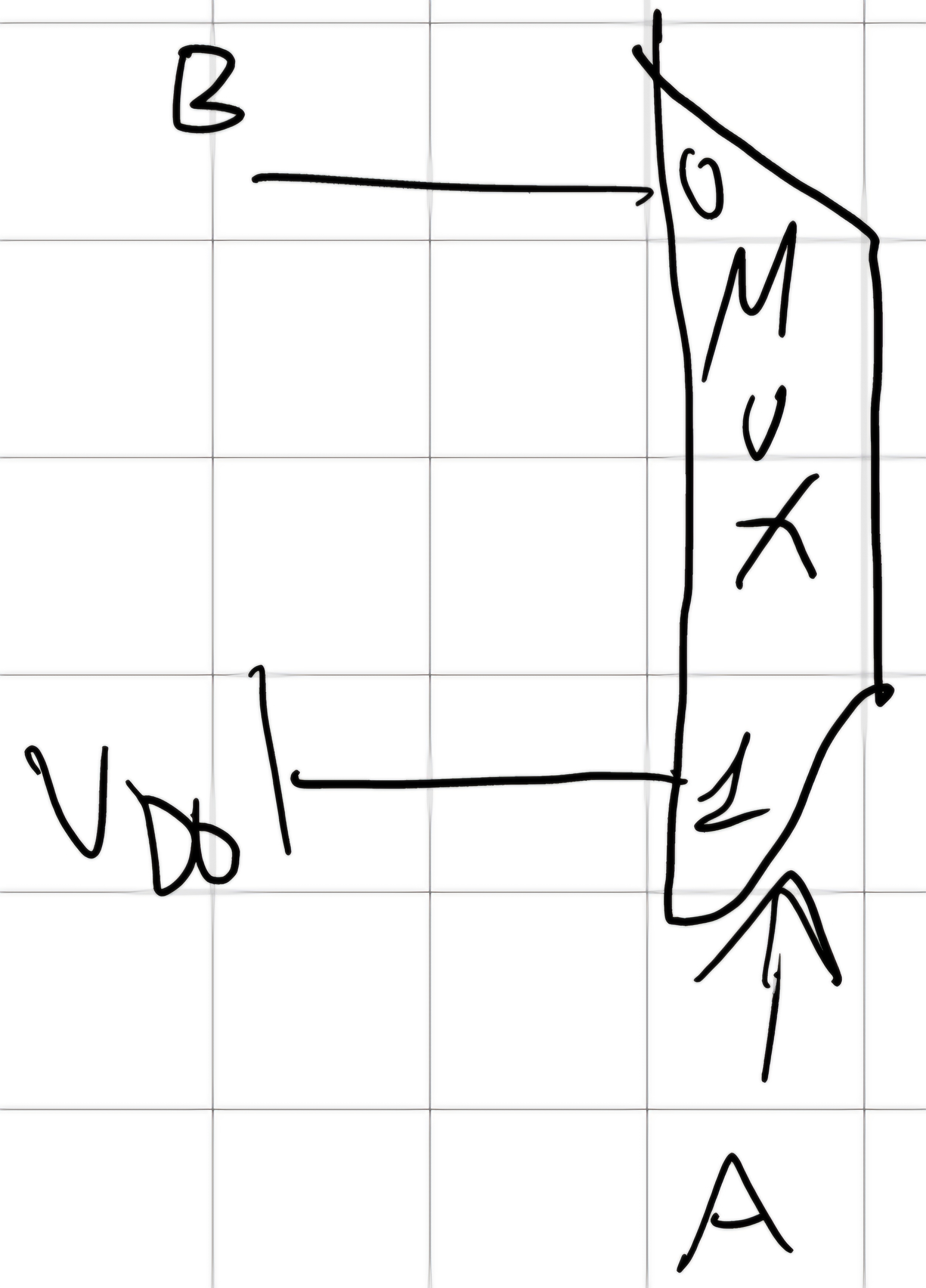
Parassitismo
A causa del condensatore MOS, possono nascere anche nei PTL capacità parassite.
N.B. Noi NON siamo in grado di calcolare le capacità parassite da solo \implies sono date dal testo.
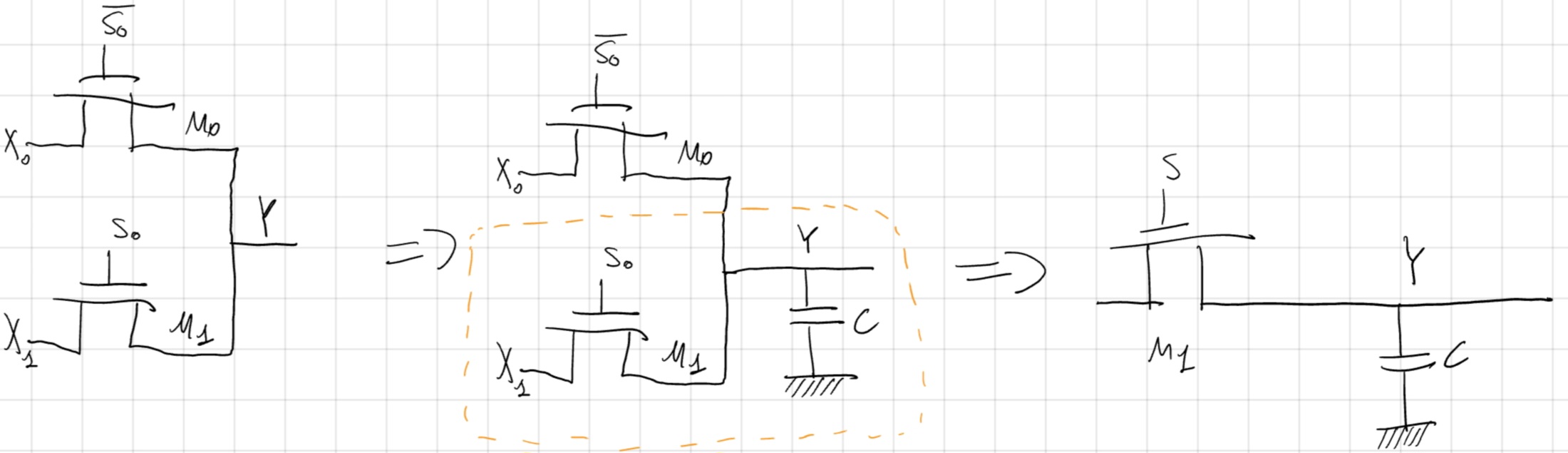
6.3 Cariche e Scariche MOS
NMOS
Scarica H \to L
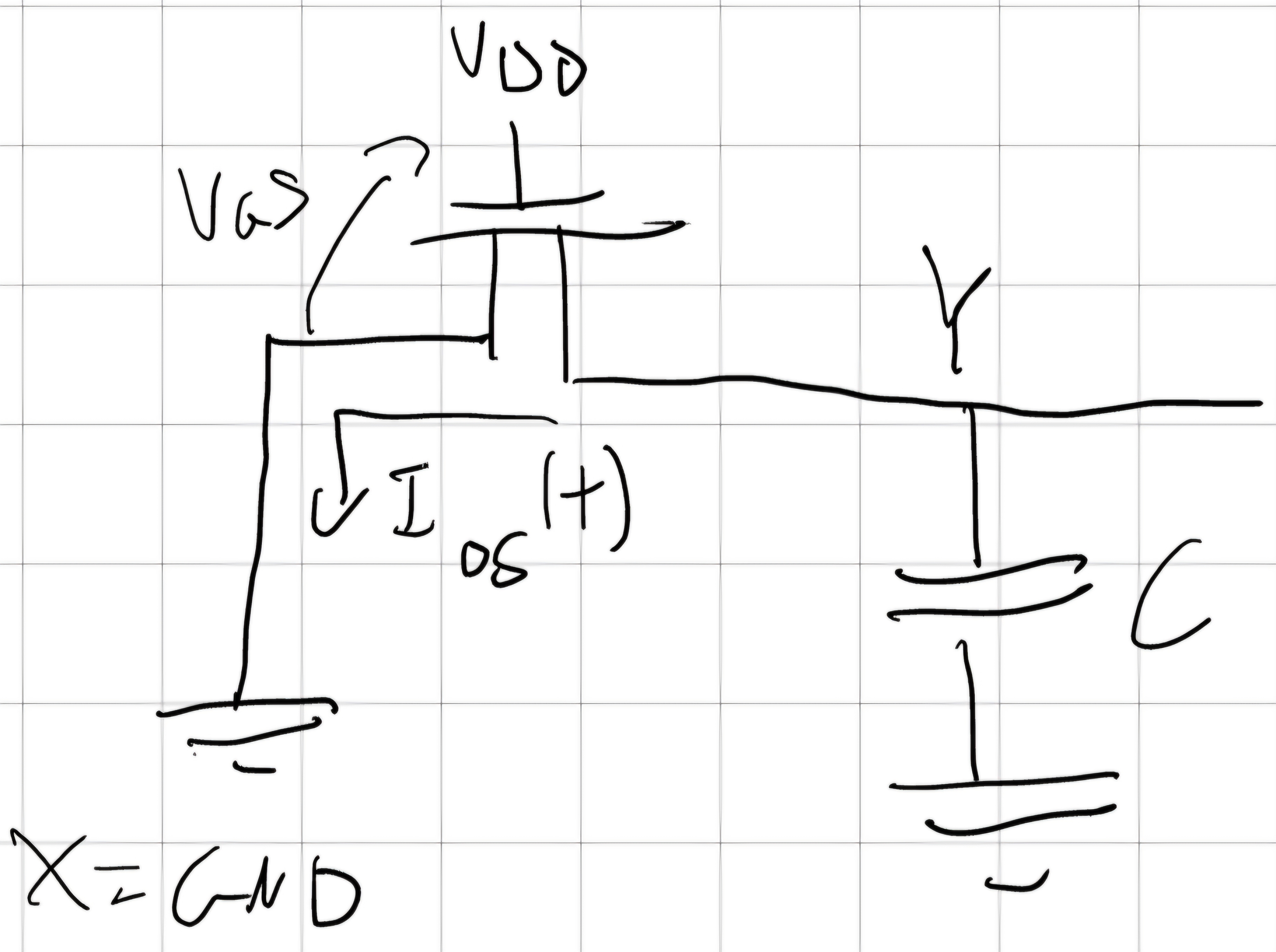
Fino a Y=V_{ov} scarica in saturazione, dopo in ohmica fino a GND.
I_{ds}(t) = -i_c (t) \\ I_{DS} (t) = -\frac{dY(t)}{dt} \\ t_{p,HL} = t_{p,HL}^{SAT} + t_{p,HL}^{OHM} \\ t_{p,HL} \cong \frac{C \varDelta Y}{K_n V_{ov}^2}
Carica L \to H
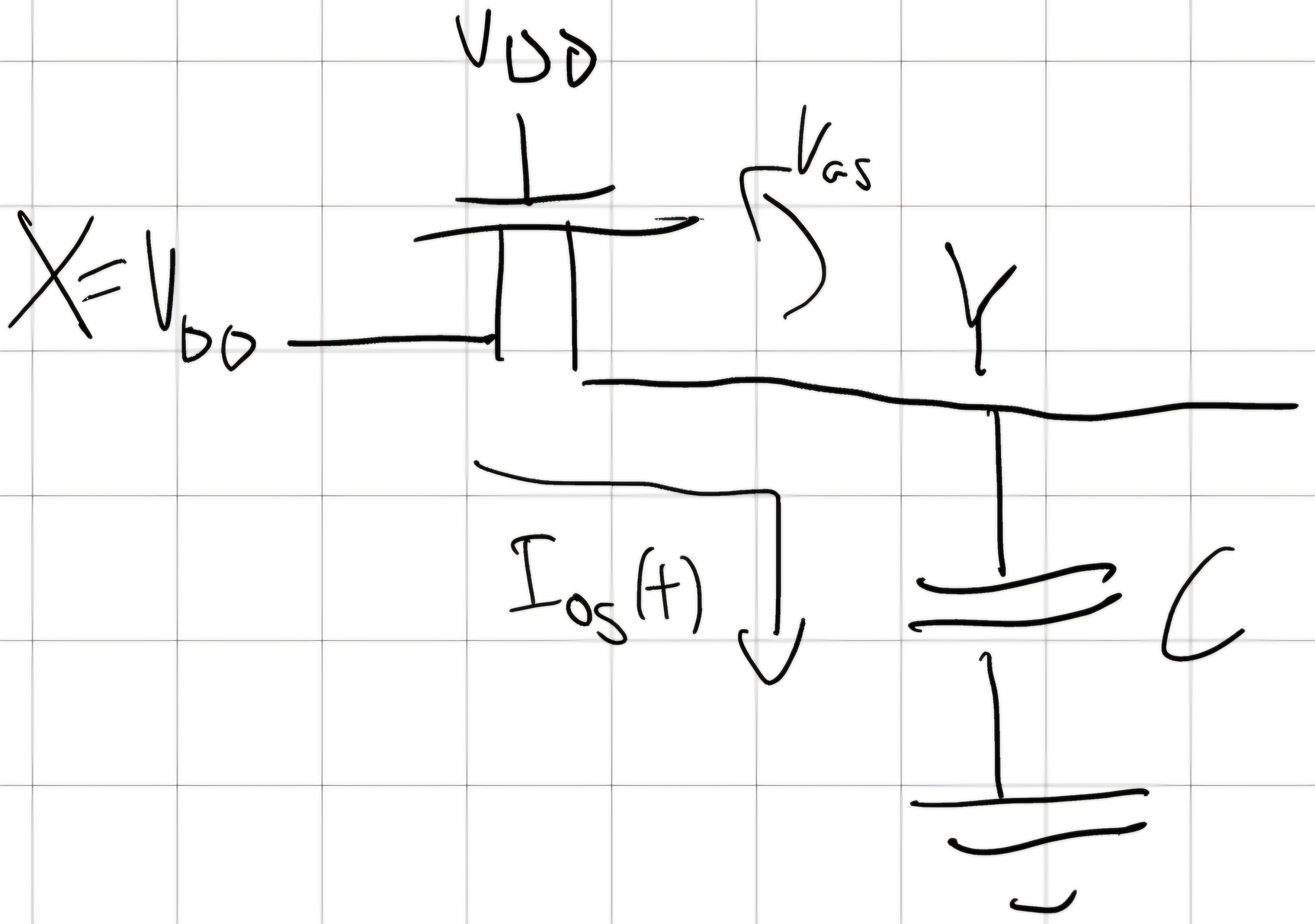
Source e Drain si comportano come vogliono, a seconda di come scorre la corrente cambiano posizione.
V_{GS} = V_{DD} - Y(t) si riduce fino a V_{GS} = V_{Th}, NMOS si spegne e smette di caricarsi, sempre satura la carica.
i_c(t) = I_{DS}^{SAT} (t) \\ C \frac{dY(t)}{dt} = K_n (V_{GS} (t) - V_{Tn})^2 \\ C \frac{dY(t)}{dt} = K_n (V_{DD} - Y(t) - V_{Tn})^2 \\ \frac{K_n}{C}dt = \frac {d Y(t)}{(V_{DD} - Y(t) - V_{Tn})^2} \\ \int_{0}^{t_{p,LH}}dt = \frac{C}{K_n} \int_{Y_L}^{Y_H} \frac{dY}{(V_{DD} - V_{Tn} - Y)^2} = \frac{C}{K_n}[\frac{1}{V_{DD} - V_{Tn} - Y}]_{Y_L}^{Y_H}
Con tecnologia F-CMOS
Y_H - Y_L = \frac{V_{DD}}{2} - 0 \\ t_{p,LH} = \frac{C}{K_n}(\frac{1}{\frac{V_{DD}}{2} - V_T} - \frac{1}{V_{DD} - V_{Tn}}) = \frac{C}{K_n} \frac{\frac{V_{DD}}{2}}{K_n(\frac{V_{DD}}{2} - V_{Tn})(V_{DD} - V_{Tn})} > \frac{C}{K_n} \frac{\frac{V_{DD}}{2}}{(V_{DD} - V{Tn})^2}
PMOS
Carica L \to H
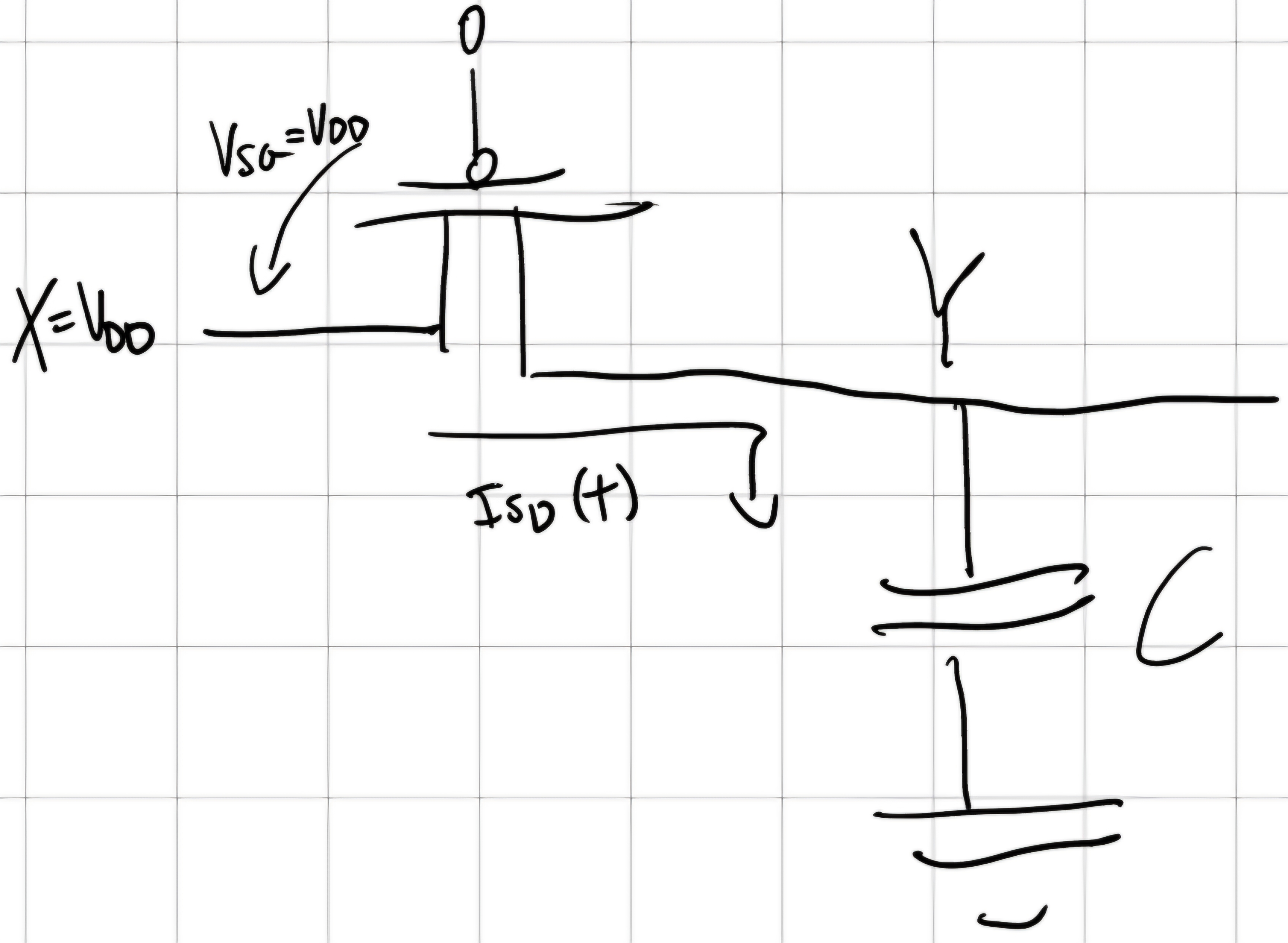
Fino a T = V_{DD} - |V_{ov}| siamo in satura, sa lì fino a V_{DD} in Ohmica, che noi trascuriamo.
I_{SD} (t) = -i_c(t) \\ I_{SD}(t) = -\frac{dY(t)}{dt} \\ t_{p,LH} = t_{p,LH}^{SAT} + t_{p,LH}^{OHM} \\ t_{p,LH} \cong \frac{C \varDelta Y}{K_p(V_{DD} - |V_{Tp}|)^2}
Scarica H \to L
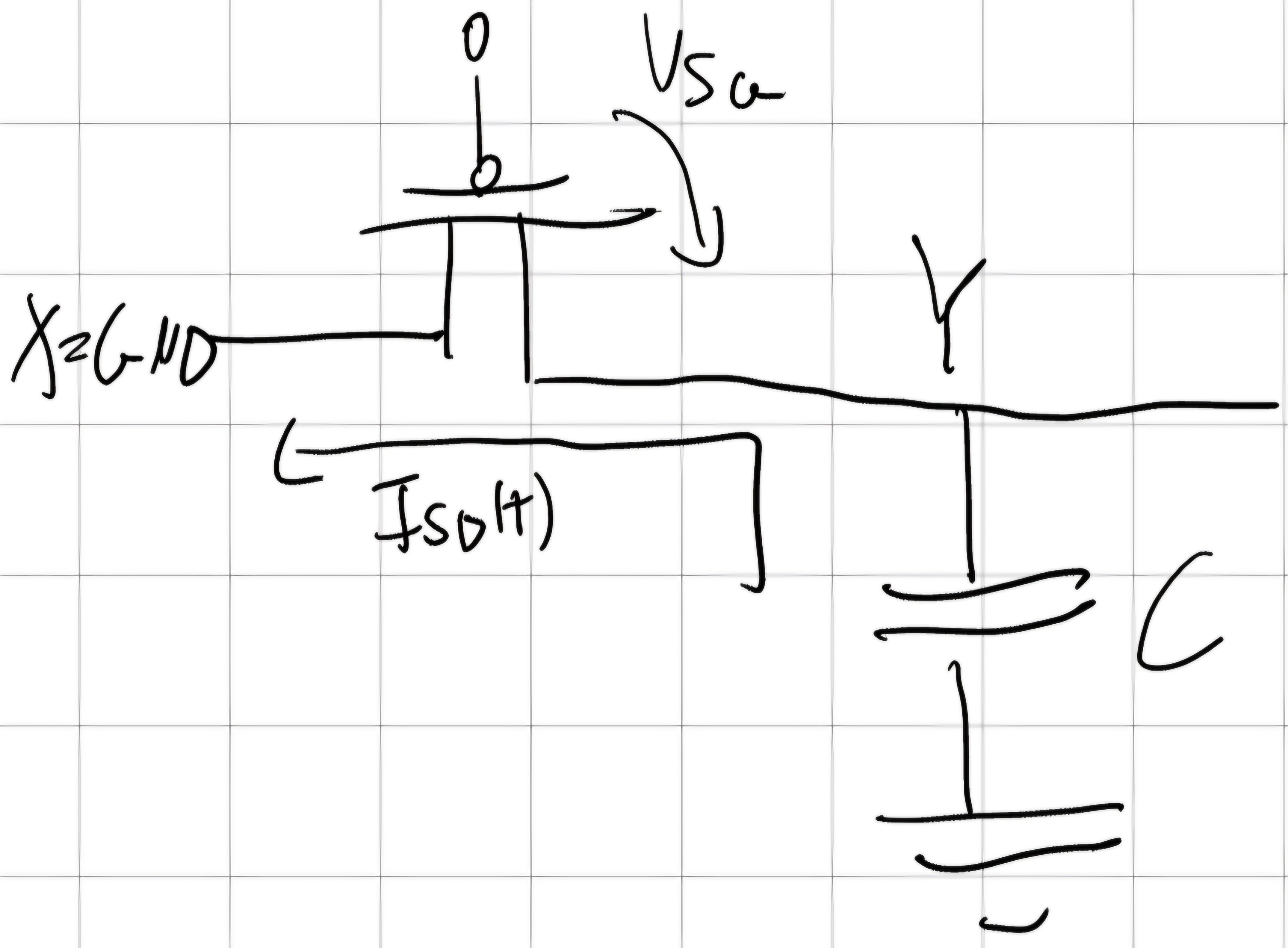
V_{SG} = Y(t) - 0 si riduce fino a V_{SG} = |V_{Tp}|, PMOS si spegne non si scarica più \implies PMOS sempre saturo.
I_{SD}^{SAT} (t) = - i_c (t) \\ K_p(V_{SG}(t) - |V_{Tp}|)^2 = - C \frac{dY(t)}{dt} \\ K_p(Y(t) - |V_{Tp}|)^2 = - C \frac{dY(t)}{dt} \\ -\frac{K_p}{C}dt = \frac{dY(t)}{(Y(t) - |V_{Tp}|)^2} \\ \int_{0}^{t_{p,HL}}dt = - \frac{C}{K_p} \int_{Y_H}^{Y_L} \frac{dY}{(Y(t) - |V_{Tp}|)^2} \\ t_{p,HL} = \frac{C}{K_p}[\frac{1}{Y(t) - |V_{Tp}|}]_{Y_H}^{Y_L}
Da F-CMOS
Y_H - Y_L = V_{DD} - \frac{V_{DD}}{2} \\ = \frac{C}{K_p}\frac{\frac{V_{DD}}{2}}{(\frac{V_{DD}}{2} - V_{Tp})(V_{DD} - V_{Tp})} > \frac{C}{K_p}\frac{\frac{V_{DD}}{2}}{(V_{DD} - V_{Tp})^2}
6.4 Transmission Gate Logic (TGL)
Mettiamo in parallelo NMOS e PMOS \implies aumento capacità corrente:
- Più area usata.
- Per pilotarlo abbiamo bisogno del segnale negato.
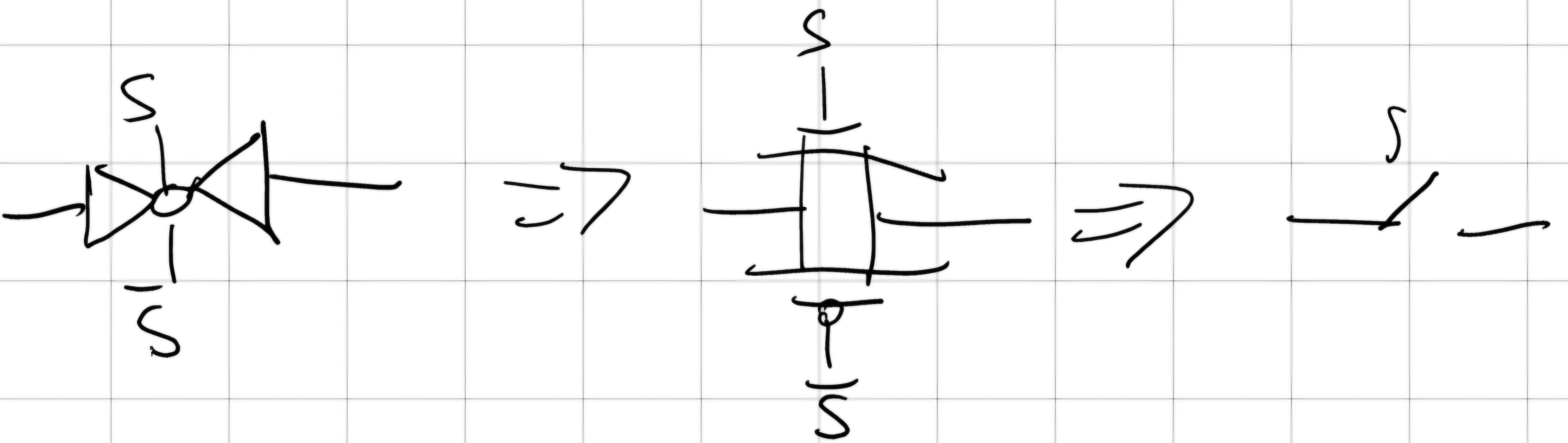
- Può essere un interrutore analogico.
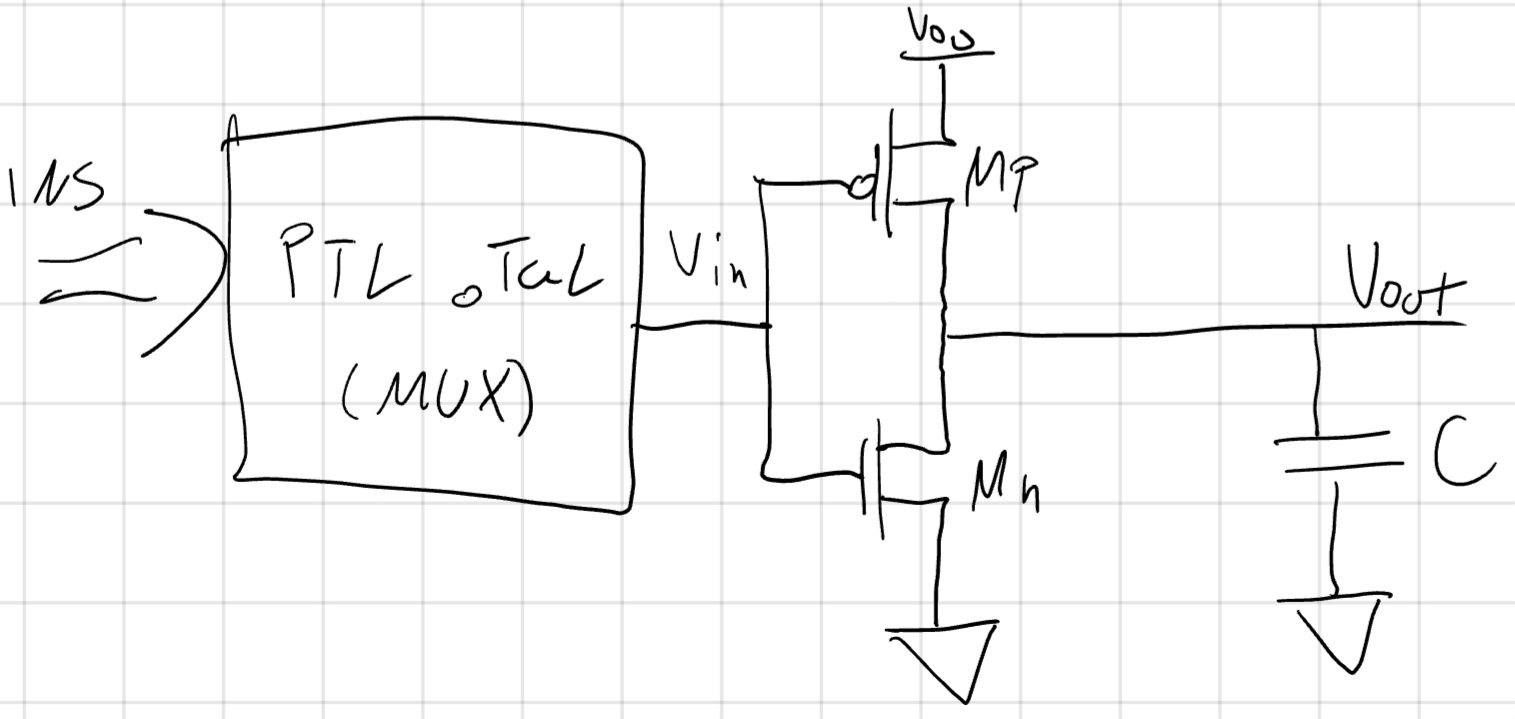
Complementary PTL
Lo colleghiamo a un F-CMOS così che F-CMOS si occupi:
- Rigenerare i livelli se necessario (PTL).
- Definire una soglia.
- Fa da driver do corrente, prende corrente dall’alimentatore.
Capitolo Sette: Circuiti sequenziali e memorie
Un circuito con memoria è un circuito che ha MEMORIA dello stato logico precedente, questi circuiti sono chiamati “bistabili”.
Esistono 2 tipi di bistabili:
- LATCH
- FLIP-FLOP
7.1 Bistabile
Il bistabile si può avere retroazionando i circuiti logici
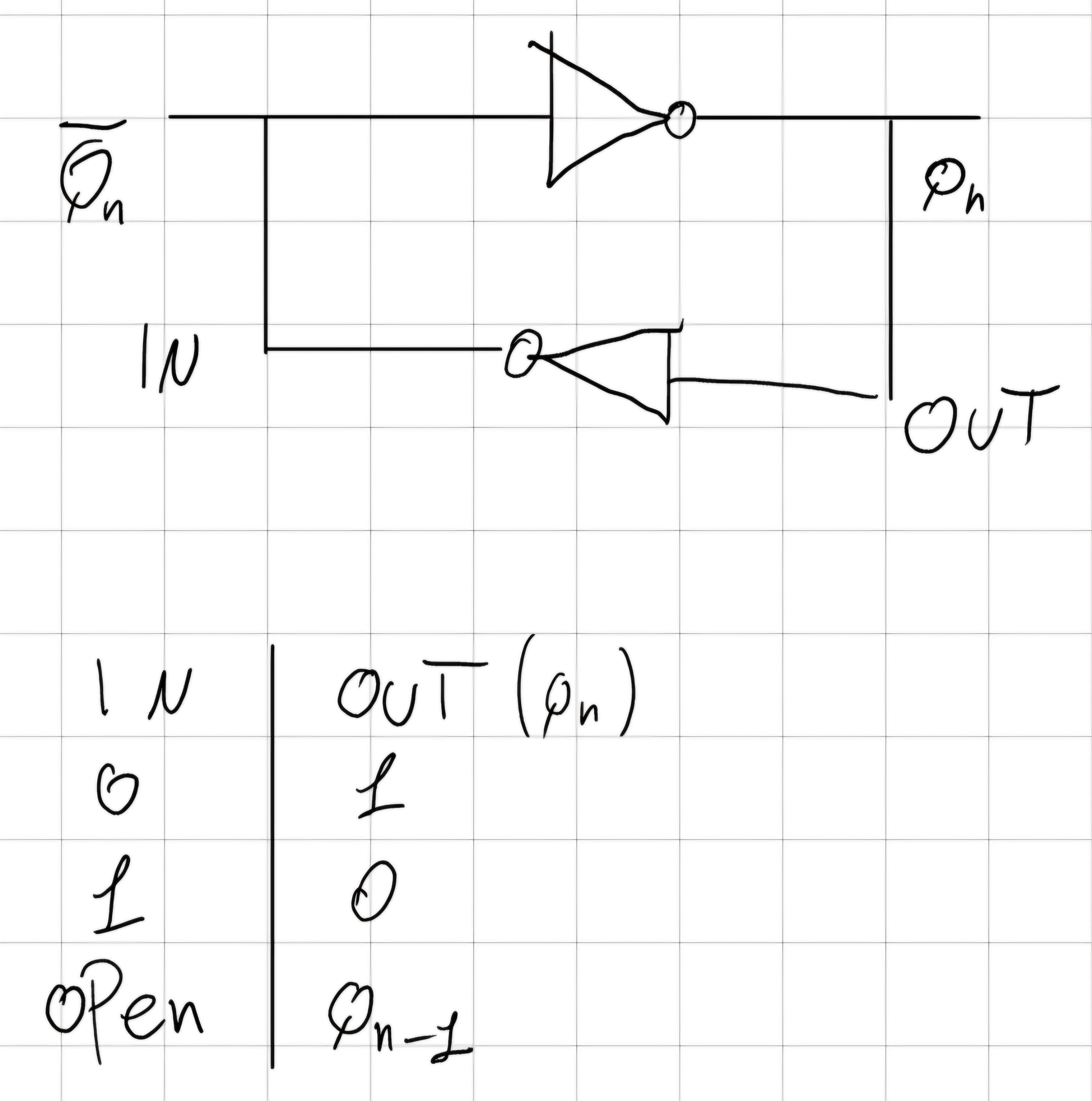
Se ora provassimo a disegnare su un grafico le caratteristiche della \color{orange}{NOT1} e \color{purple}{NOT2} notiamo che si hanno 3 punti di equilibrio, consideriamo inoltre la NOT2 come “curva di carico” della NOT1.
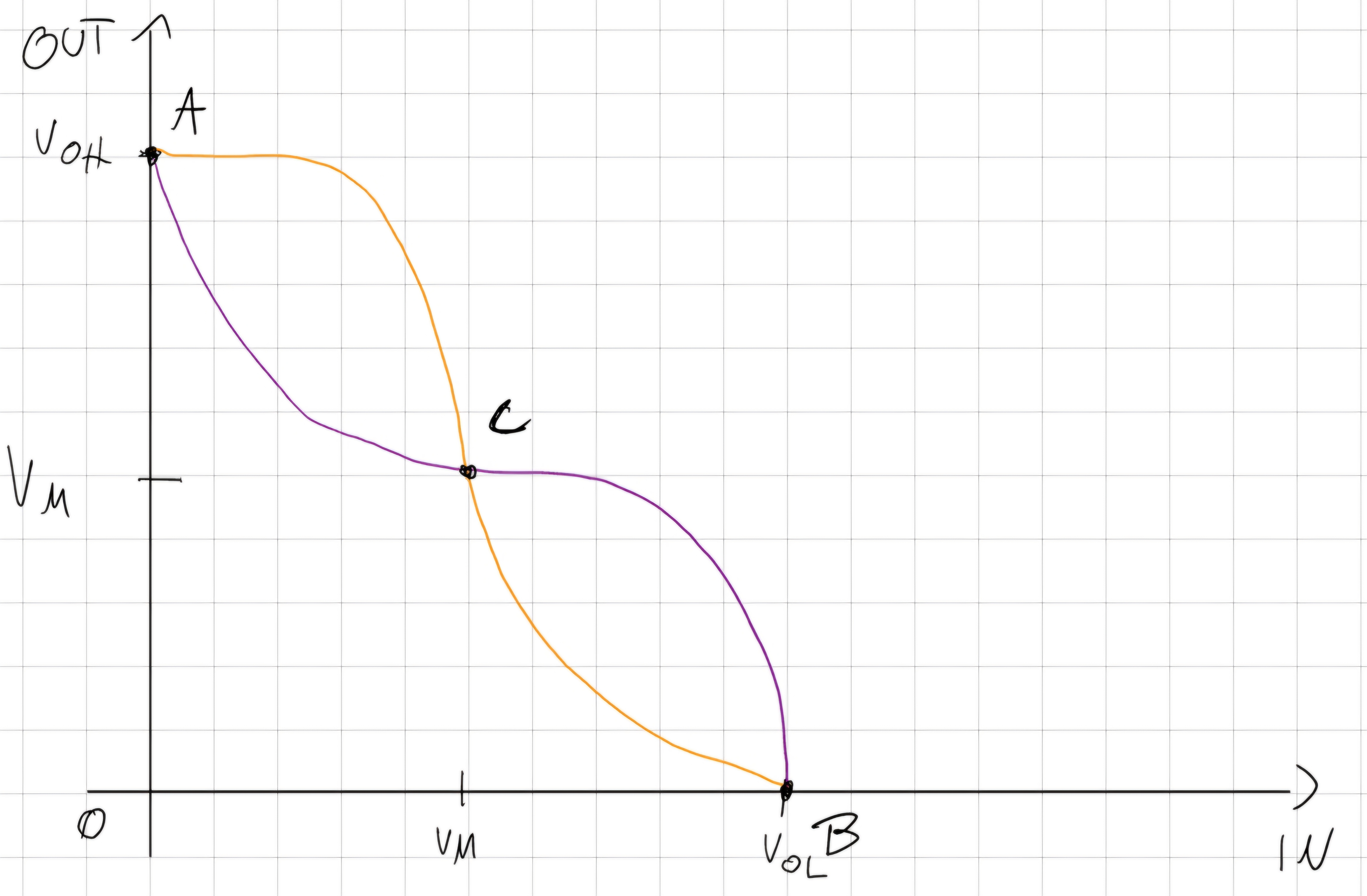
- A,1 logico, punto di equilibrio stabile, zona rigenerativa.
- B, 0 logico, punto di equilibrio stabile, zona rigenerativa.
- C, punto di equilibrio instabile, in zona lineare.
Ma come forziamo lo stato ?
Un esempio è trasformare le NOT in NOR con la GRN (R e S)
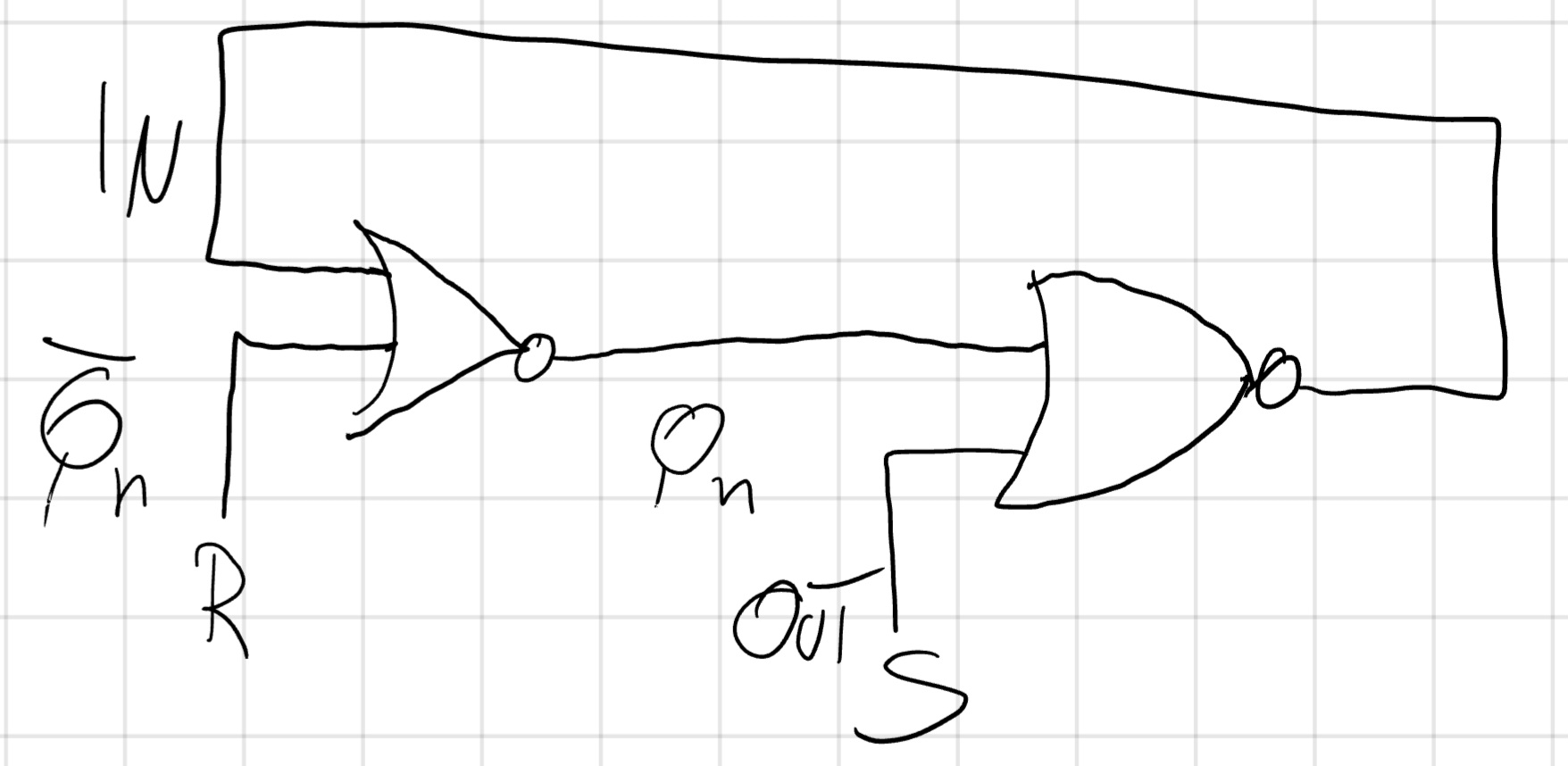
Se pilotiamo le GND possiamo forzare IN e OUT a 0/1
- S=1 \to Q=1, \neg Q=0
- R=0 \to Q=0, \neg Q=1
Questi bistabili vengono chiamati “bistebile, SR” (Set Reset).
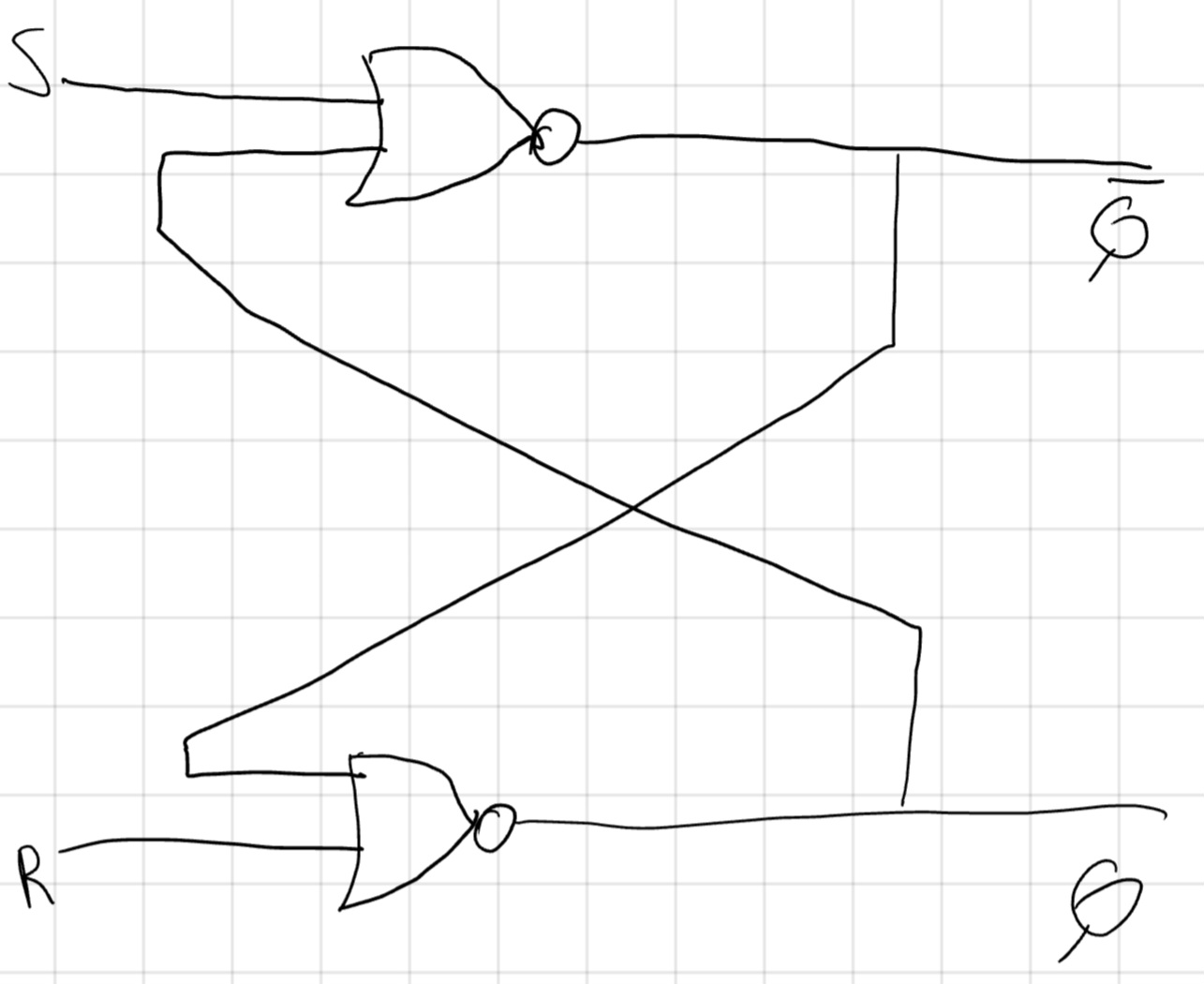
Mi rifiuto categoricamente di fare la tabella di verità della NOR perchè si conosce. Vediamo però quella del bistabile.
| SR | Q_n | \neg Q_n |
|---|---|---|
| 00 | Q_{n-1} | \neg Q_{n-1} |
| 01 | 0 | 1 |
| 10 | 1 | 0 |
| 11 | 0 | 0 |
N.B. lo stato “11” non viene usato.
Vediamo ora un “bistabile, \neg (SR)” con NAND al posto di NOR.
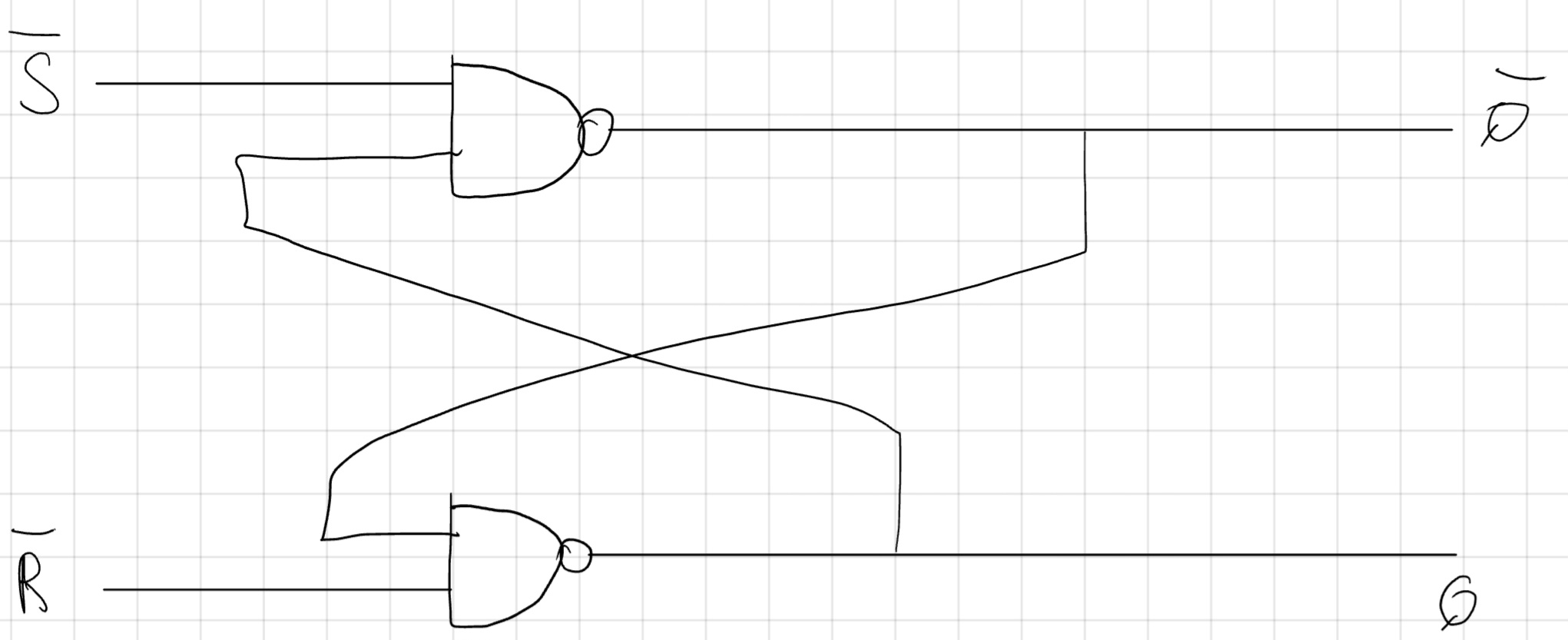
| \neg(SR) | Q_n | \neg Q_n |
|---|---|---|
| 00 | 1 | 1 |
| 01 | 1 | 0 |
| 10 | 0 | 1 |
| 11 | Q_{n-1} | \neg Q_{n-1} |
Ora vediamo un “Latch, SR” che è un bistabile con Enable.
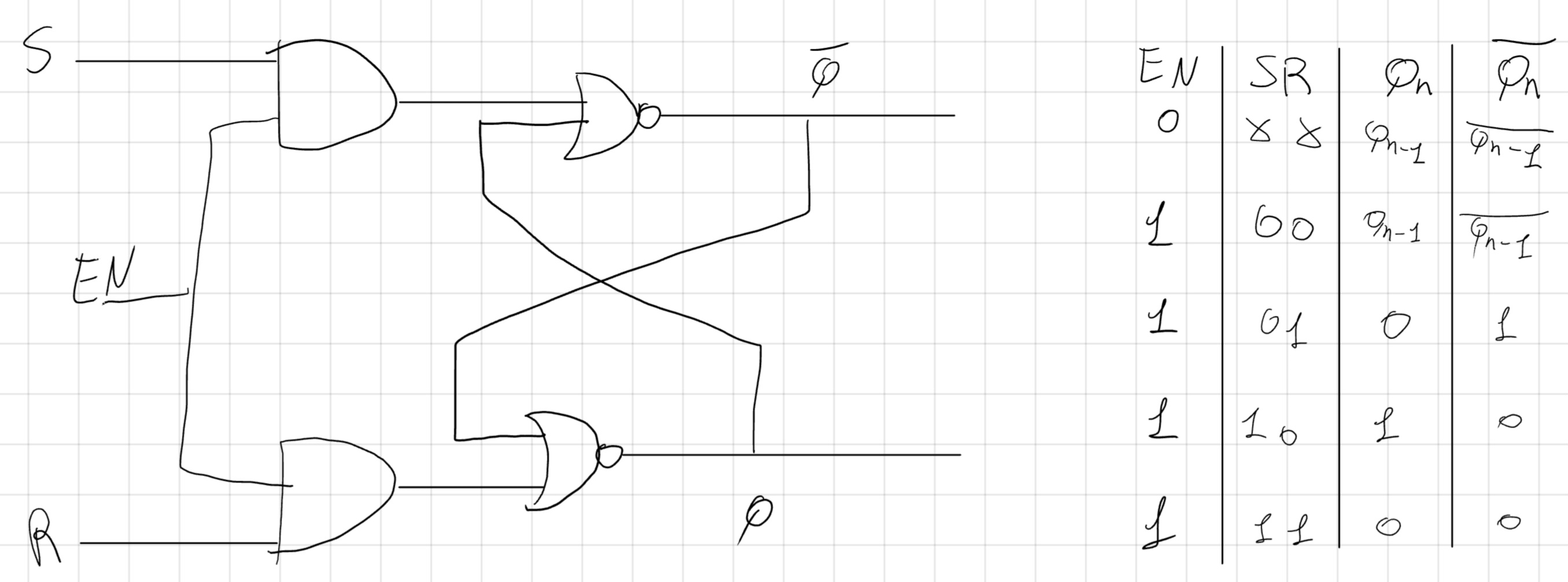
Si può sviluppare un bistabile che usa solo le configurazioni sensate.
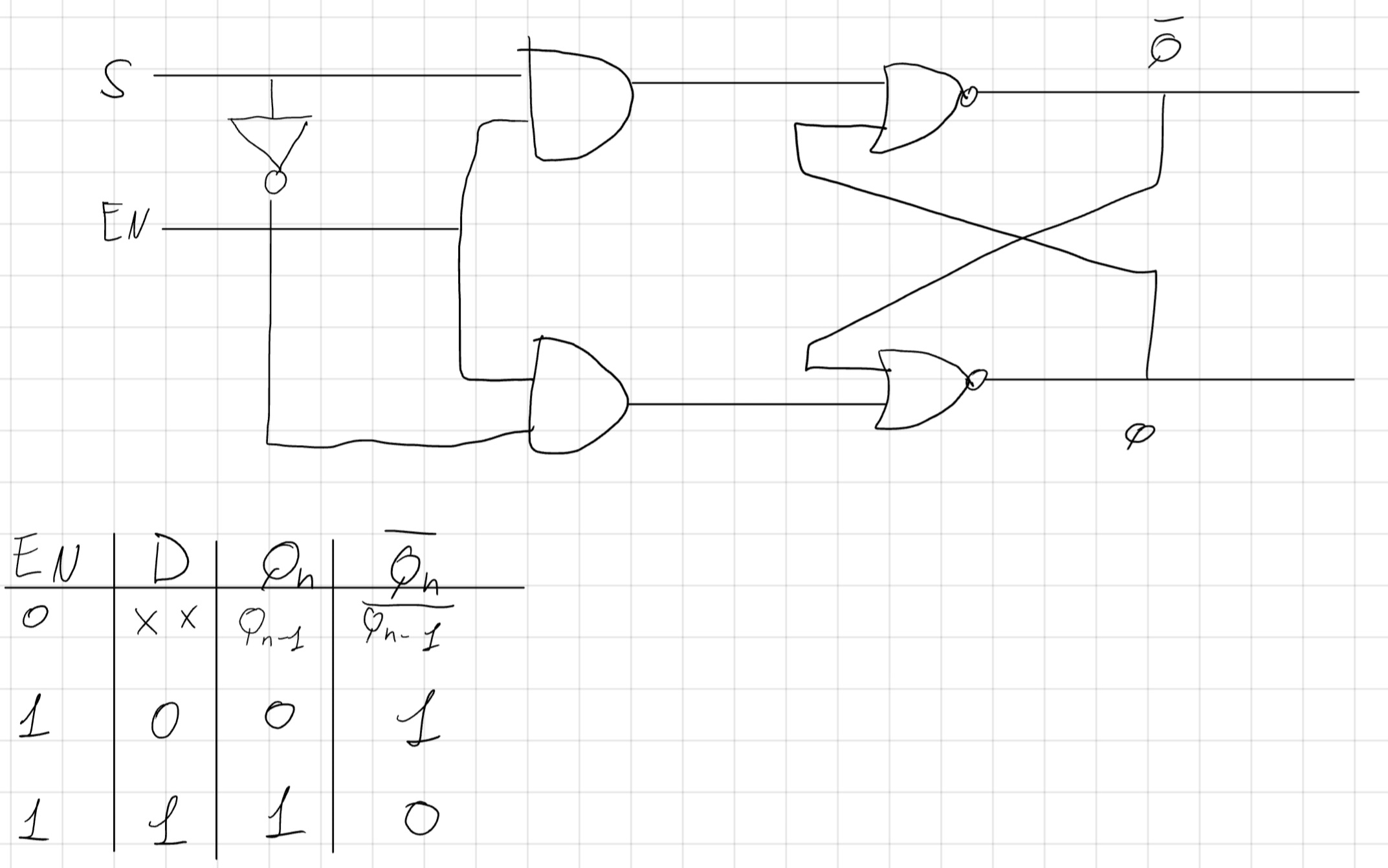
7.2 Flip-Flop
È semplicemente un bistabile con CLK (clock).
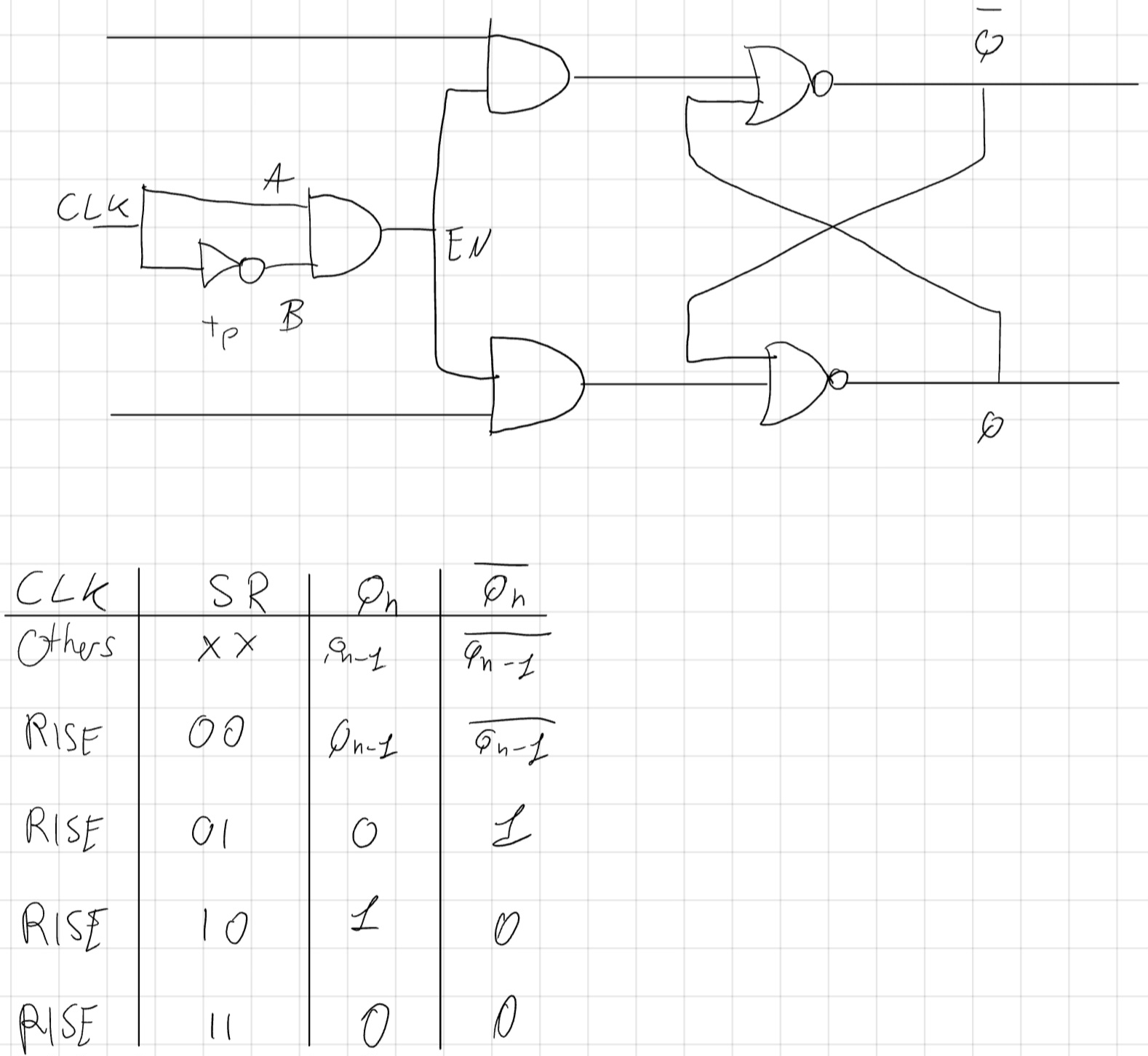
Vediamo il grrafico di cambio di livello logico di questo circuito.
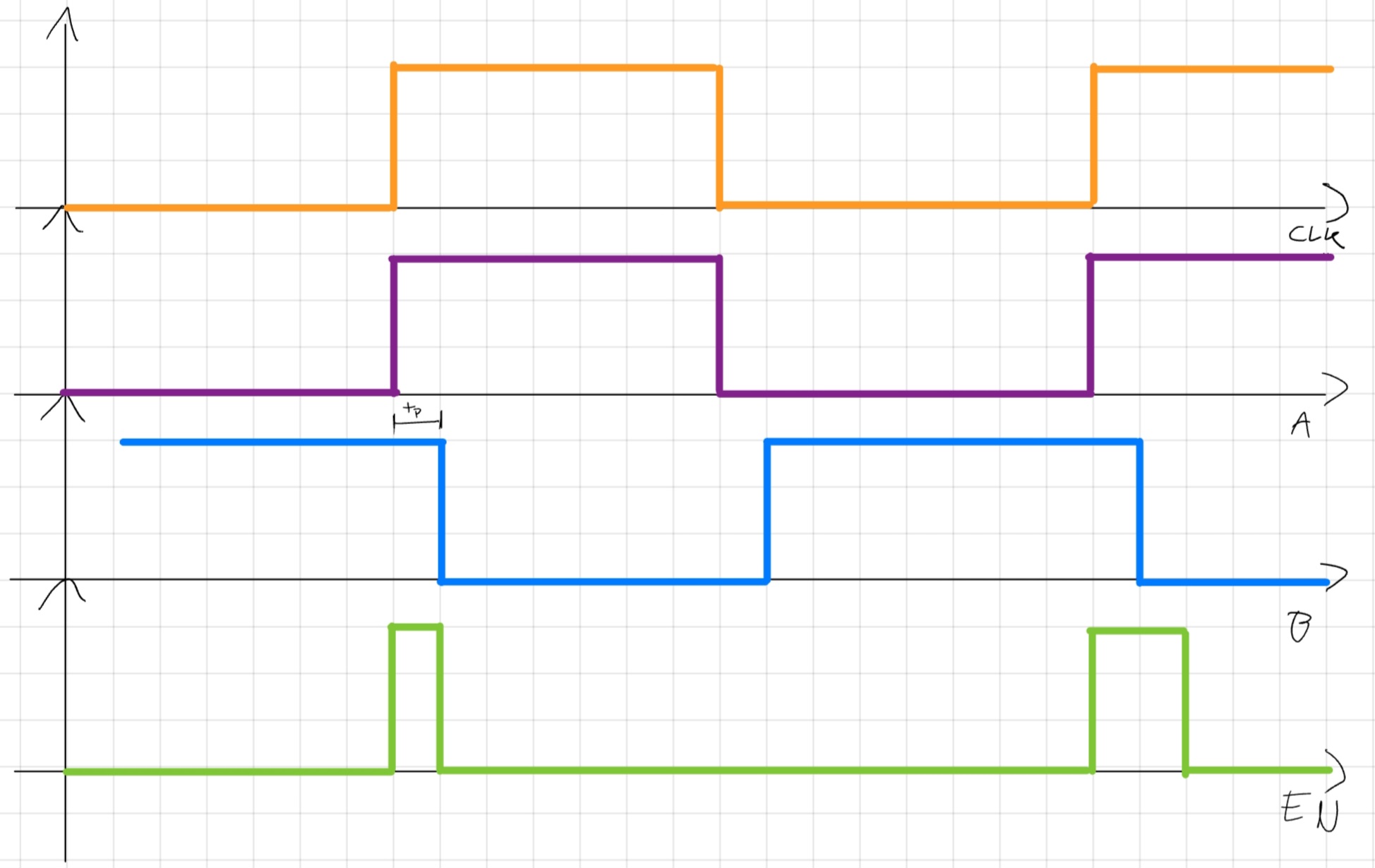
Qui torniamo ad AXO, anche questo presente su appunti ;), con il “Master-Slave”.
Edge Triggering
Possiamo essere sensibili in tanti modi:
Campionare ingressi e scriverli sul medesimo fronte.
- Fronte di salita (rising edge).
- Fronte di discesa (falling edge).
Campionare gli ingressi su un fronte (master) e scriverli sull’altro.
- Master Slave rise/fall.
- Master Slave fall/rise.
Insomma ci sono tanti richiami ad AXO, quindi andiamo a qualcosa di nuovo.
Vediamo una CMOS bistabile a NOT.
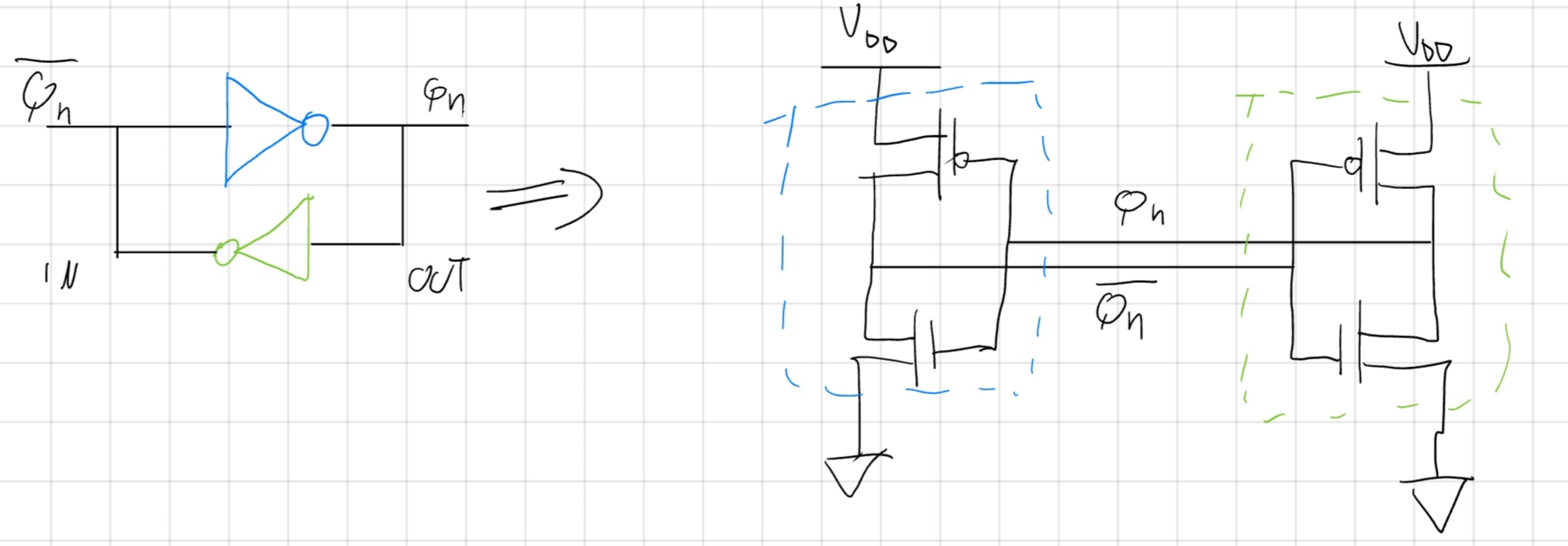
Timing
I tempi di carica/scarica dei MOS sulle capacità parassita creano vincoli di timing su latch e flip-flop.
- Tempo di Set-Up, tempo con cui un segnale d’ingresso deve rimanere stabile prima di passare in fase MEMO.
- Tempo di Hold, tempo per cui un segnale deve rimanere stabile anche dopo essere passati nella fase MEMO.
- Tempo di propagazione, MI RIFIUTO DI SPIEGARLO.
- Questi vincoli determinano la frequenza massima di funzionamento di un sistema digitale!
7.3 Pipeline
Le tecniche di pipeline servono per disaccopiare la relazione tra “Throughput” (T) e “Rate” (R).
Se consideriamo una logica combinatoria, il massimo rate è dato dall’inverso del massimo tempo di propagazione (D).
R= \frac{1}{D}
Se vogliamo memorizzare a ogni R lavoreremo a un T_{MAX}=R.
Se spezzassimo la logica in N blocchi con ritardo di propagazione massimo = d_i, possiamo registrare ogni uscita con un flip-flop.
Ogni blocco se considerato indipendente può sopportare un rate r.
r_i = \frac{1}{d_i}
Per evitare accavallamenti e trascurando i timing di flip-flop, clockiamo il sistema e:

Otteniamo quindi:
- R = f_{CLK} = min\{\frac{1}{d_i}\}.
- T = \frac{1}{D}.
- Deduciamo che abbiamo vantaggi se bilancimo d_i, il best sarebbe \frac{D}{N} \to R = \frac{N}{D}.
7.4 Memorie
Ad oggi le memorie sono matrici 2D, possono essere:
Volatili (RAM), se tolgo corrente perdo tutto.
- SRAM
- DRAM
Non volatili, se tolgo corrente non perdo nulla.
- ROM
- FLASH
SRAM
RAM Statica
- Ogni cella ha un bistabile (4 MOS) più 2 MOS di selettori.
- Cella più veloce e facile.
- Dobbiamo dimensionare i MOS per leggere e scrivere.
- I tempi di propagazione determinano i tempi di accesso.
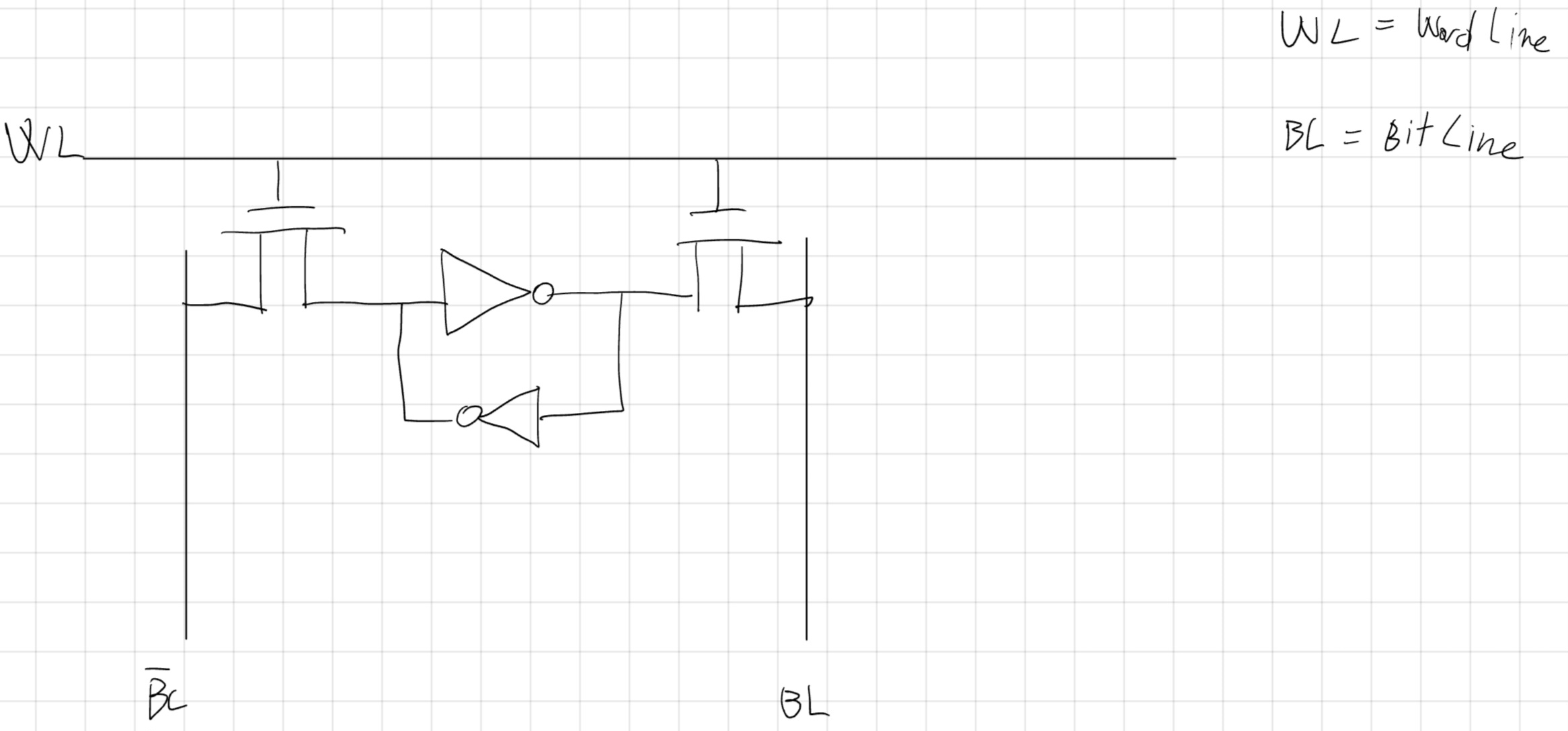
DRAM
- Ogni cella è composta da un condensatore (MOS parassita) e 1 MOS di selezione.
- Gestione complicata.
- La capacità si scarica in un lasso di tempo di qualche ms.
- I t_p determinano i tempi di accesso.
- In media più lenta di una SRAM.
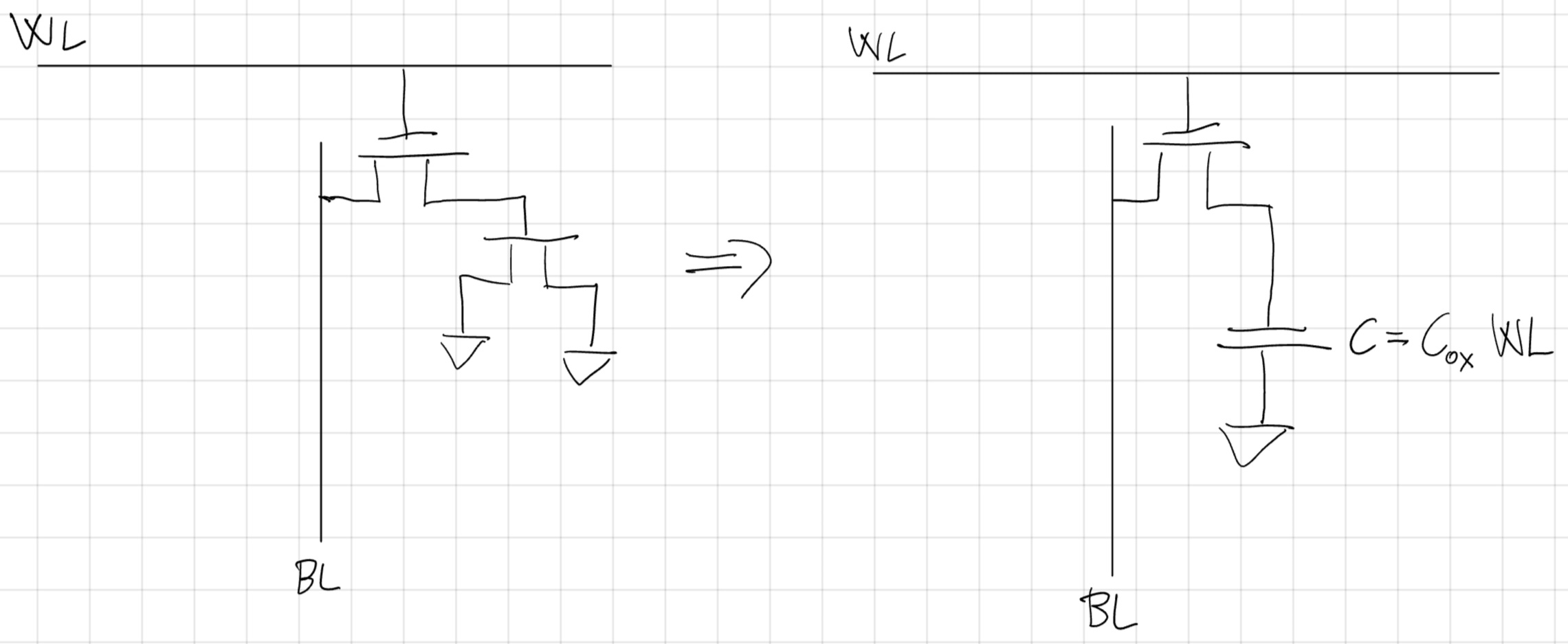
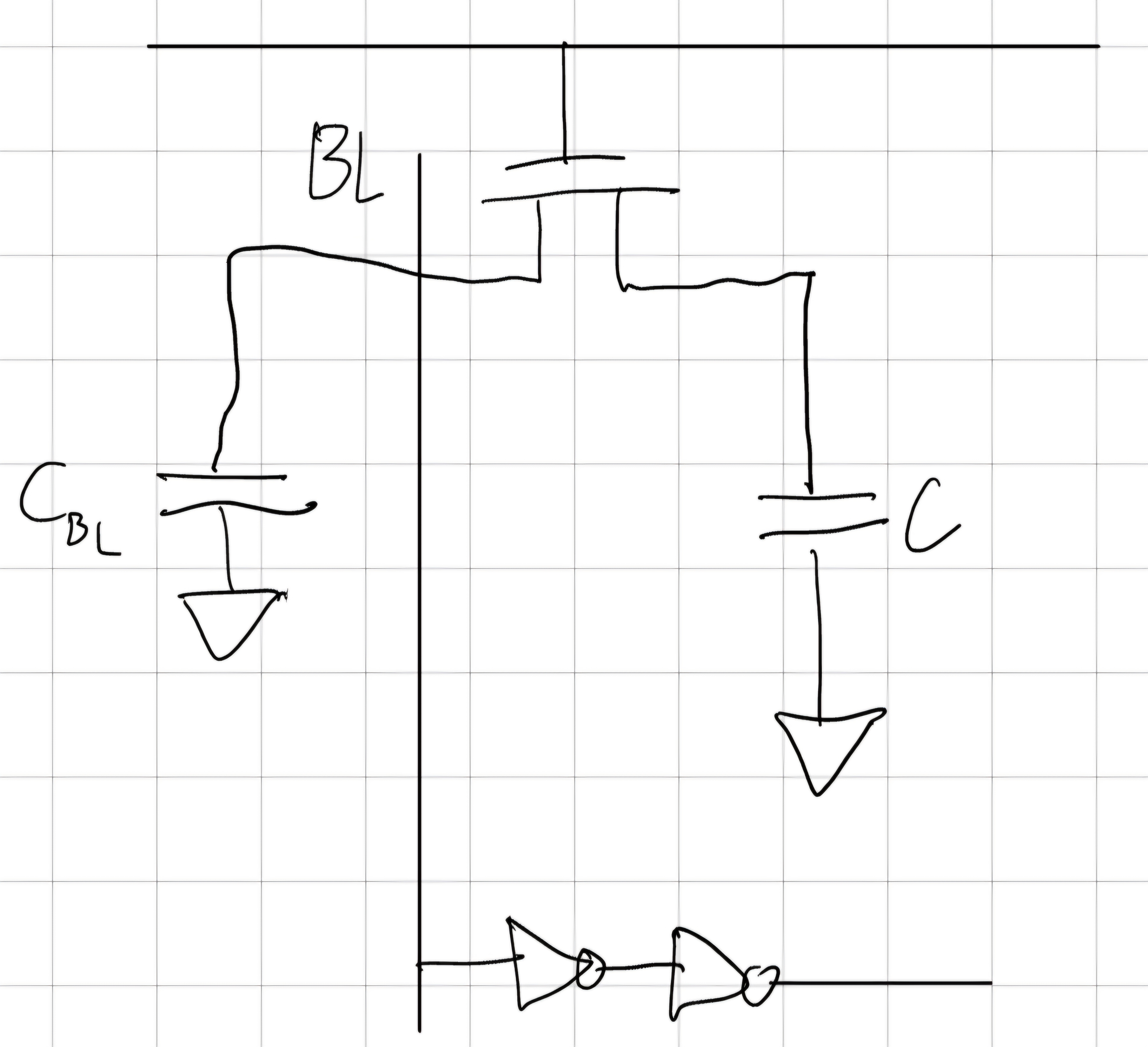
Scrittura DRAM
Uguale al PTL.
Scrivi ZERO (0V)
t_p=C \frac{\varDelta V}{I_{DS}^{SAT}}
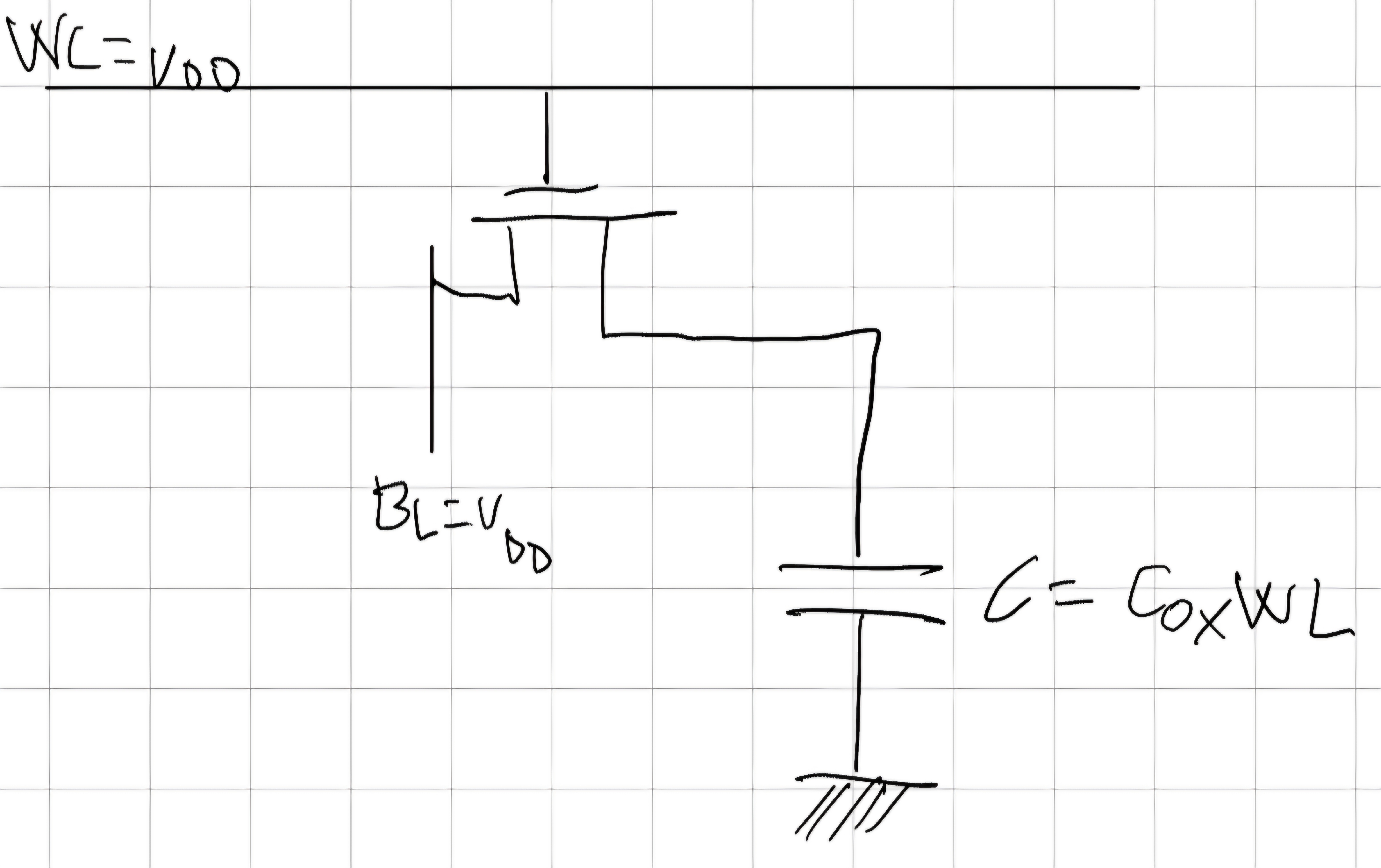
Scrivi UNO (V_{DD} - V_T)
t_{p,LH} = C \frac{\frac{V_{DD}}{2}}{K_n(\frac{V_{DD}}{2} - V_T)(V_{DD} - V_T)}

Lettura DRAM
In lettura consideriamo che la BL abbia una C_{BL} NON trascurabile.
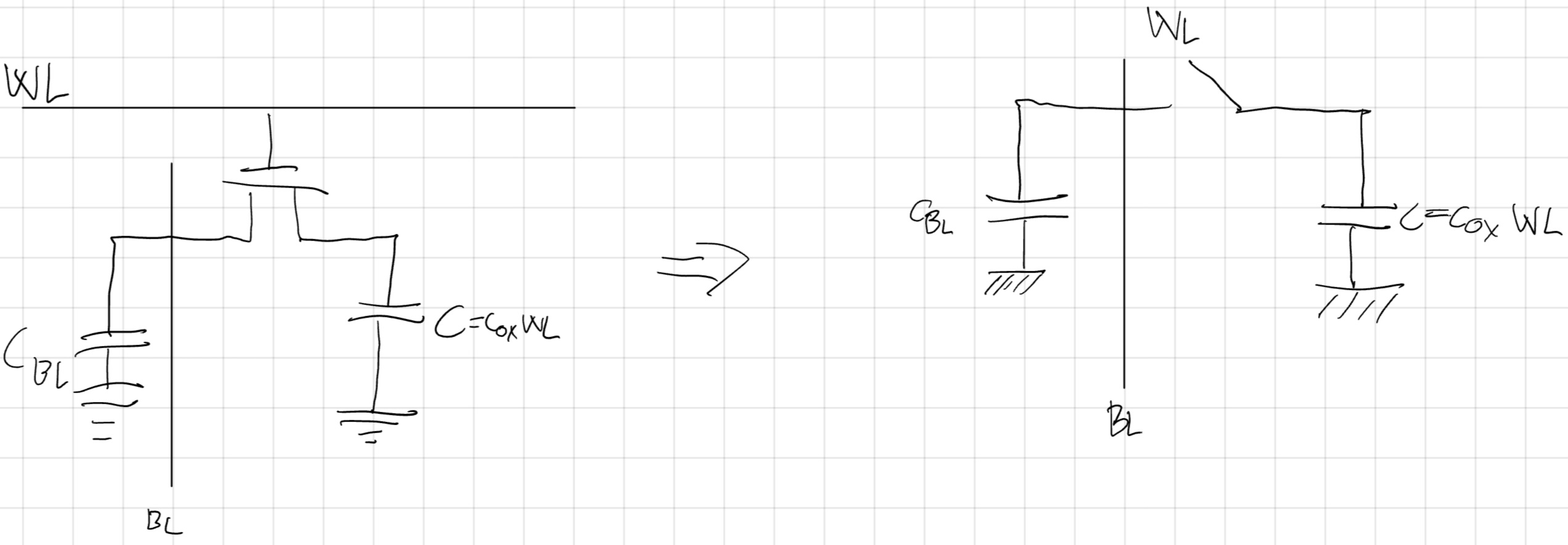
In questi casi possiamo avere il “charge sharing” tra le capacità che cambiano i livelli di tensione.
Esempio
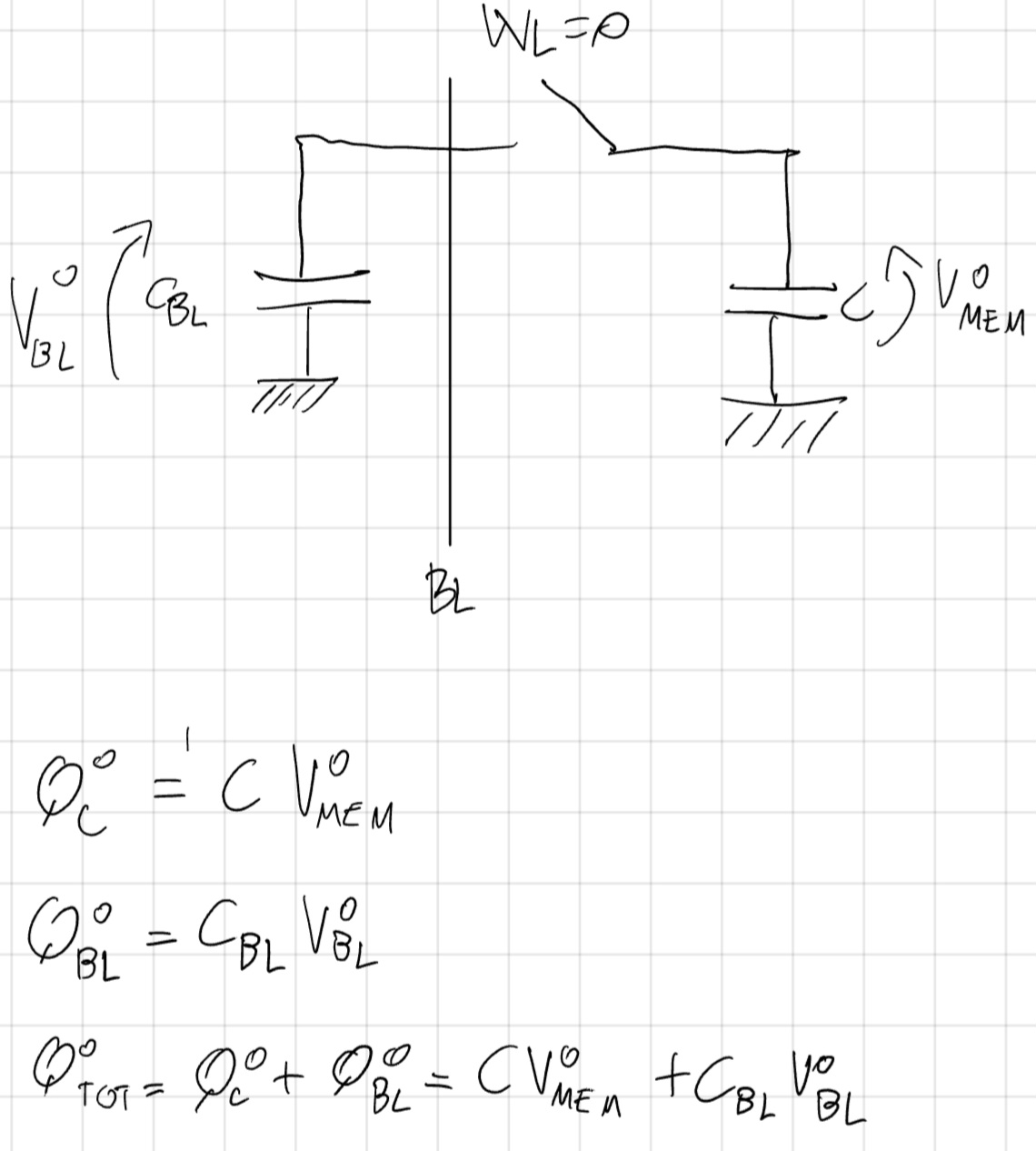
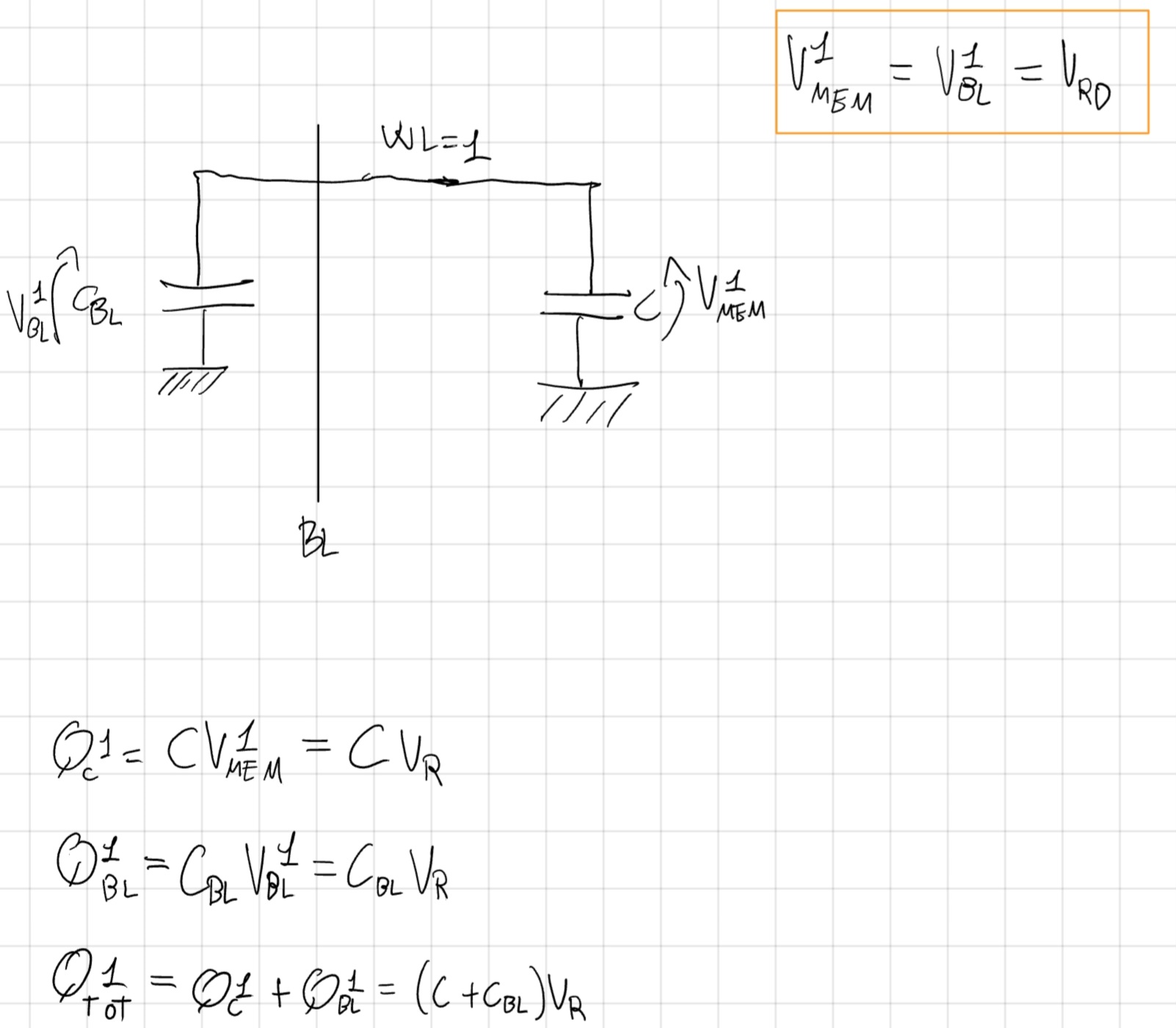
Se eguagliamo le cariche Q_{TOT}^1 = Q_{TOT}^0 otteniamo:
V_R = \frac{C V_{MEM}^0 + C_{BL}V_{BL}^0}{(C+C_{BL})}
- V_{BL}^0 = Tensione residua prima di effettuare la lettura, di solito la BL viene pre-caricata ad un V costante.
- V_{MEM}^0 = Tensione presente nella memoria a un valore compreso tra 0V e V_{DD}-V_T.
- V_R = Valore letto.
Dunque dobbiamo ripristinare i valori con un “buffer” che presenti una soglia adeguata ai livelli V_R.
Questo tipo di circuito si chiama “Sense Amplifier”.
ROM
Le ROM vengono realizzate connettendo Hard le celle a 0 o V_{DD}.
Esistono ROM programmabili (PROM) o One-Time-Programmable (OTP) dove la connesione a 1 o 0 viene effettuata rompendo dei fusibili.
FLASH
Le FLASH hanno una organizzazione simile alle DRAM.
- Il MOS parassita viene sostituito da un MOS floating-gate.
- Il MOS floating-gate, in funzione della differenza di potenziale tra WL e BL acquista una carica Q_F sul gate flottante.
- Si ha una V_T differente della solita.
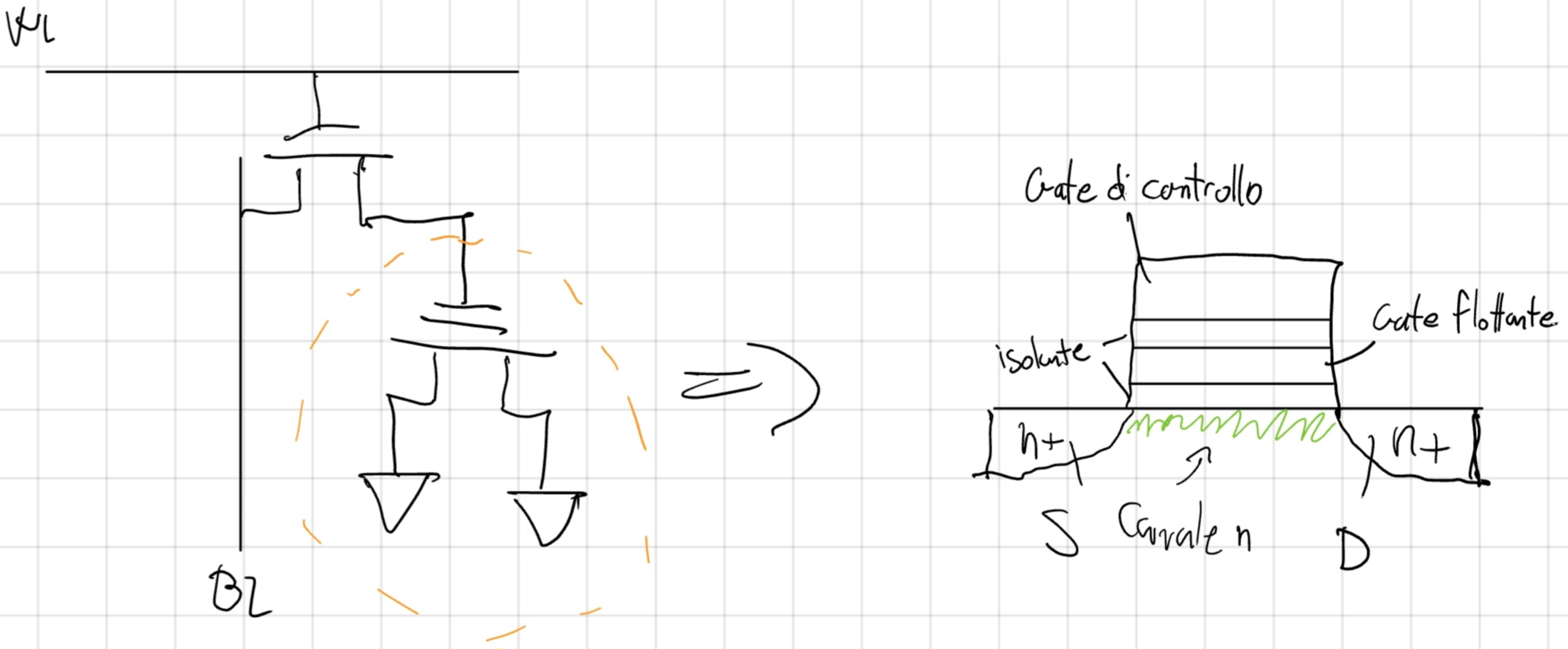
V_T = V_{T0} - \frac{Q_F}{C_{ox}}
Inoltre le FLASH sono 100-1000 volte più lente delle DRAM, questo perchè il floating-gate ha t_p molto grandi.
Memorie 3D
Si sta puntando a sviluppare memorie 3D.
7.5 Formule
Pipeline
Rate = R
t_p^{MAX} = D
R = \frac{1}{D}
Memorie
Capacità parassita MOS = C = C_{ox}WL
Scrittura DRAM (0) = t_{p,HL} = C \frac{\varDelta V}{I_{DS}^{SAT}}
Scrittura DRAM (1) = t_{p,LH} = C \frac{\frac{V_{DD}}{2}}{K_n(\frac{V_{DD}}{2}- V_T)(V_{DD}-V_T)}
Lettura DRAM = V_R = \frac{C V_{MEM}^0 + C_{BL}V_{BL}^0}{(C+C_{BL})}
FLASH
Nuova Soglia = V_T = V_{T0}- \frac{Q_F}{C_{ox}}
Capitolo Otto: Amplificatore Operazionale
Prima di iniziare un piccolo ricordo di cosa sono gli Amplificatori operazionali (o OpAmp).
Un amplificatori operazionale è un componente elettronico così ideato:
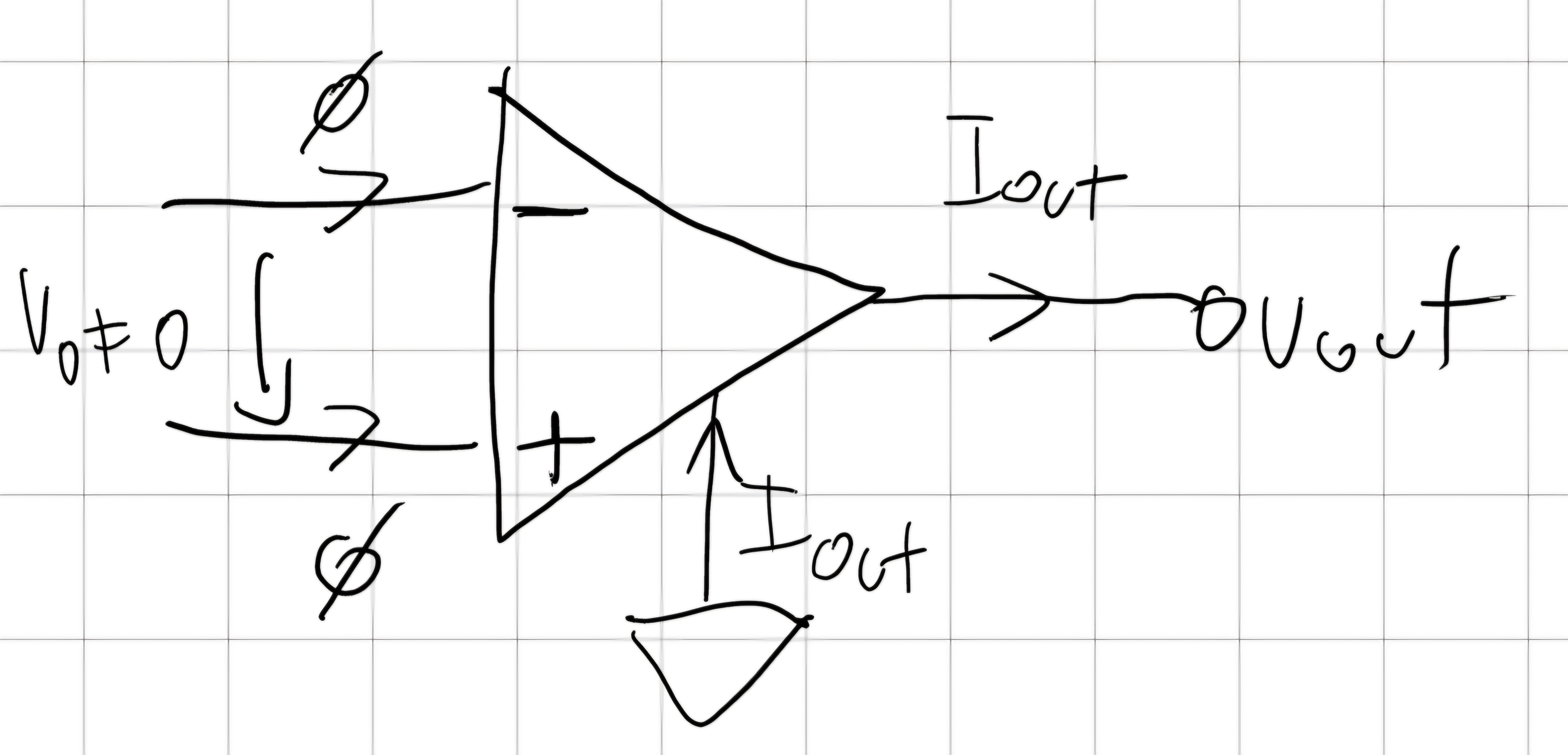
Quindi ingressi a corrente nulla e guadagno infinito questi amplificatori vengono definiti “ideali”.
8.1 Amplificatore operazionale Reale (l’inizio della fine)
Esistono 3 tipi di OpAmp reali o “Non Ideali”:
- Valutati in DC o polarizzazione.
- Valutati in AC o su segnale variabile.
- Valutati sia in AC che in DC.
N.B. Un generico segnale x(t), può essere visto come una costante x_{DC}(t) ed una variabile x_{AC}(t):
x(t) = x_{DC}(t) + x_{AC}(t)
Grazie ad F.D.A. lo studio di questo segnale ci tornerà più semplice.
8.2 Non idealità DC
Tensione di Offset
L’OpAmp a riposo mostra un uscita NON nulla.
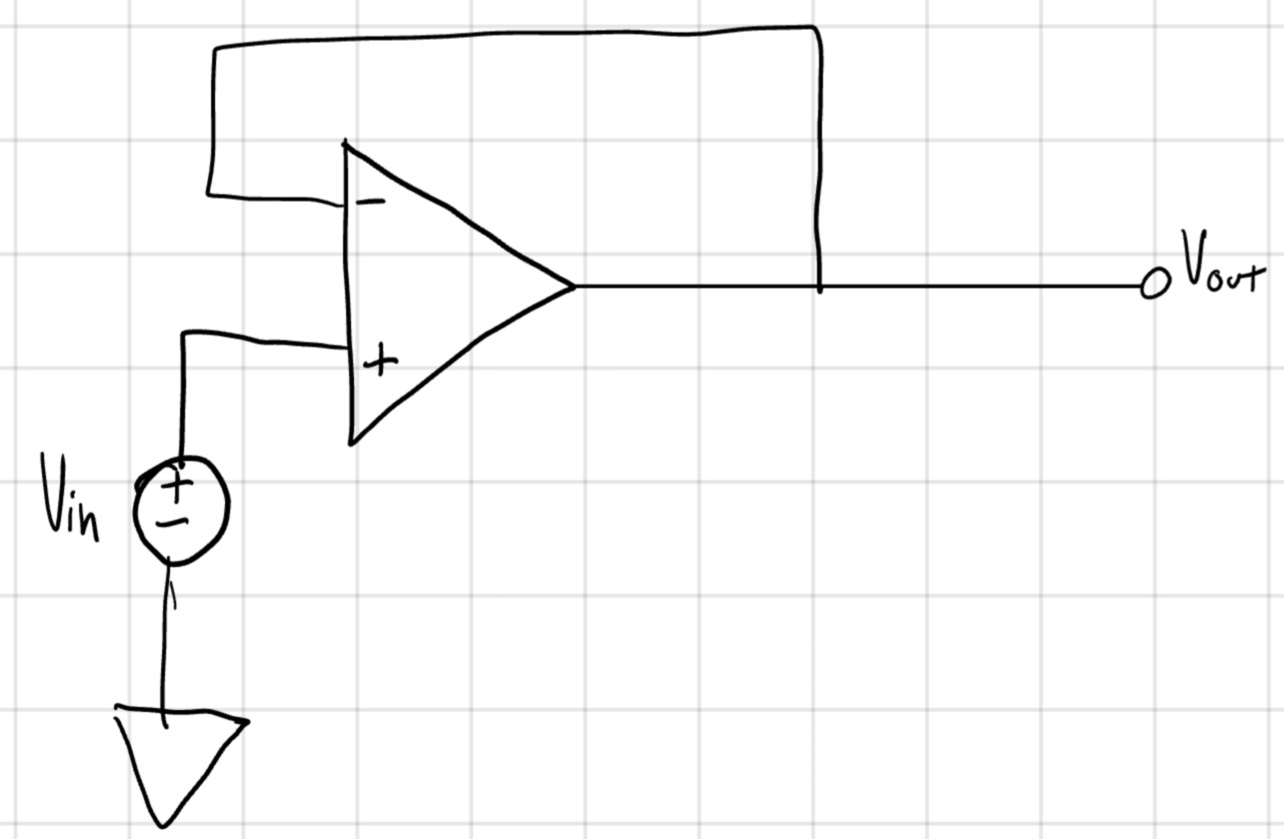
V_{out} = V_{in} + V_{OS}, if V_{in} = 0\implies V_{out} = V_{OS}
Ovvero anche se spenta V_{in}, l’OpAmp presenta una tensione V_{OS}, questo nel caso ideale NON accade, infatti nell’idealità V_{out} = V_{in}.
Si può usare il seguente modello ideale:
Corrente di Bias
Nel caso ideale la corrente entrante nell’OpAmp è zero, nel caso reale invece una corrente entrante è presente e viene chiamata “corrente di bias”.
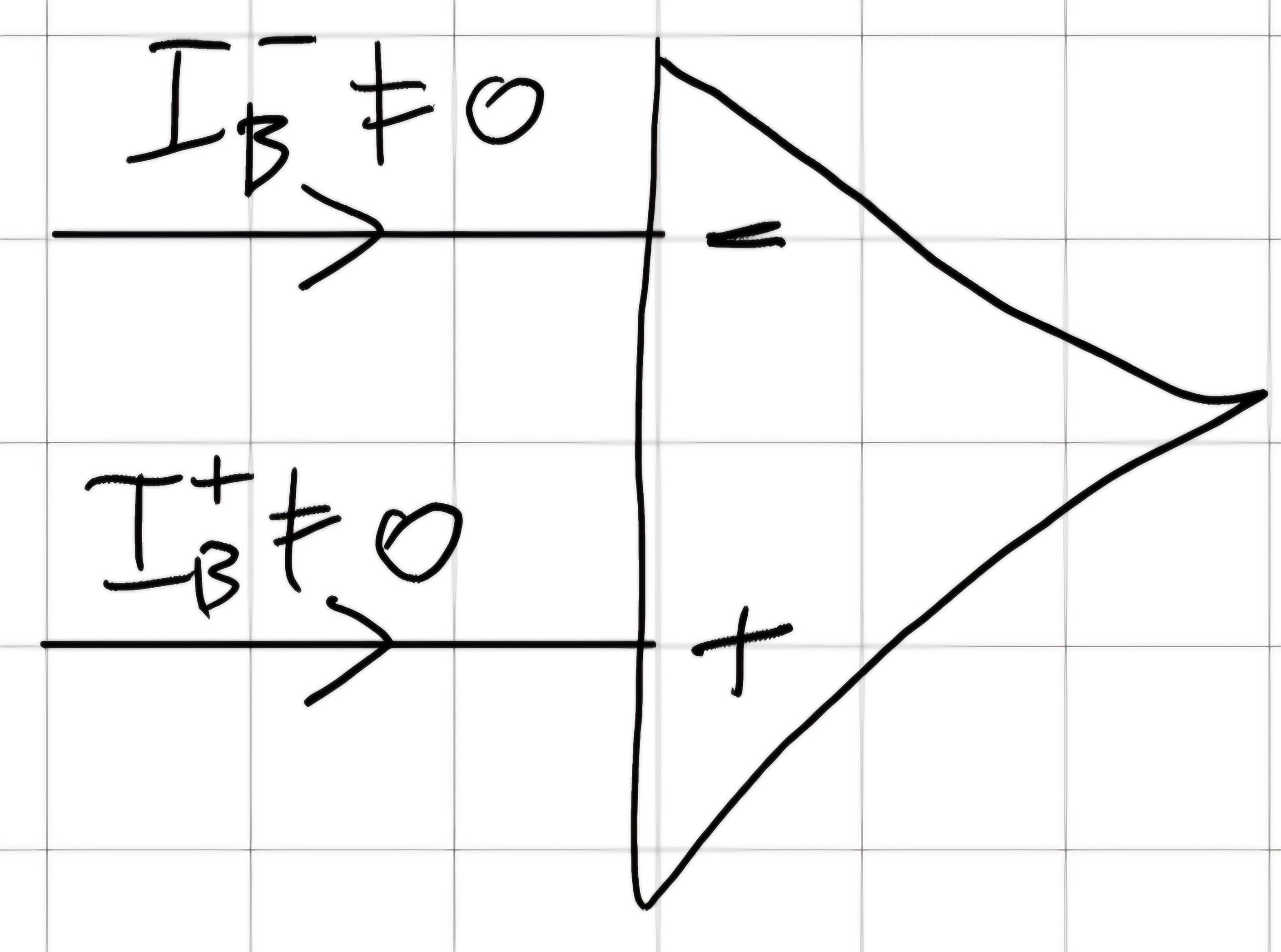
Per usare il modello ideale quindi:
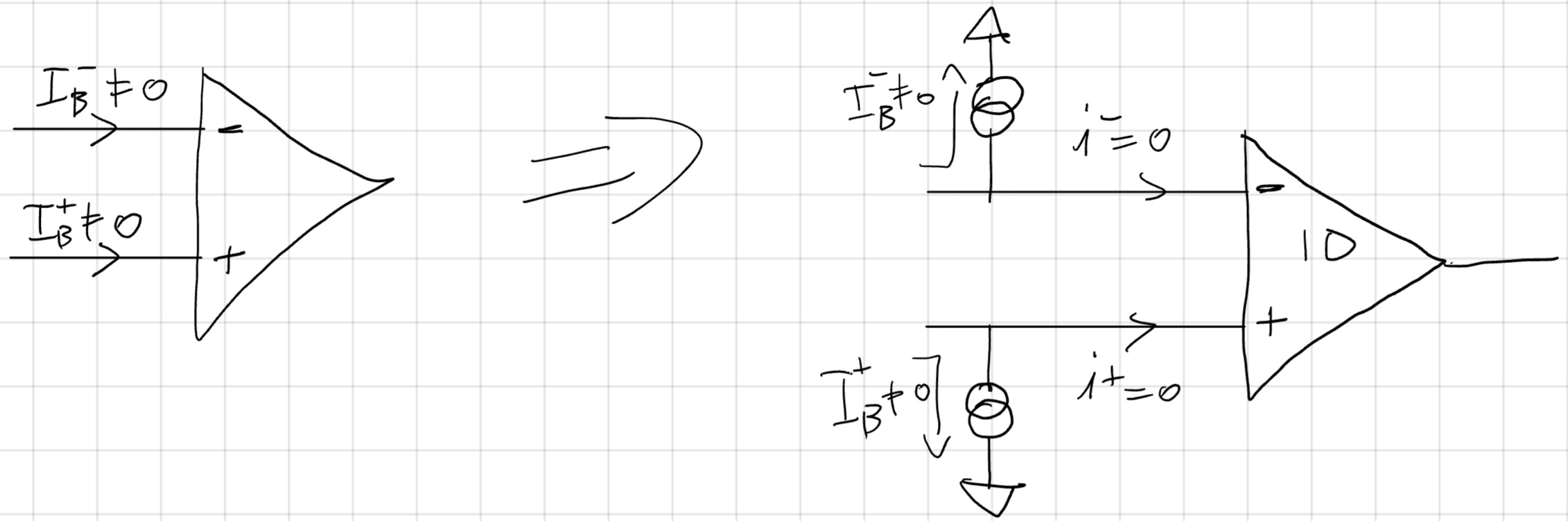
8.3 Non Idealità AC
Resistenza d’Ingresso
I fenomeni che generano la corrente di bias, si vedono come una resistenza all’ingresso:

Quindi usando il modello ideale:

Resistenza d’Uscita
L’OpAmp presenta una resistenza all’uscita per cui invece che registrare V_{in} = V_{out} registra |V_{out}| < |V_{in}|.
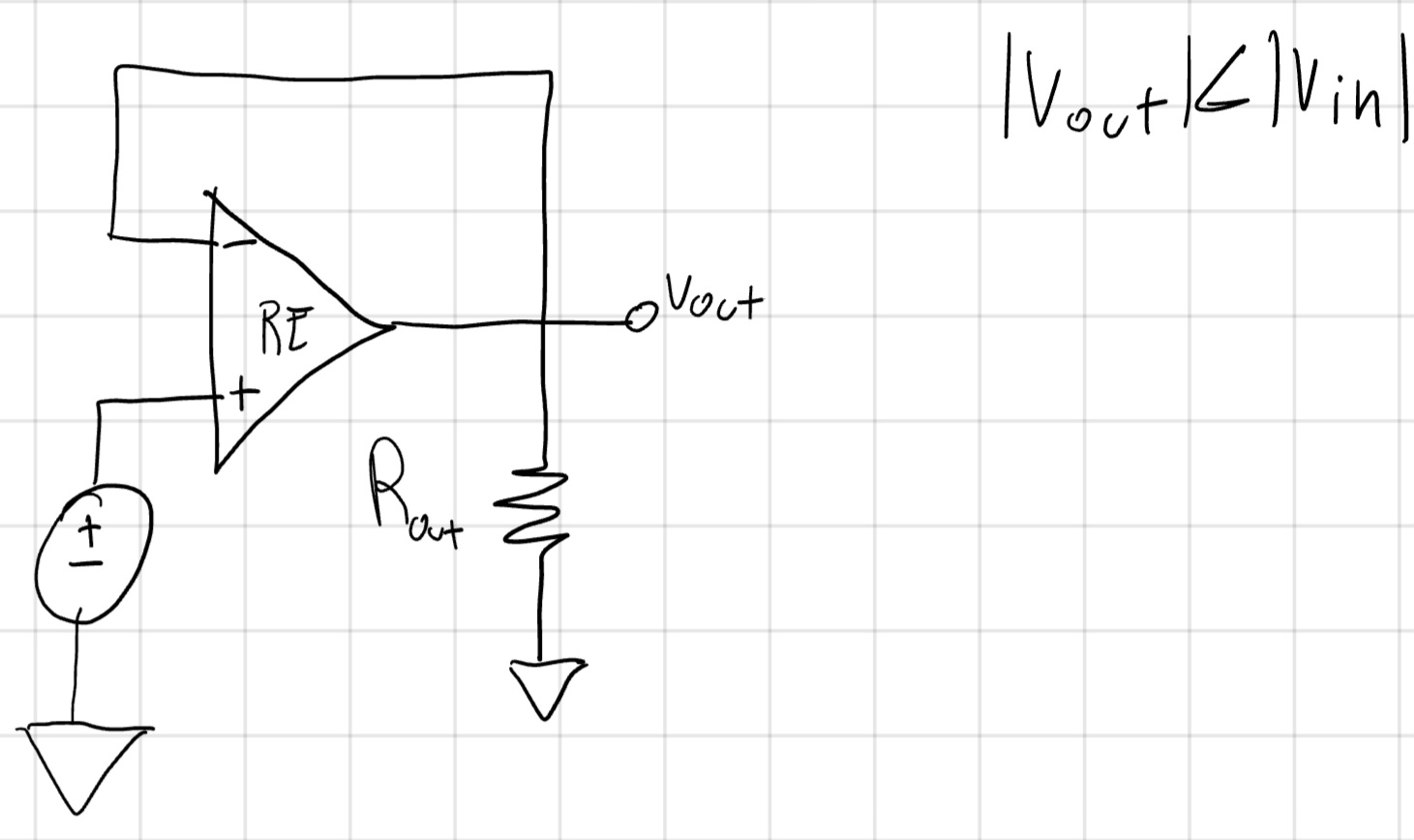
Per usare il modello ideale quindi:
Slew Rate
Questo effetto è maggiormente visibile in via grafica, si ha la pendenza massima all’uscita.
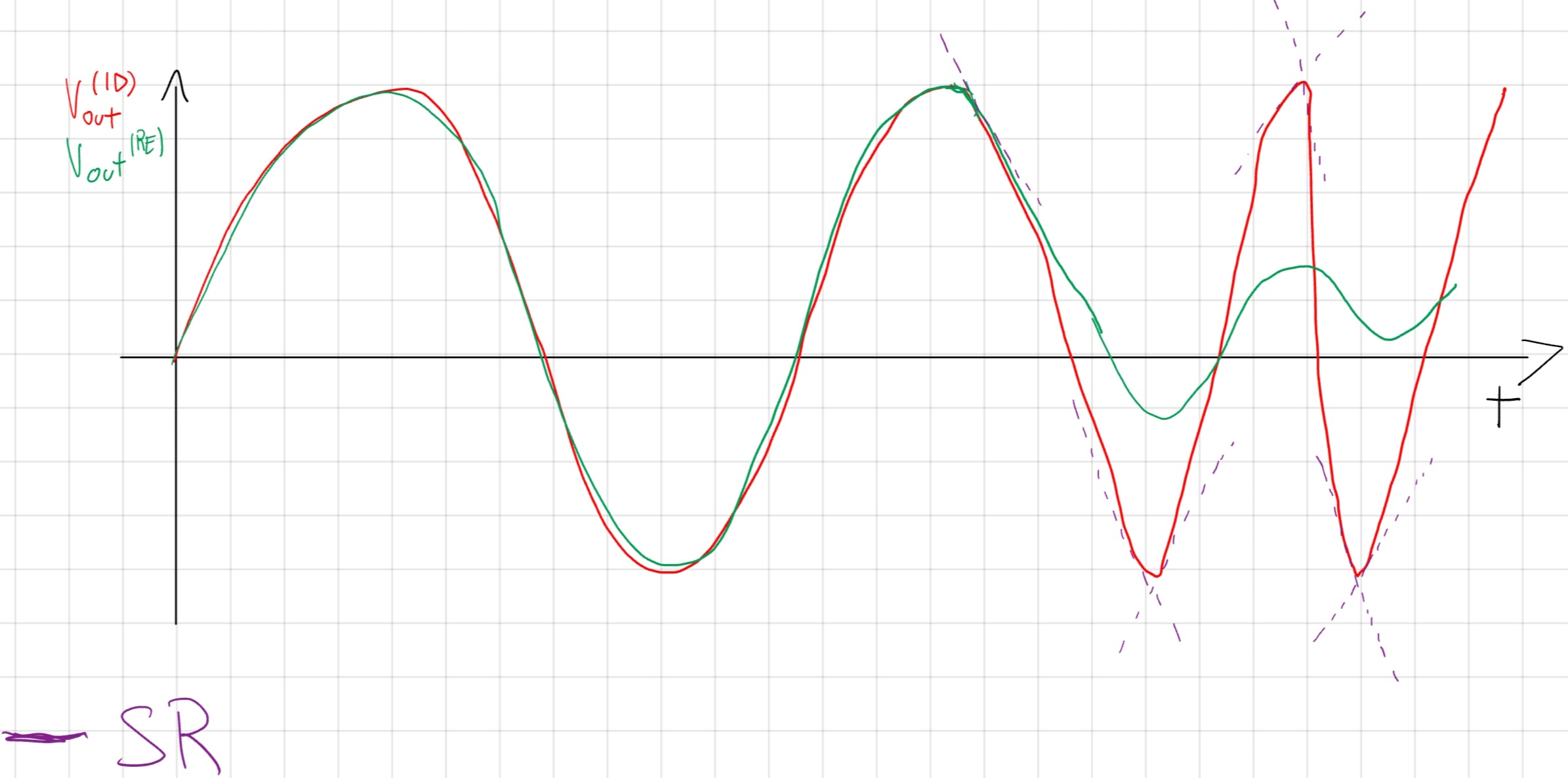
Esiste anche un quarto effetto che si chiama “Banda Limitata” che centra con le funzioni di trasferimento, quindi la guardiamo alla fine.
8.4 Non Idealità DC + AC
Massima tensione d’uscita
La tensione massima viene limitata a un V_{out}^{MAX}, anche se idealmente ci aspettiamo V_{out} = V_{in}.
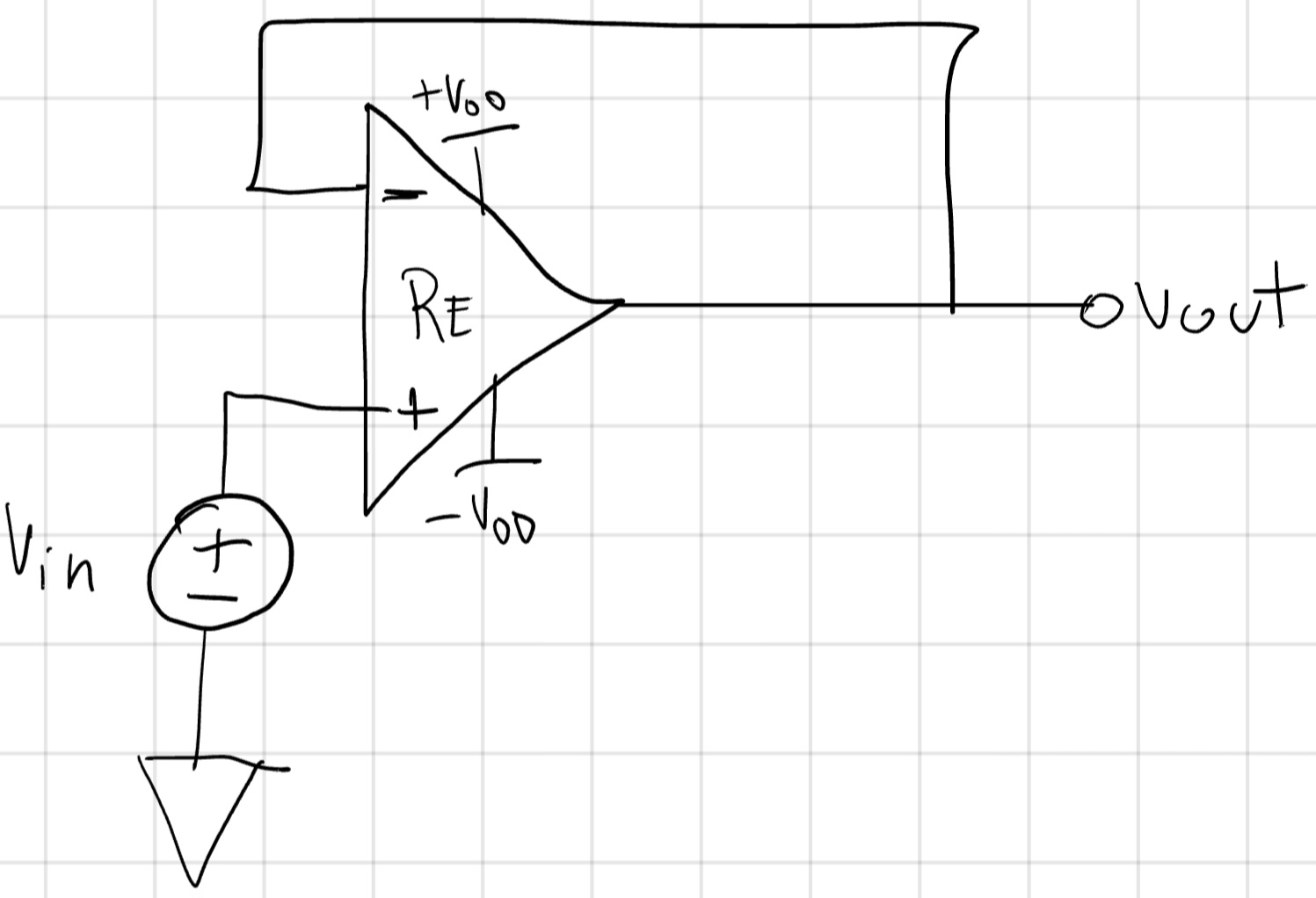
Di solito V_{out}^{MAX} \le V_{DD}, se uguale si chiama “op-amp rail-to-rail”.
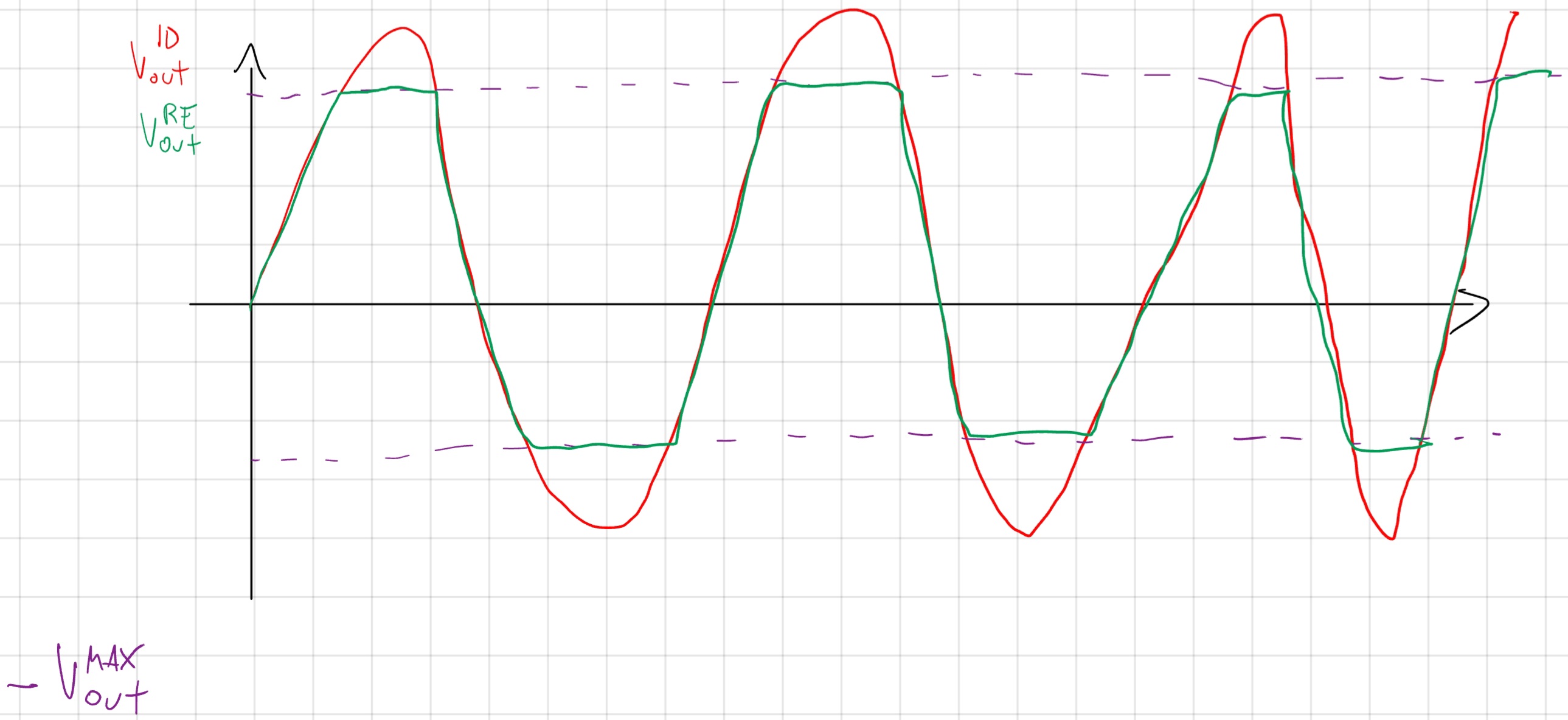
Massima corrente d’uscita
Stessa cosa ma con la corrente.
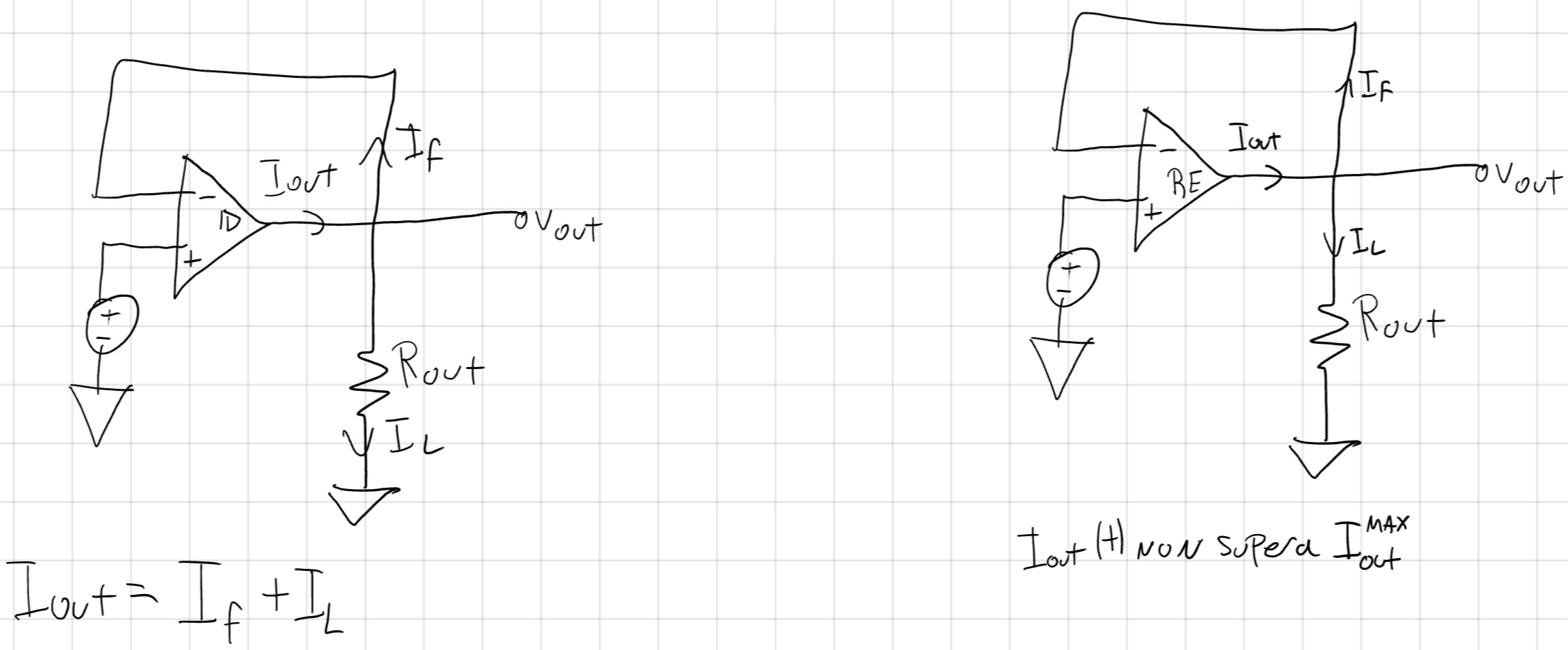
Solitamente I_f<<I_L, quindi I_{out} \cong I_L \implies V_{out} = I_{out}^{MAX} R_L.
Guadagno differenziale (open loop) finito
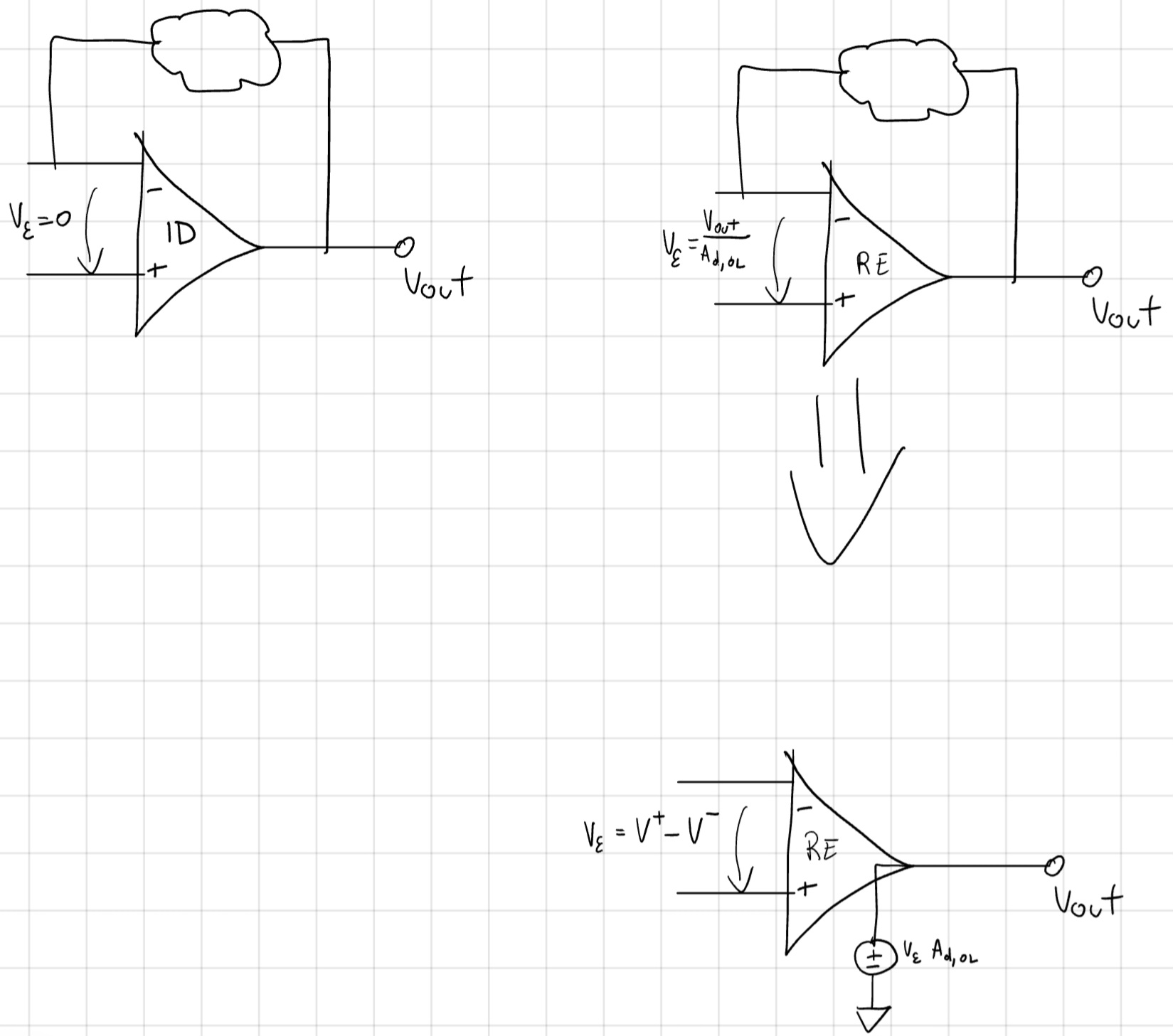
N.B. Se ripetessimo i calcoli con resistenza d’ingresso e d’uscita, notiamo un contributo non nullo a causa di v_\varepsilon \not ={0}
Guadagno di modo comune (open loop) non nullo
Idealmente se abbiamo v_\varepsilon = 0 con v^+ = v^- \not ={0} ovvero v_{CM} \not ={0} e V_{out} = 0, in realtà abbiamo V_{out} \not ={0}.
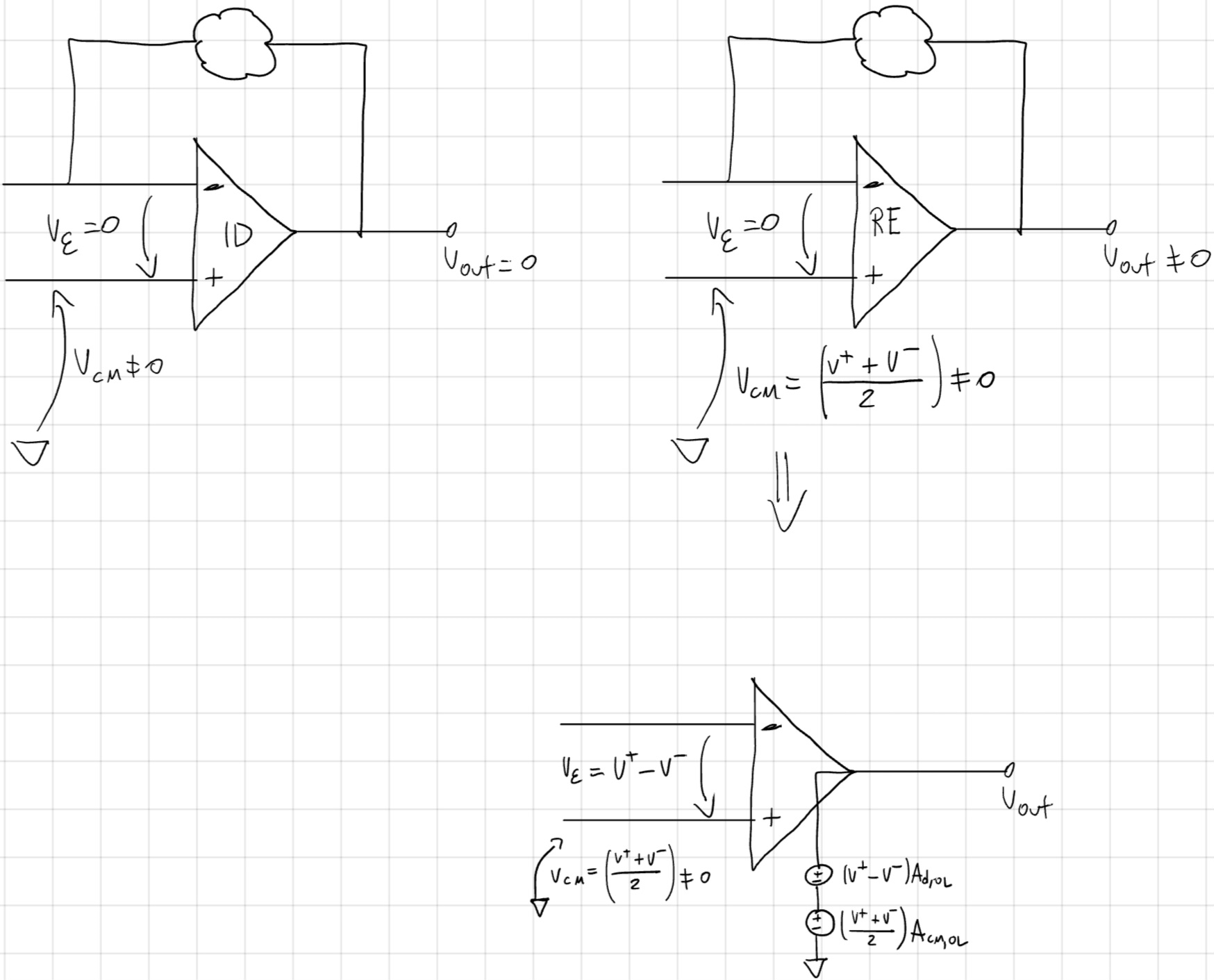
CMRR_{OL} = \frac{A_{d,OL}}{A_{CM,OL}} \\ CMRR_{OL}^{dB} = 10 log_{10} \frac{A^2_{d,OL}}{A^2_{CM,OL}} \\ = 20 log_{10}CMRR_{OL}
N.B. OP= Open-Loop, solitamente viene omesso dal circuito.
Power Supply Rejection Ratio (PSRR)
Idealmente se si ha \varDelta V_{supply} (t) \not ={0} ci aspettiamo V_{out} = 0 se ingresso nullo, in realtà V_{out} \not ={0} e cresce con \varDelta V_{supply}.
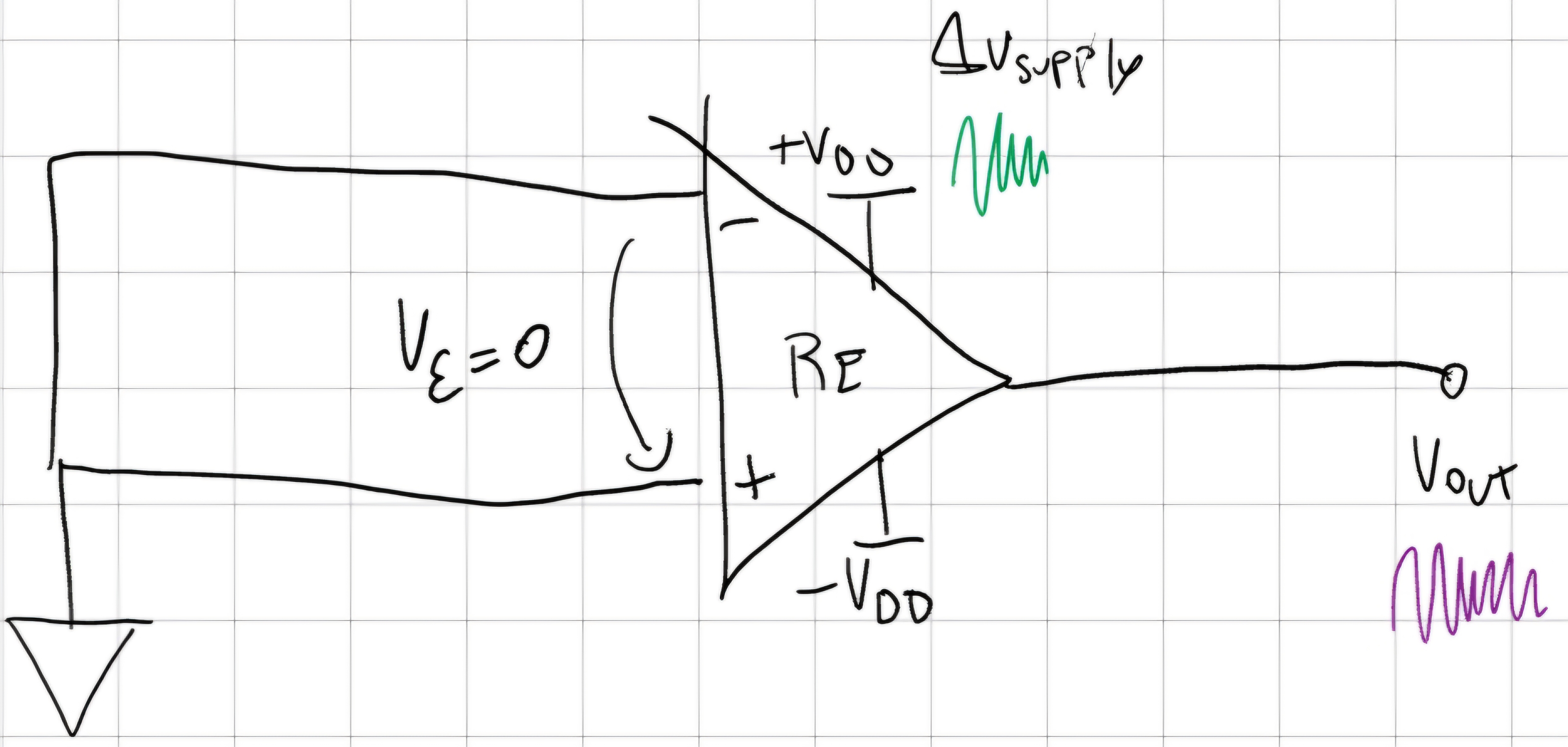
Per usare il modello ideale quindi:
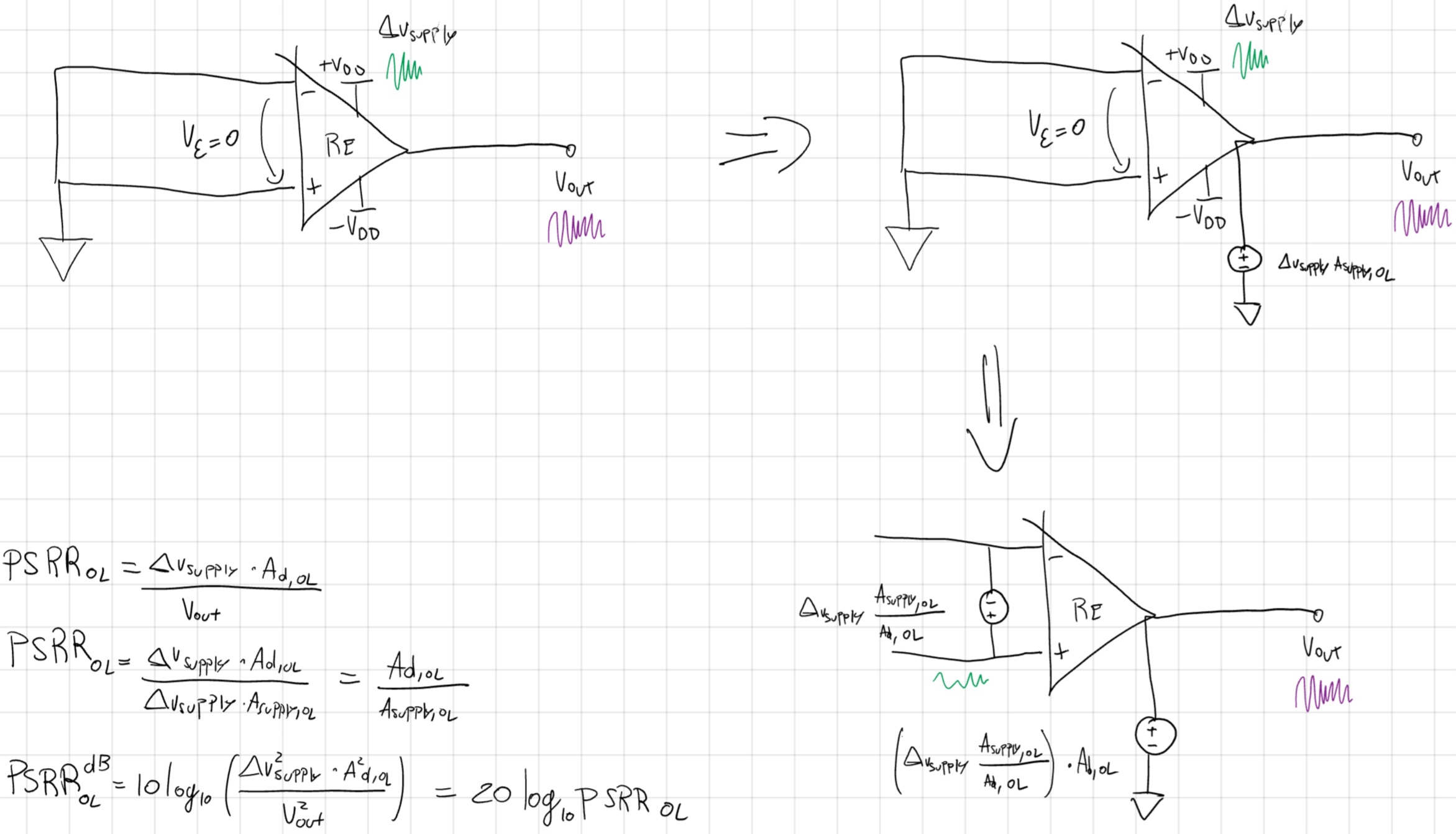
N.B. Ognuno definisce il guadagno differenziale tirando un d20 e/o pescando a caso, quindi chiedere il manuale per scoprire la definizione del giorno.
Od ora parliamo di “Banda Limitata”.
Banda Limitata (AC)
Tutti i guadagni differenziali di modo comune e parassiti sono funzioni di s (FdA).
Quindi ogni frequenza risponde in modo diverso.
Ma nel 90% dei casi:
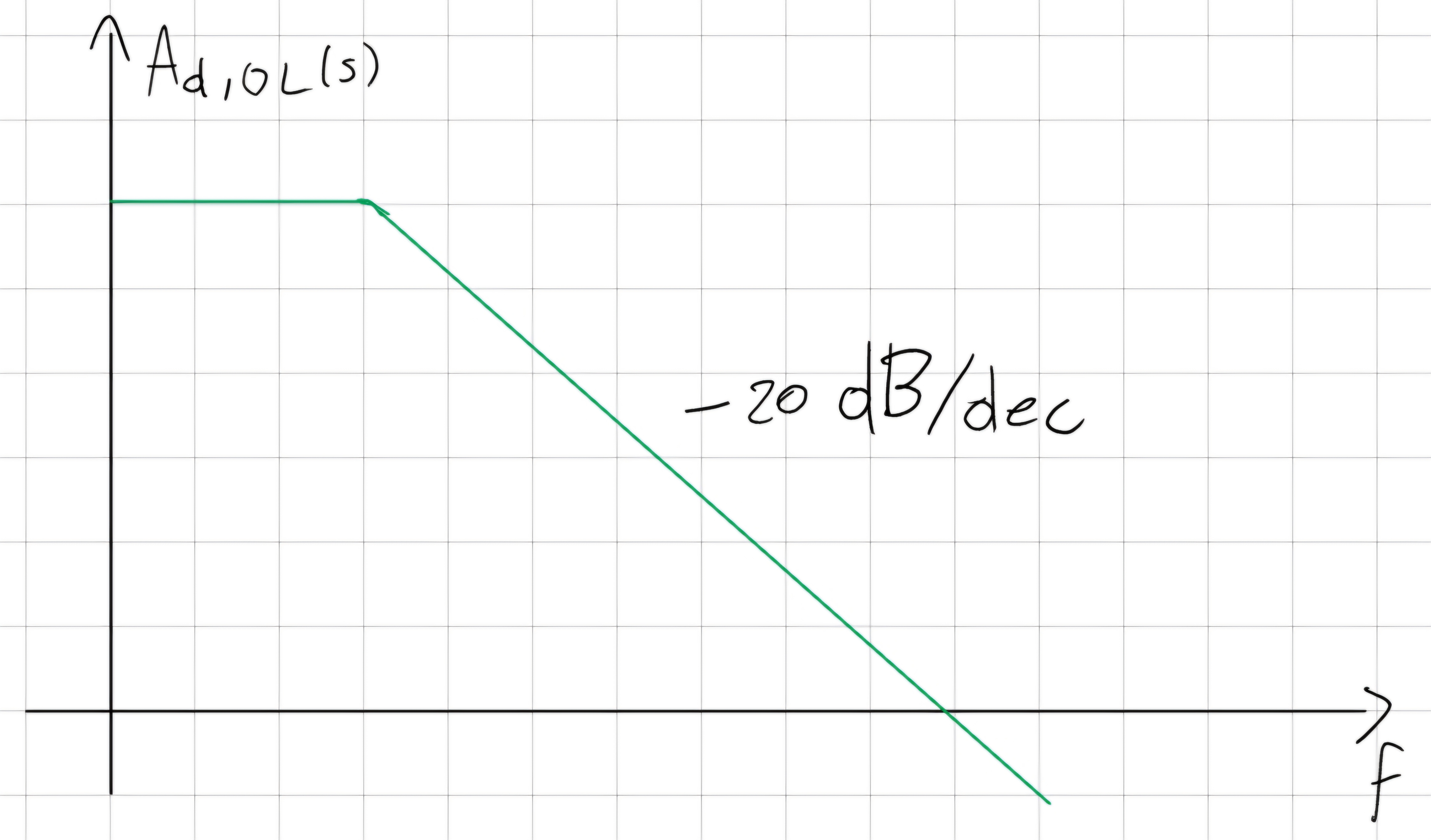
Guida di sopravvivenza per il guadagno differenziale:
- Trascuriamo i contributi di modo comune.
- Le altre NON idealità si valutano sugli OpAmp ideali.
- Il guadagno differenziale finito e la relativa banda si tratta con la teoria della retroazione.
Capitolo Nove: Reatroazione (FdA is back)
Ricordo rapido rapido di FdA (guardate su appunti per approfondire).
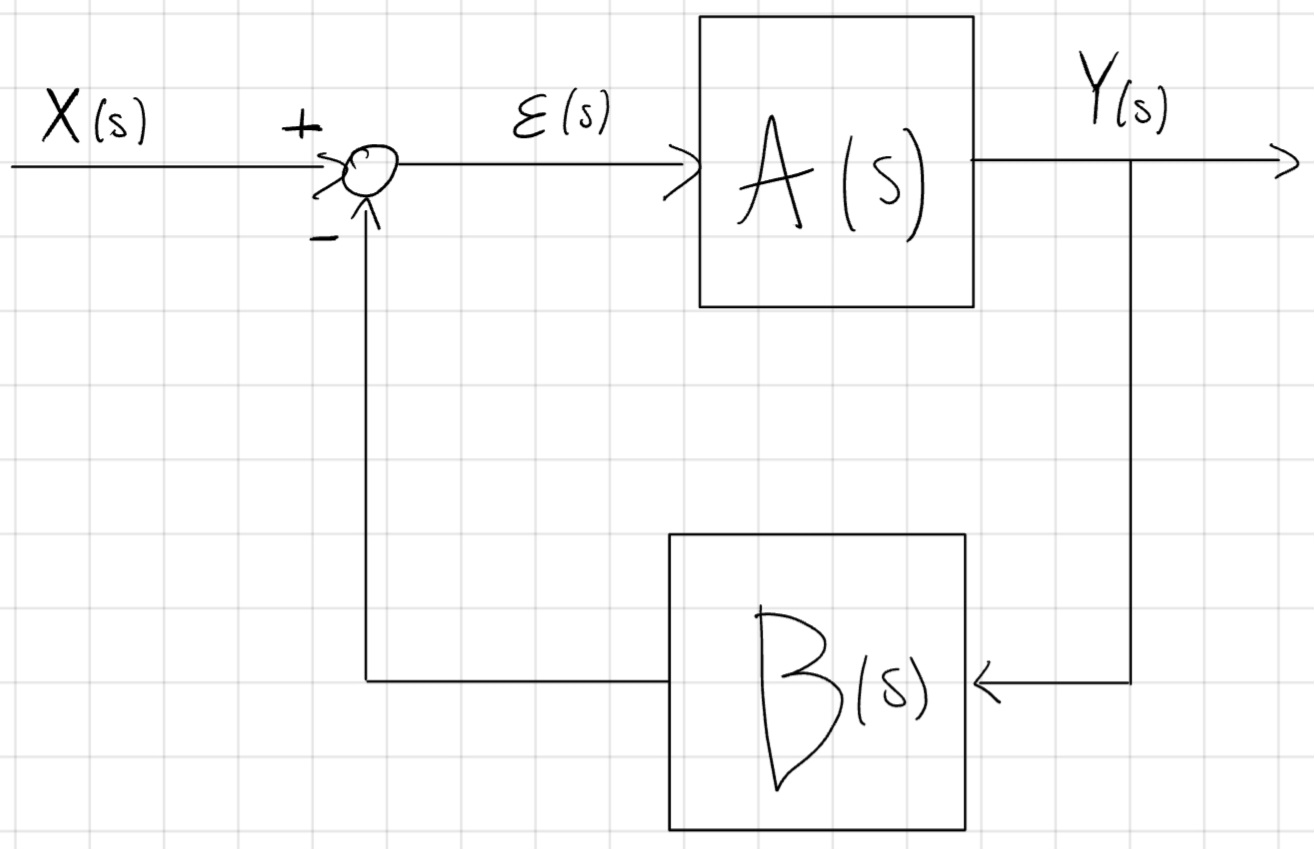
Se unidirezionali:
Y(s) = \varepsilon (s) A(s)
\varepsilon (s) = X(s) - Y(s)B(s)
\frac{Y(s)}{X(s)} = \frac{A(s)}{1 + A(s)B(s)}
\frac{\varepsilon (s)}{X(s)} = \frac{1}{1+ A(s)B(s)}
Funzione d’anello: L(s) = A(s)B(s)
Così da avere una funzione di trasferimento (FdT) indipendente da A ma dipendente da B.
\frac{Y(s)}{X(s)} = \frac{A(s)}{1+A(s)B(s)} \xrightarrow{A \to +\infty} \frac{1}{B(s)} \\ \frac{\partial (\frac{Y(s)}{X(s)})}{\partial A(s)} = \frac{\partial (\frac{A}{1+AB})}{\partial A} = \frac{1(1+AB) - A(B)}{(1+AB)^2} = \frac {1}{(1+AB)^2} \xrightarrow{A \to + \infty} 0 \\ \frac{\partial (\frac{Y(s)}{X(s)})}{\partial B(s)} = \frac{\partial (\frac{A}{1+AB})}{\partial B} = \frac{0(1+AB) - A(A)}{(1+AB)^2} = \frac{A^2}{(1+AB)^2} \xrightarrow{A \to + \infty} 1
Si richia di creare poli instabili.
9.1 Le retroazioni ed Elettronica (una storia d’amore)
Cosa è semplice fare in elettronica ?
- Fare amplificatori a grande guadagno \to A.
- Fare reti passive stabili \to B.
Blocco A
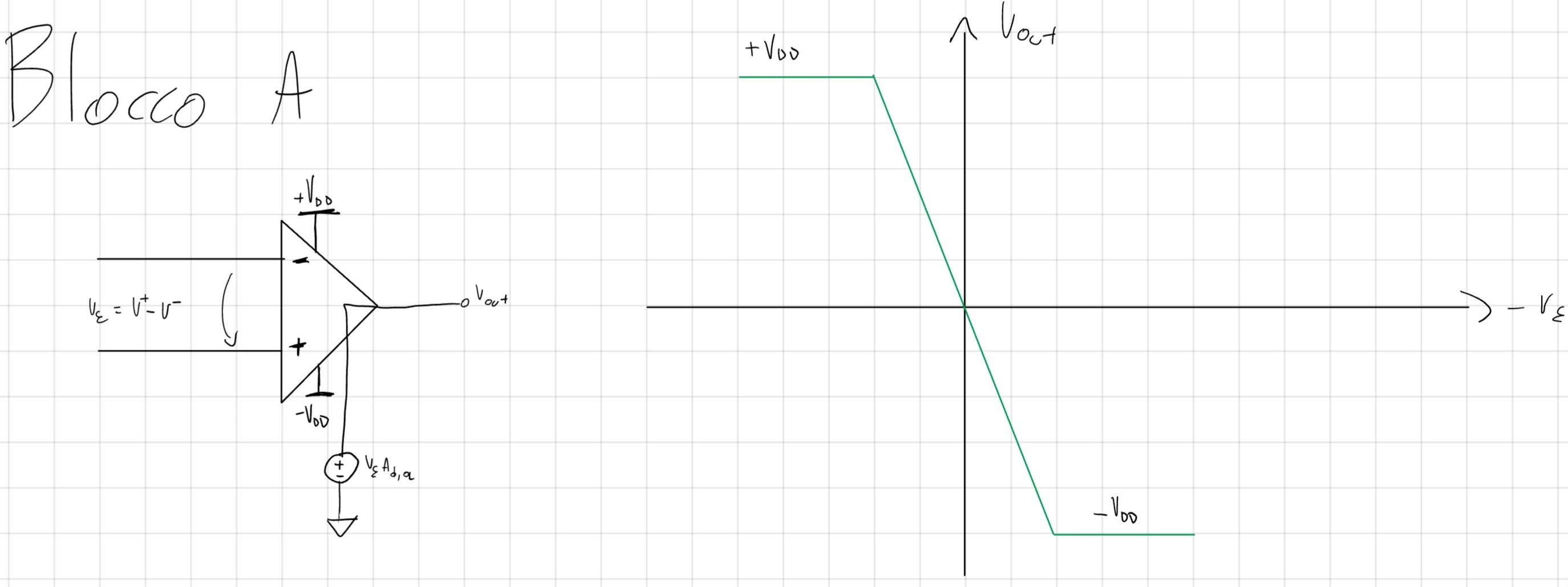
Nel blocco A usiamo un OpAmp comune, il generatore di tensione è dipendente.
L’OpAmp notiamo che ha caratteristiche simili all’inverter.
Blocco B
È una qualsiasi rete passiva (R/L/C), che garantisce l’annullamento di v_\varepsilon.
2 tipi:
Annullamento di tensione (non invertente)
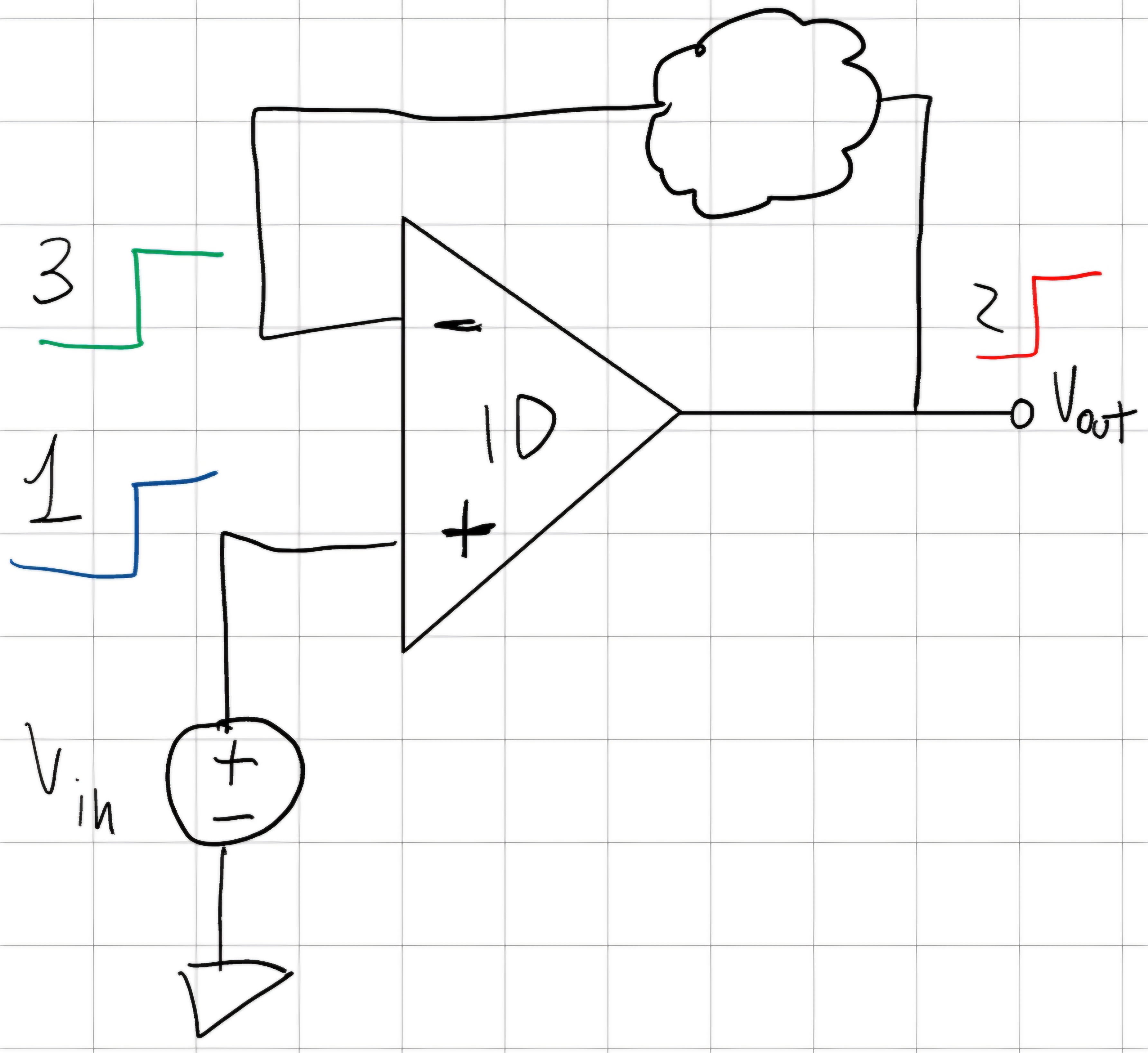
Annullamento in corrente (INVERTENTE)
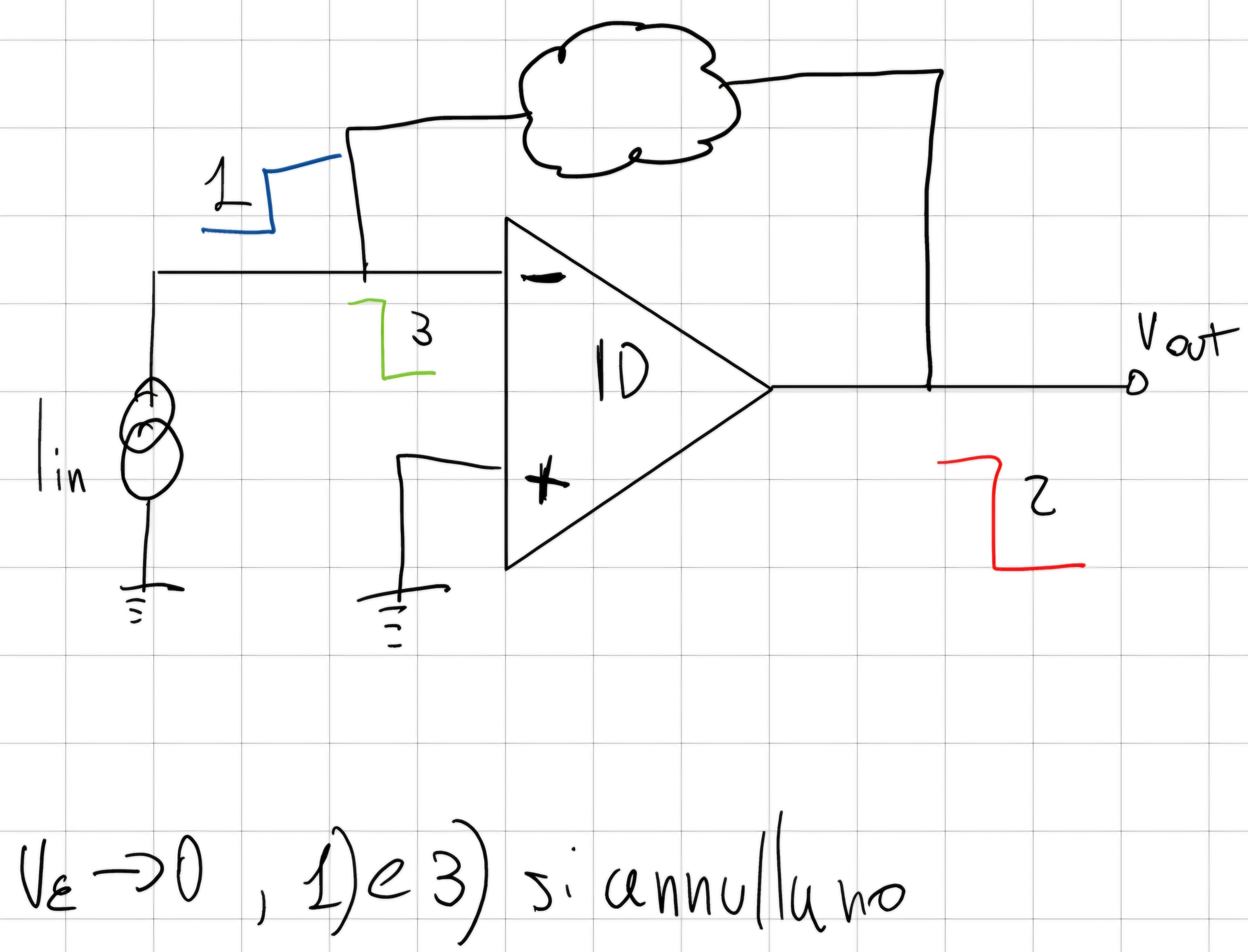
9.2 Il G_{Loop}
In elettronica risulta più pratico valutare il “guadagno d’Anello” (G_{Loop}):
G_{Loop} (s) = -A(s)B(s) = -L(s)
N.B. Essendo la rete B passiva, non è unidirezionale.
Esempio
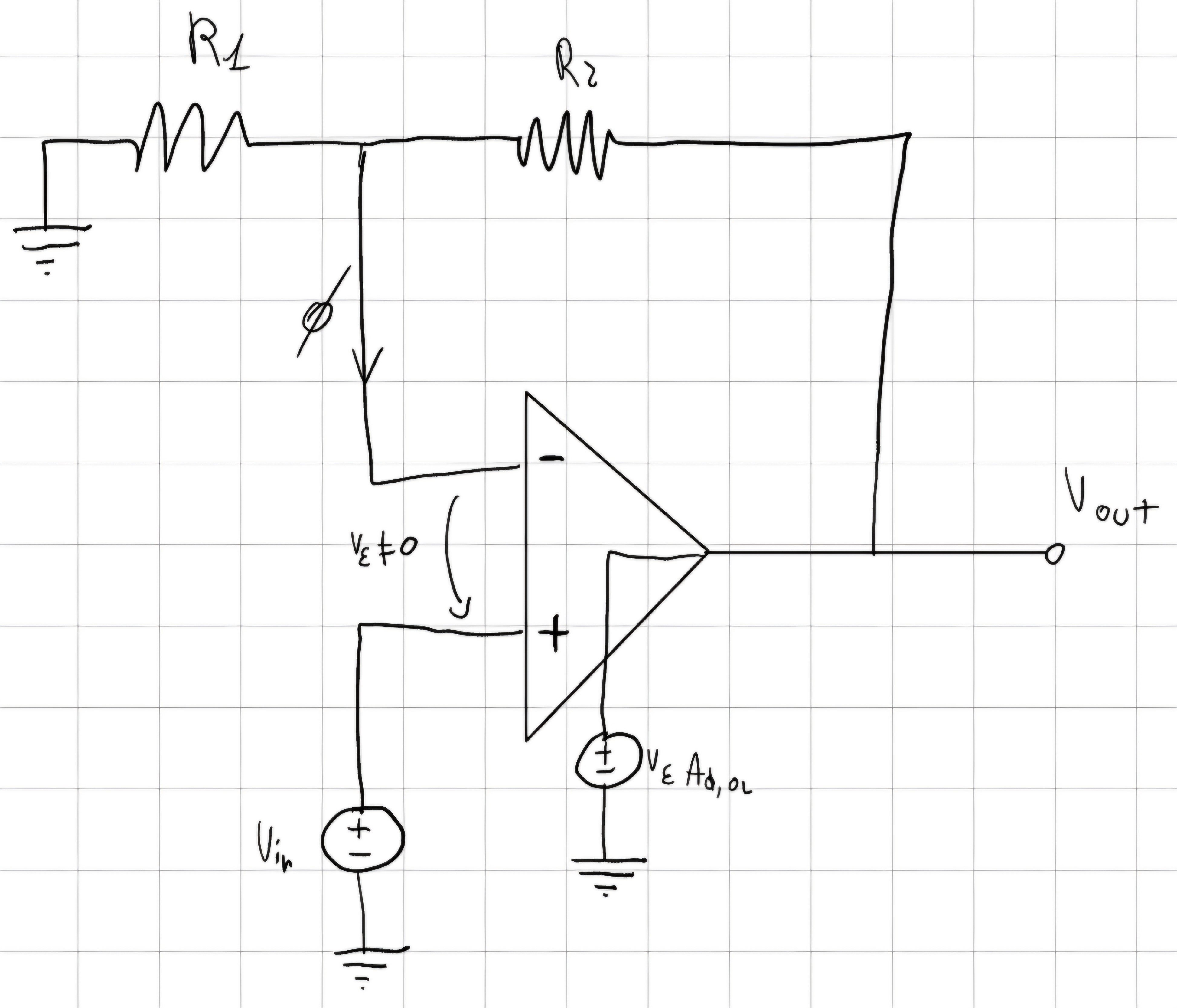
v_\varepsilon = V_{in} - V_{out}\frac{R_1}{R_1 + R_2} \\ V_{out} = v_\varepsilon A_{d,OL} \\ \frac{V_{out}}{A_{d,OL}} = V_{in} - V_{out}\frac{R_1}{R_1+R_2} \\ V_{out}(\frac{1}{A_{d,OL}}+\frac{R_1}{R_1+R_2}) = V_{in} \\ \frac{V_{out}}{V_{in}} = \frac{1}{(\frac{R_1 + R_2 + R_1 A_{d,OL}}{A_{d,OL}(R_1+R_2)})} = G_{REAL} \\ G_{REAL} = \frac{(R_1 + R_2)A_{d,OL}}{R_1 + R_2 + R_1A_{d,OL}} \\ G_{ID} = 1 + \frac{R_2}{R_1} \\ G_{REAL} = \frac{R_1 + R_2}{R_1} \frac{A_{d,OL}}{\frac{R_1 + R_2}{R_1} + A_{d,OL}} \\ G_{REAL} = G_{ID} \frac{1}{\frac{R_1 + R_2}{R_1}\frac{1}{A_{d,OL}} + 1} = G_{ID} \frac {1}{1 + \frac{1}{\frac{R_1}{R_1 + R_2}A_{d,OL}}} \\ G_{LOOP} = - \frac{R_1}{R_1 + R_2}A_{d,OL}
Valutiamo il G_{LOOP}:
- Spegnamo gli ingressi, tranne il gen. dipendente.
- Tagliamo l’anello in un punto a caso, ricostruendo l’impedenza equivalente.
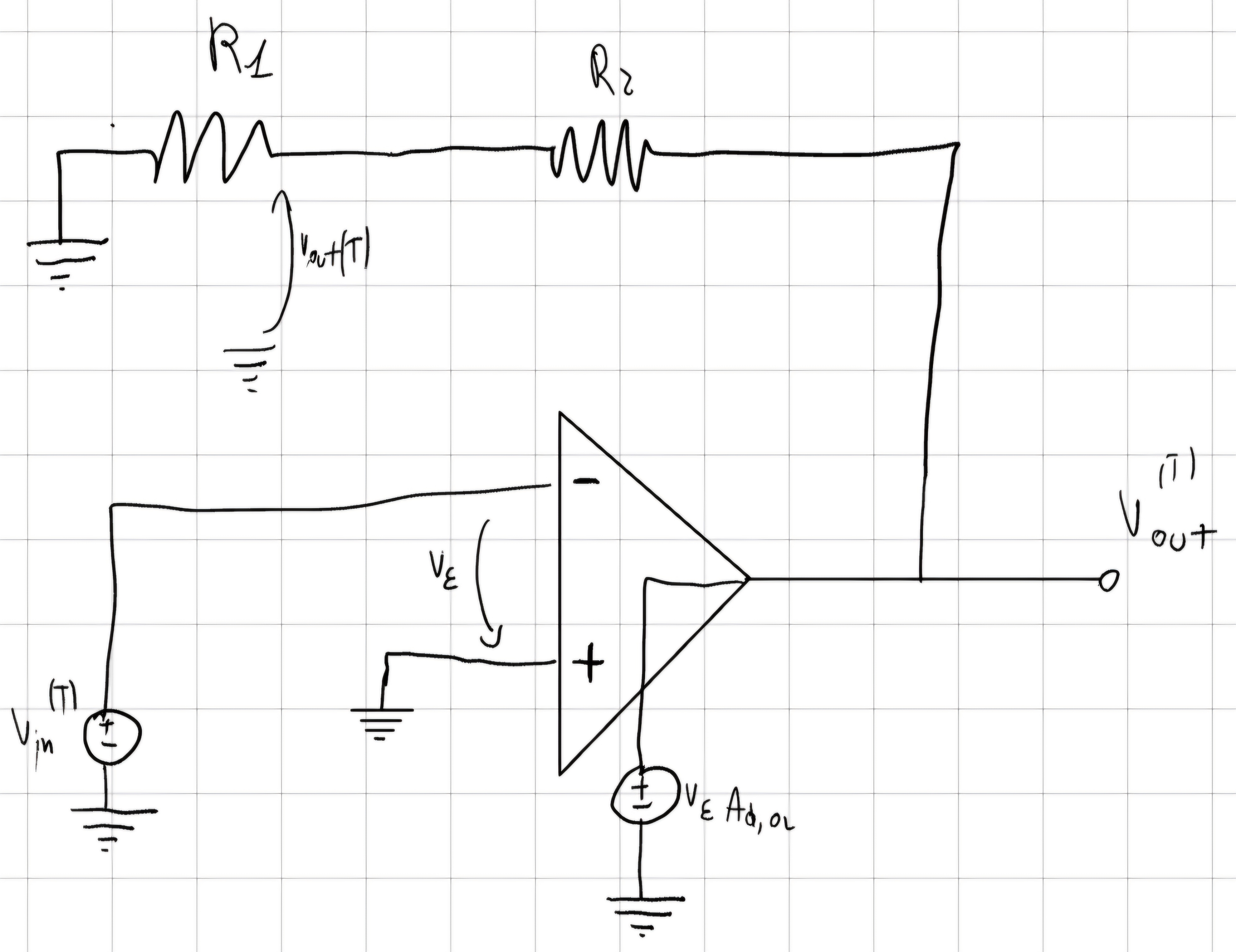
V_{out}^{(T)} = v_\varepsilon^{(T)}A_{d,OL} \\ V_{in}^{(T)} = 0 - v_\varepsilon^{(T)} \\ V_{out}^{(T)} = \frac{R_1}{R_1 + R_2}V_{out}^{(T)} \\ G_{Loop} = \frac{V_{out}^{(T)}}{V_{in}^{(T)}} = - \frac{R_1}{R_1 + R_2}A_{d,OL} \\ G_{REAL} = \frac{G_{ID}}{1+\frac{1}{-G_{Loop}}} \\ G_{REAL} = \frac{-G_{Loop}G_{ID}}{1-G_{Loop}} \\ G_A = -G_{Loop}G_{ID}
Dunque:
- G_{ID} = 1 + \frac{R_2}{R_1}
- G_{LOOP} = -L(s) = - \frac{R_1}{R_1 + R_2}A_{d,OL}
G_{REAL} = \frac{G_{ID}}{1 + \frac{1}{-G_{LOOP}}} = \frac{-G_{LOOP}G_{ID}}{1 - G_{LOOP}}:
- se |G_{LOOP}| >>1 G_{REAL} \cong G_{ID}.
- se |G_{LOOP}| < 1 G_{REAL} \cong -G_{ID}G_{LOOP} = G_A.
Stabilità
Stesse cose di FdA solo che G_{LOOP} = -L(s) quindi:
- G_{LOOP} deve essere <0.
- Nel margine di fase usiamo -180° come riferimento non 0°.
9.3 Ricostruzione dell’Impedenza
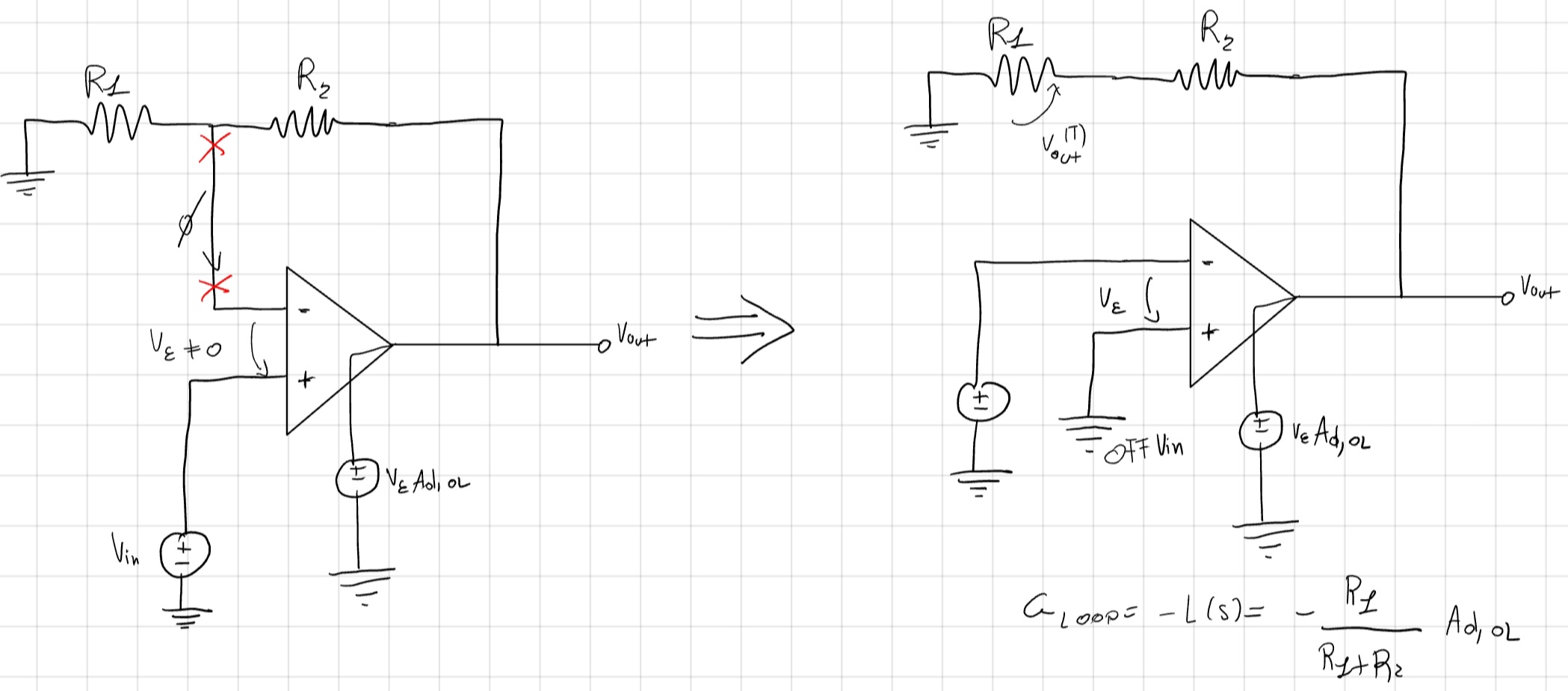
Tagliamo un ramo da cui non scorre corrente.
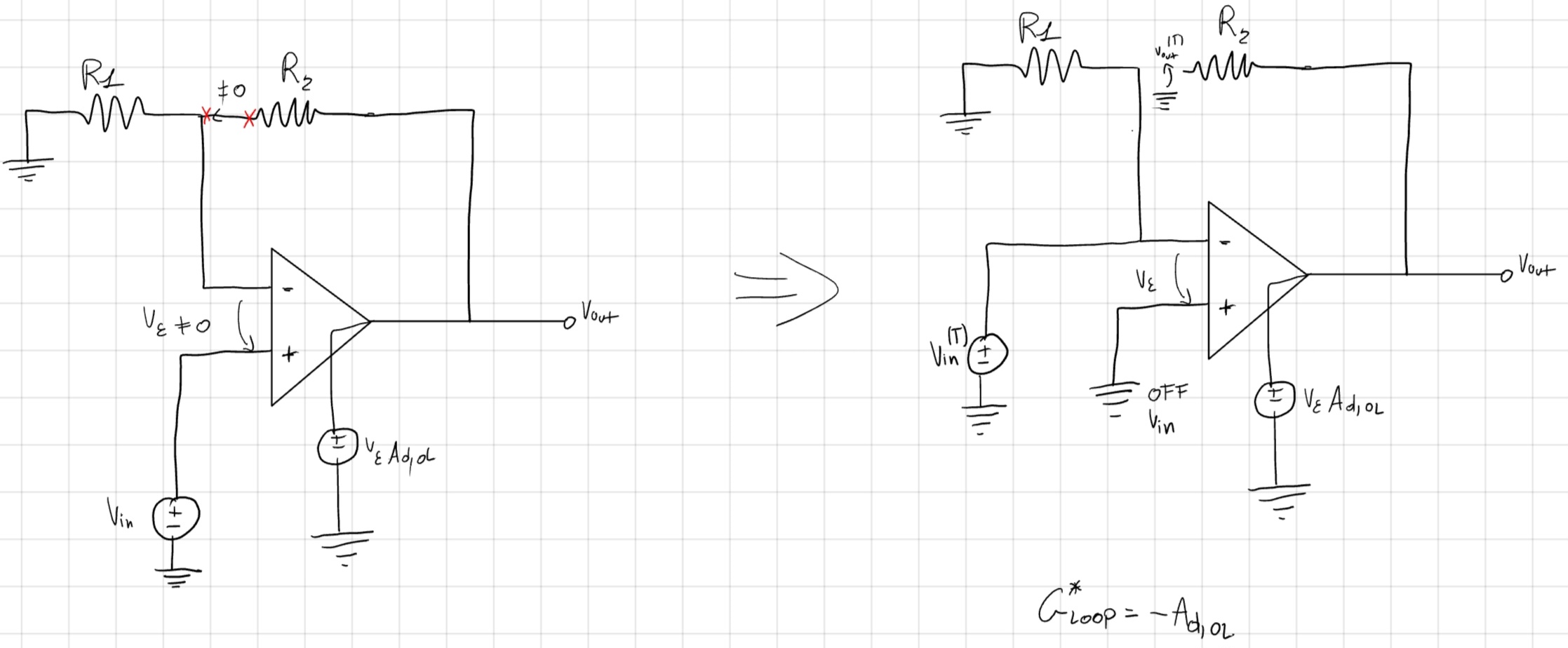
Tagliamo un ramo con corrente.
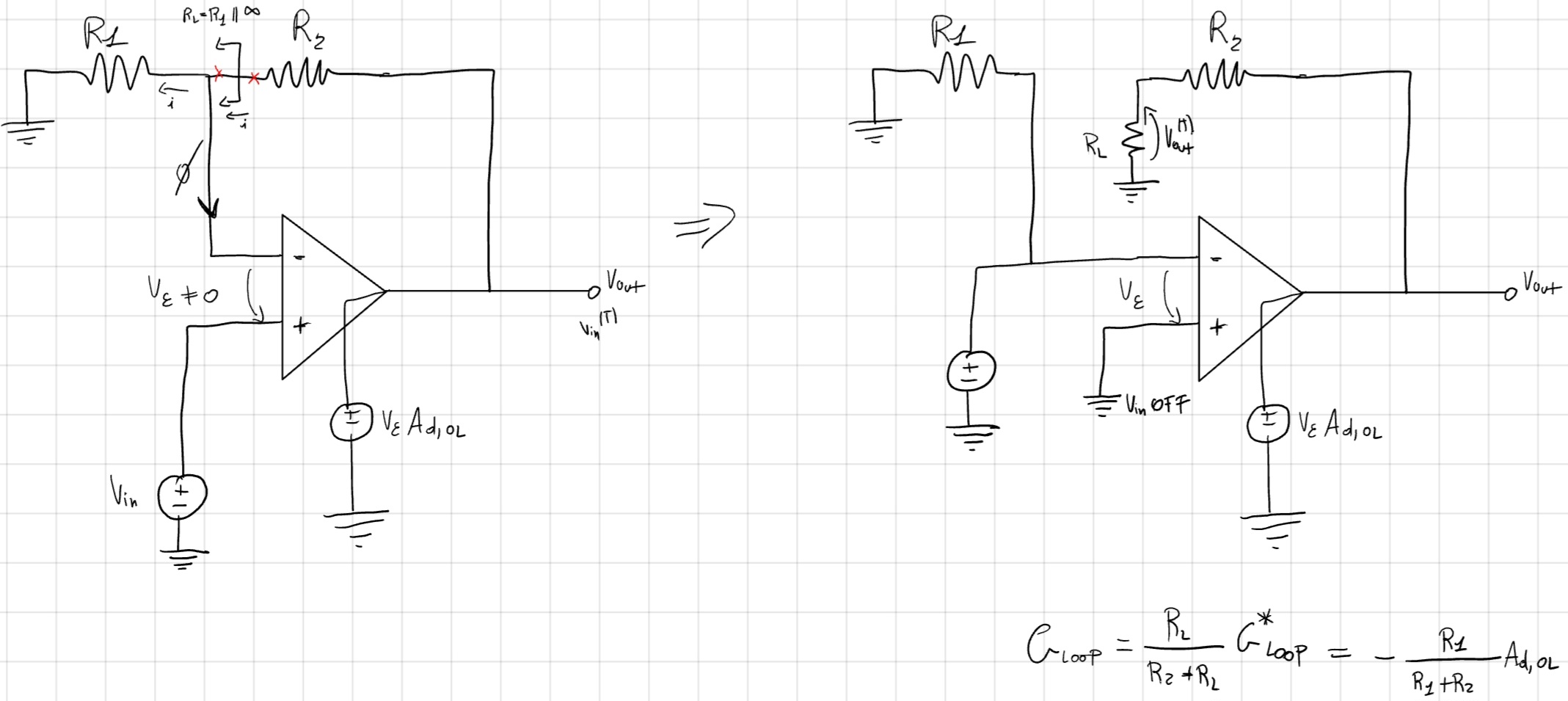
- Dobbiamo ricostruire l’impedenza dove si taglia guadagno nel verso della retroazione.
- Se nel ramo tagliato NON scorre corrente l’impedenza da ricostruire sarà infinita.
- Se tagliamo su un generatore di tensione, l’impedenza ricostruita verrà mascherata dal generatore stesso.
3 Casi:
- Impedenza d’ingresso
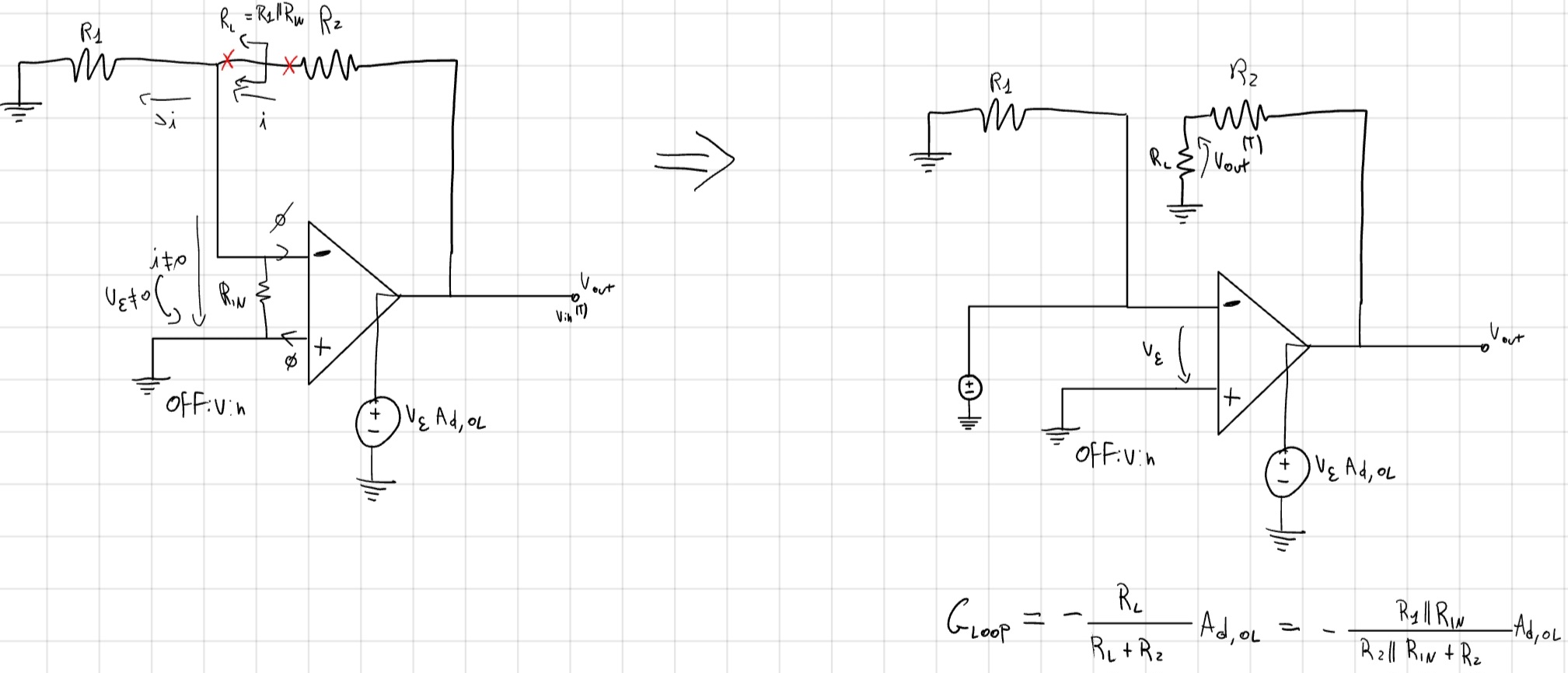
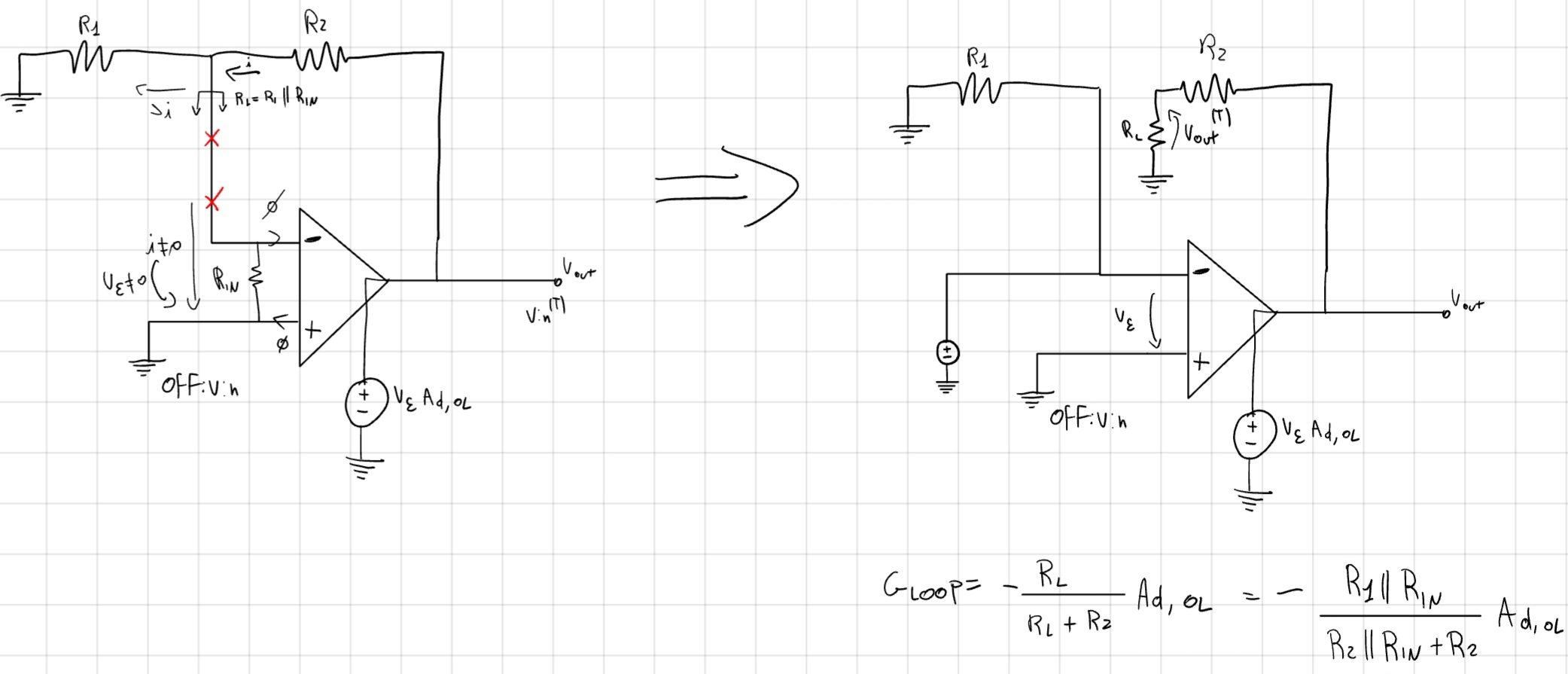
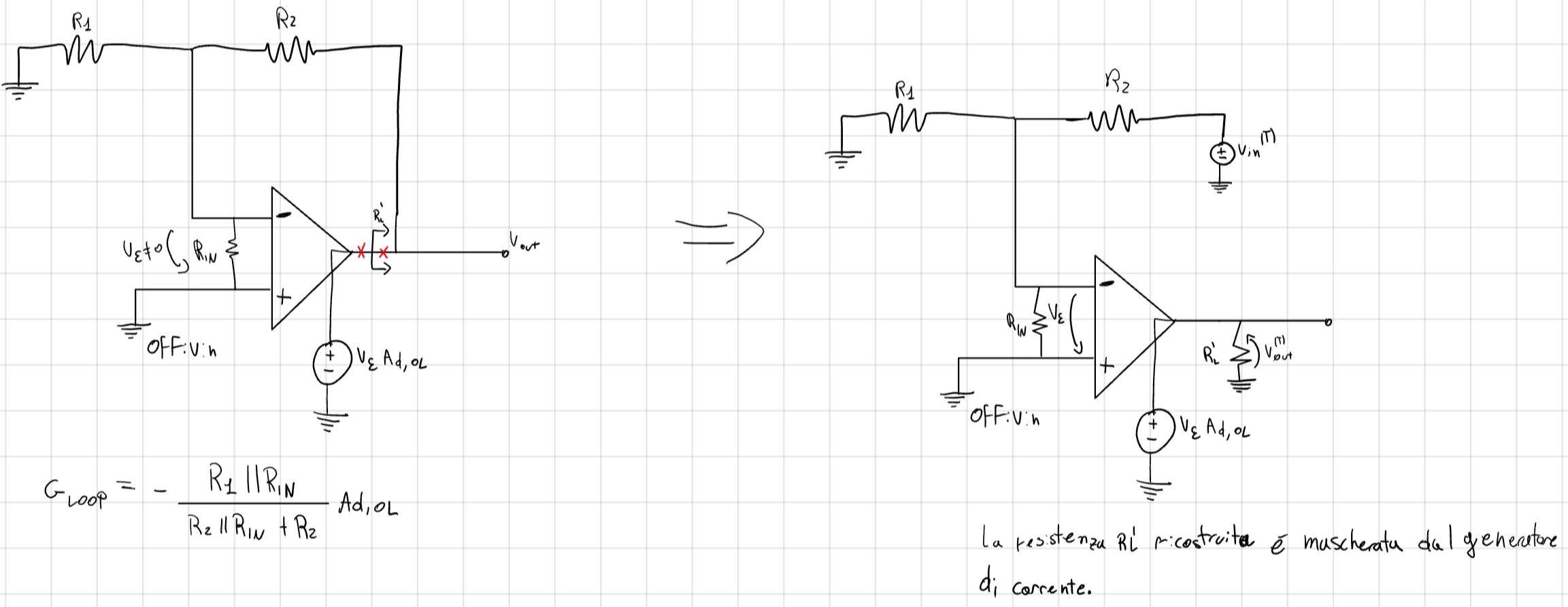
- Impedenza d’uscita
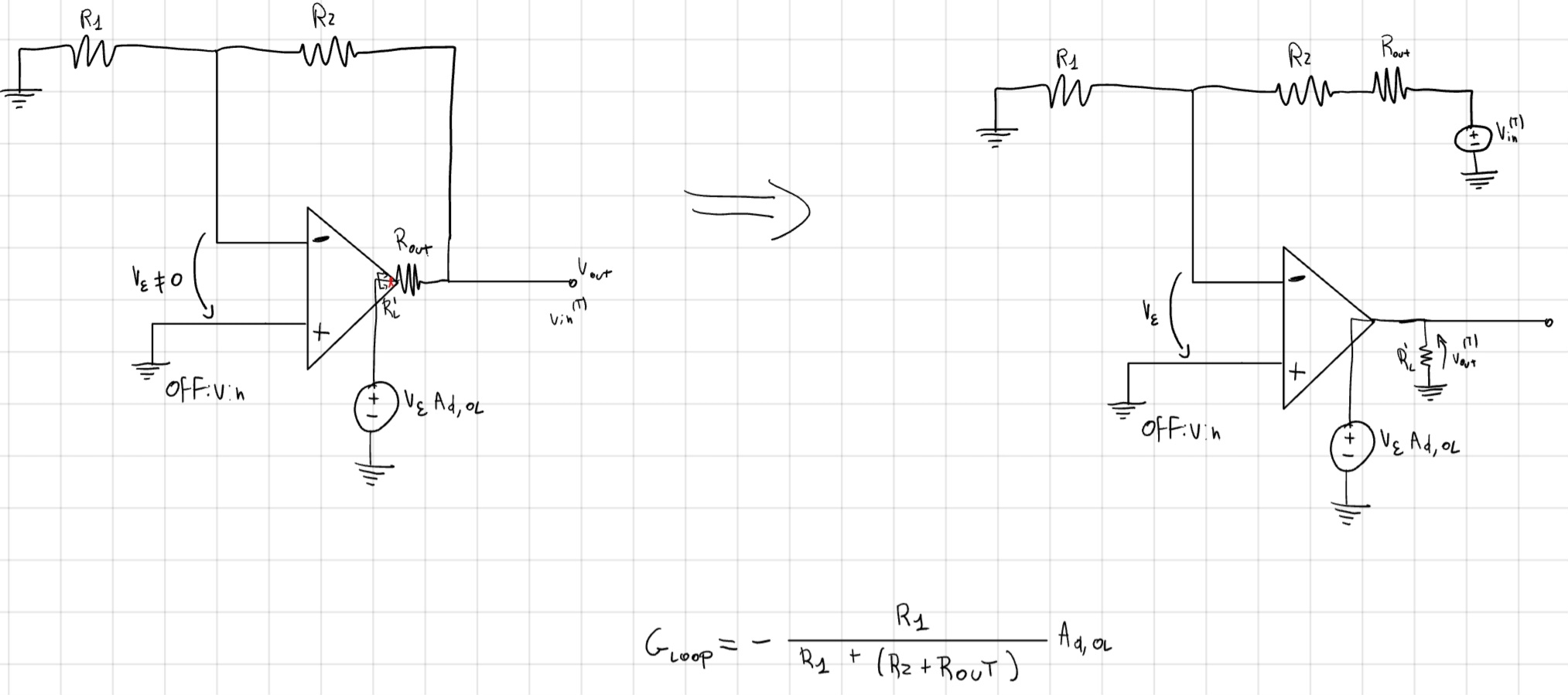
- Impedenza d’uscita ed ingresso
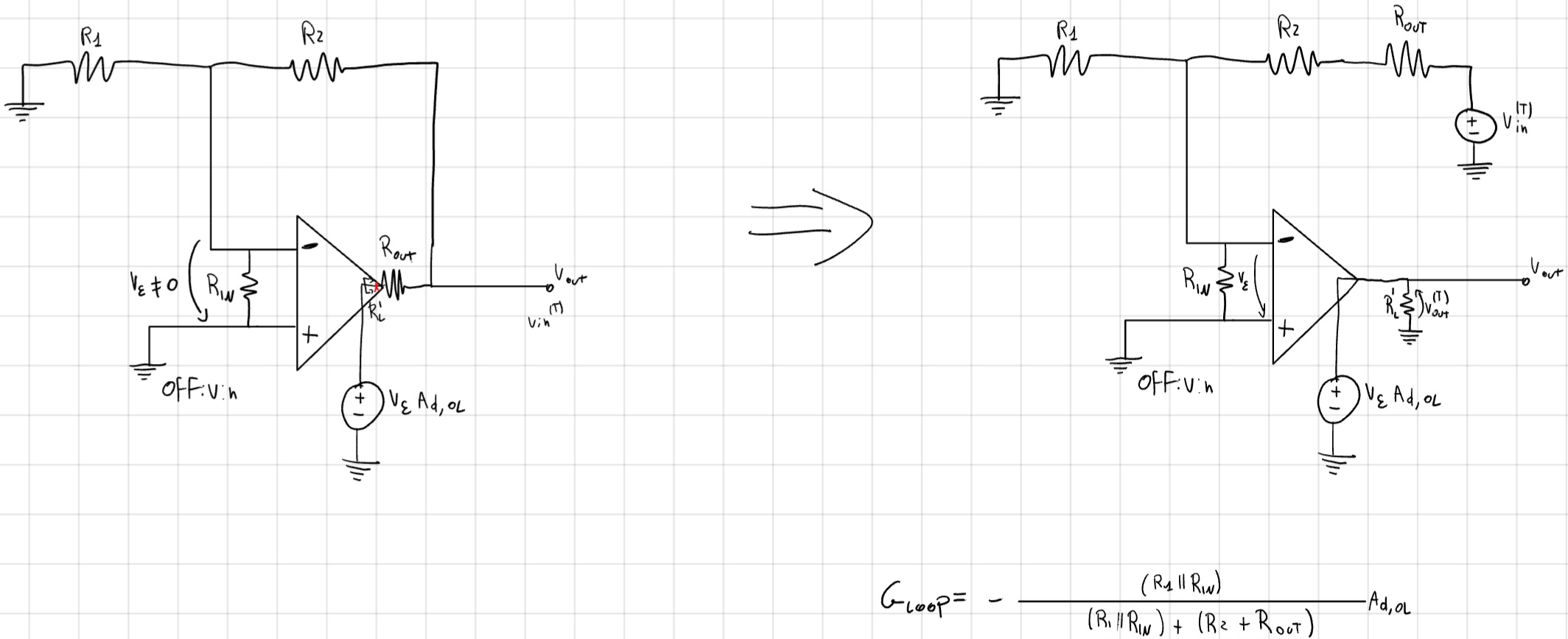
Il G_{LOOP} cambia anche le resistenze:
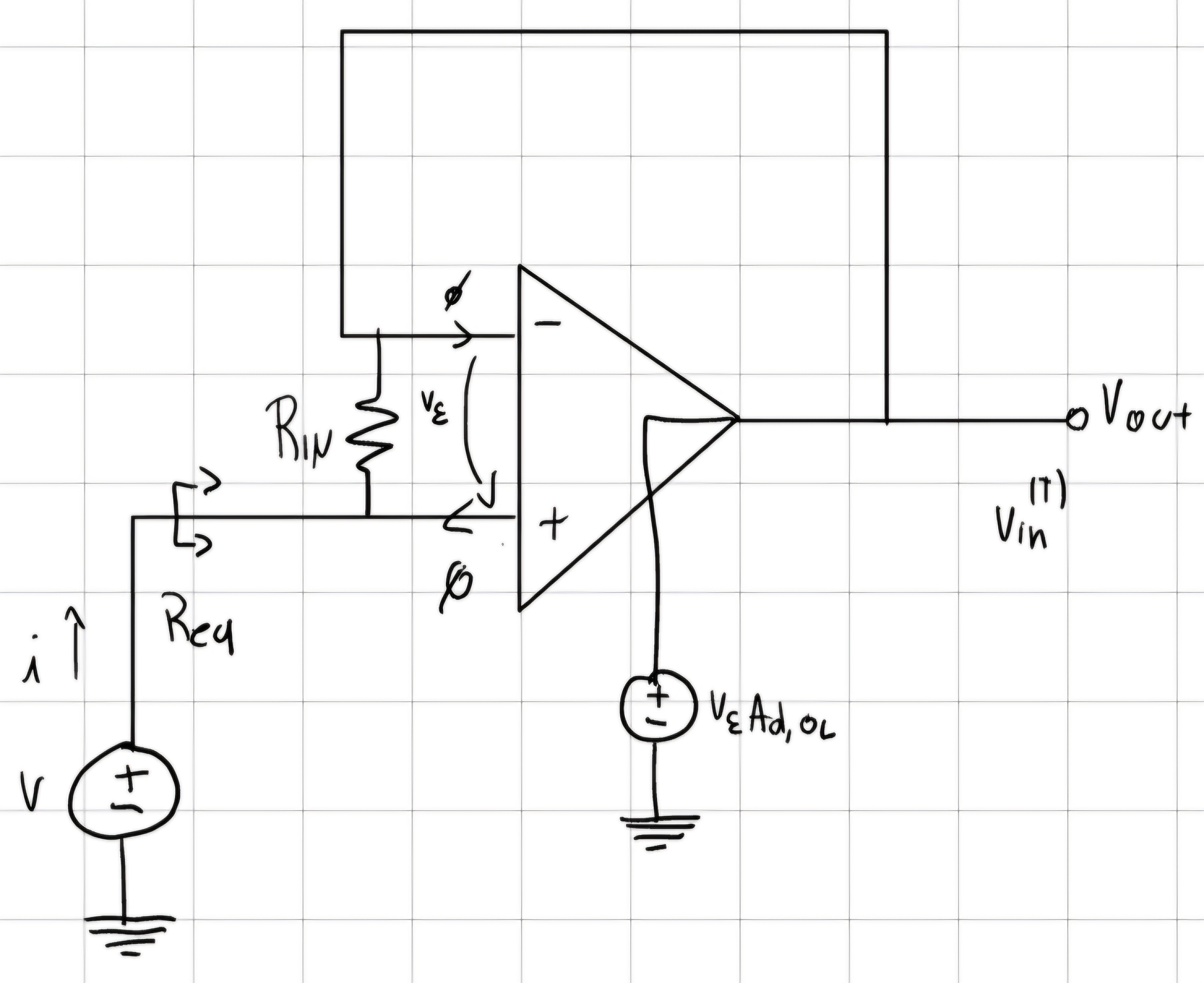
R_{eq} = \frac{v}{i} \\ v_\varepsilon = v - V_{out} \\ V_{out} = v_\varepsilon A_{d,OL} \\ i = \frac{v_\varepsilon}{R_{IN}} \\ v = R_{IN} i + R_{IN} i A_{d,OL} \\ R_{eq} = \frac{v}{i} = R_{IN}(1 - G_{LOOP})
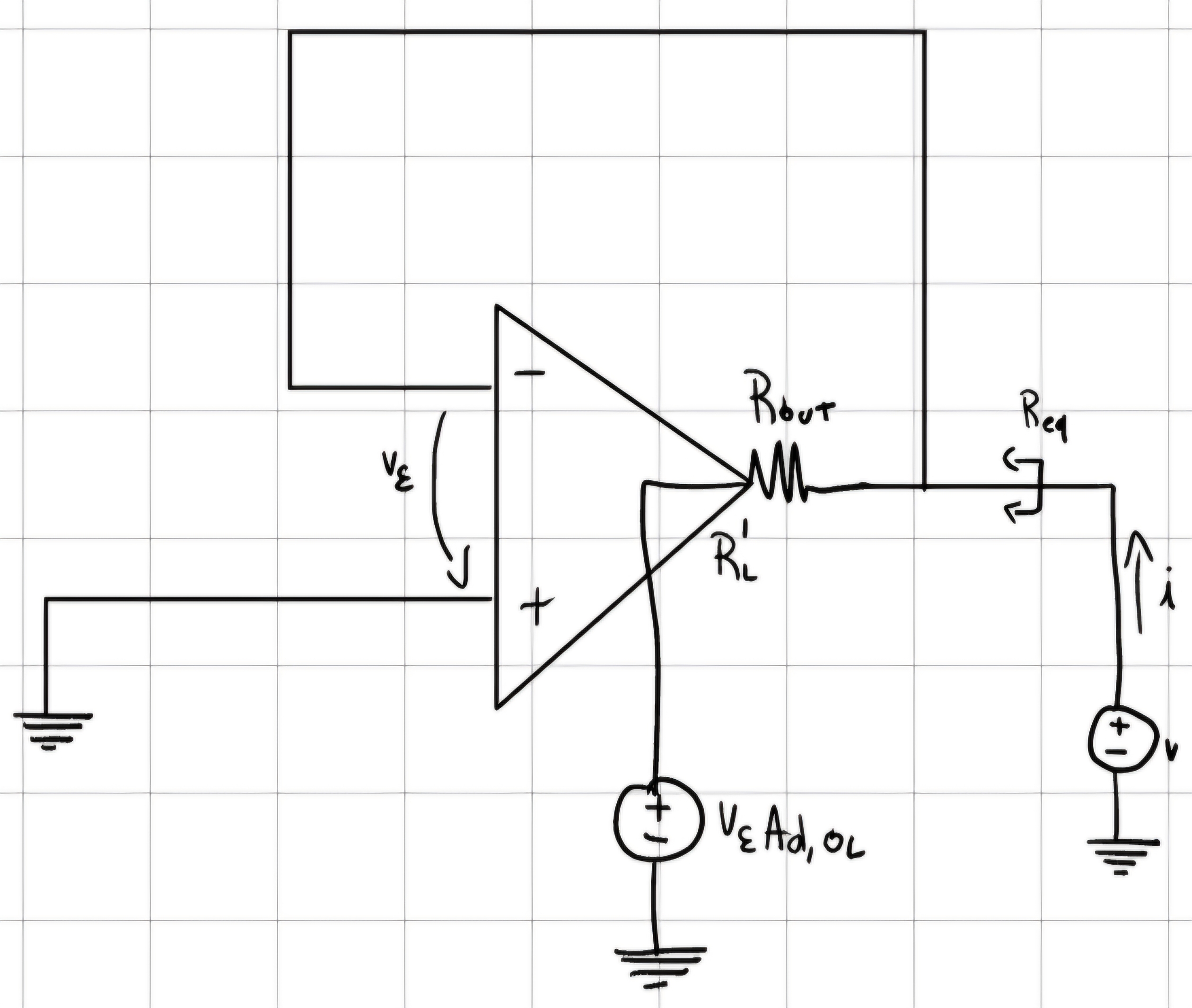
R_{eq} = \frac{v}{i} \\ v_\varepsilon = -v \\ i = \frac {v - v_\varepsilon A_{d,OL}}{R_{OUT}} \\ \frac{i}{v} = \frac{1 + A_{d,OL}}{R_{OUT}} \\ R_{eq} = \frac{v}{i} = \frac{R_{OUT}}{(1-G_{LOOP})}
9.4 Analisi in Frequenza
Se dalla DC ci spostiamo in AC.
G_{REAL} (s) = \frac{- G_{LOOP} (s) G_{ID} (s)}{1 - G_{LOOP} (s)}:
- Se |G_{LOOP} (s)| >> 1 \implies G_{REAL} (s) \cong G_{ID}(s)
- Se |G_{LOOP} (s)| < 1 \implies G_{REAL} (s) \cong - G_{LOOP}(s)G_{ID}(s)
Analisi in frequenza (\beta)
Possiamo usare solo diagrammi di Bode.
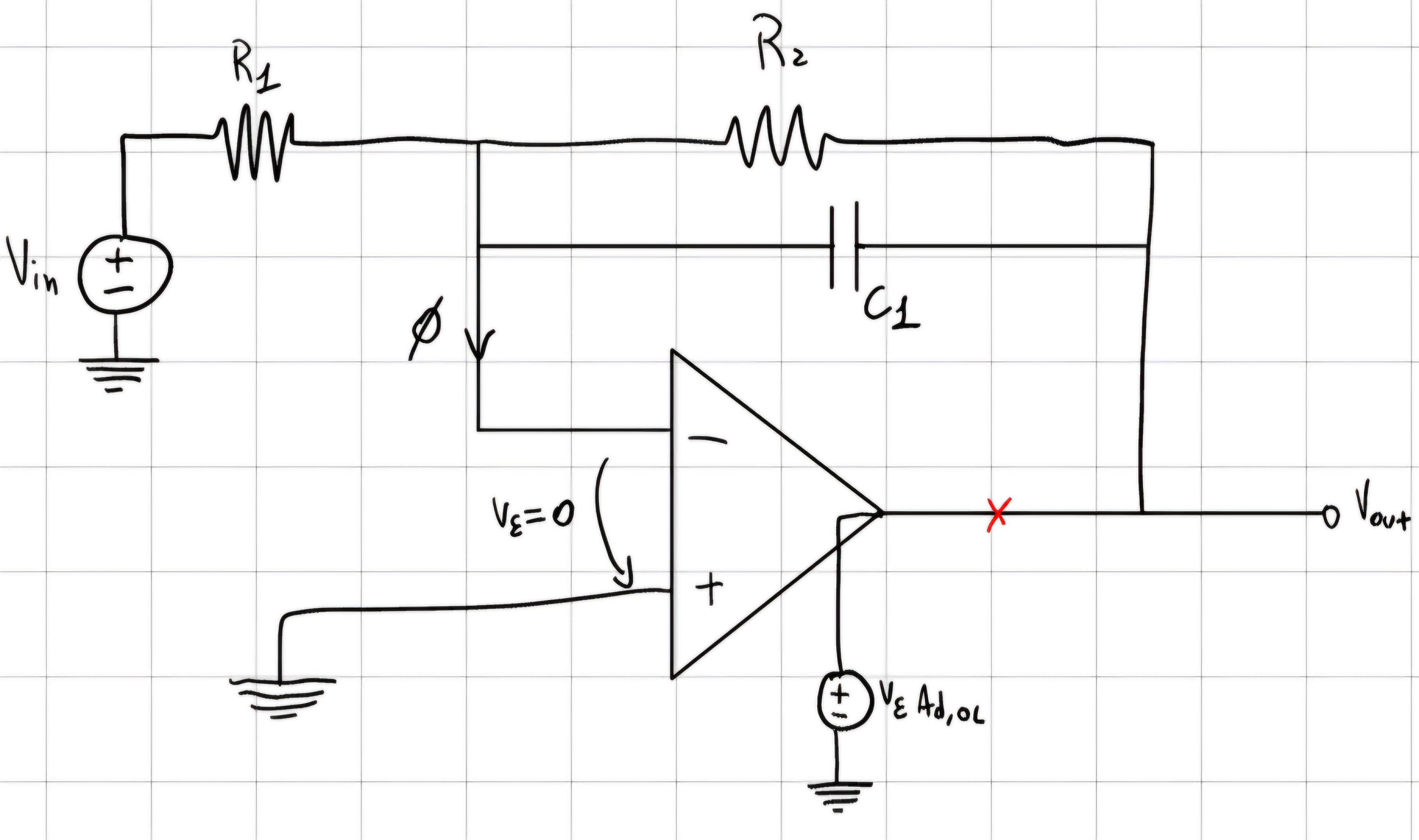
G_{ID}(s) = - \frac{R_2||\frac{1}{sC_1}}{R_1} = -\frac{R_2}{R_1}\frac{1}{1+sC_1R_2} \\ G_{LOOP}(s) = - \frac{R_1}{R_1+R_2||\frac{1}{sC_1}} A_{d,OL} \\ G_{LOOP}(s) = -\frac{R_1}{R_1+\frac{R_2}{1+sC_1R_2}}A_{d,OL} \\ G_{LOOP}(s) = -\frac{R_1(1+sC_1R_2)}{R_1+R_2+sC_1R_1R_2}A_{d,OL} \\ G_{LOOP}(s) = -\frac{R_1}{R_1+R_2}\frac{1+sC_1R_2}{1+sC_1\frac{R_1R_2}{R_1+R_2}}A_{d,OL} \\ G_{ID} (s) = -\frac{R_2}{R_1}\frac{1}{1+sC_1R_2} \\ G_A(s) = -G_{ID}G_{LOOP} = -\frac{R_2}{R_1+R_2}\frac{A_{d,OL}}{1+sC_1\frac{R_1R_2}{R_1+R_2}}
Sapendo che:
- R_1 < R_2
- \frac{R_1R_2}{R_1+R_2} = R_1||R_2<R_1
- \frac{R_2}{R_1}<<A_{d,OL}
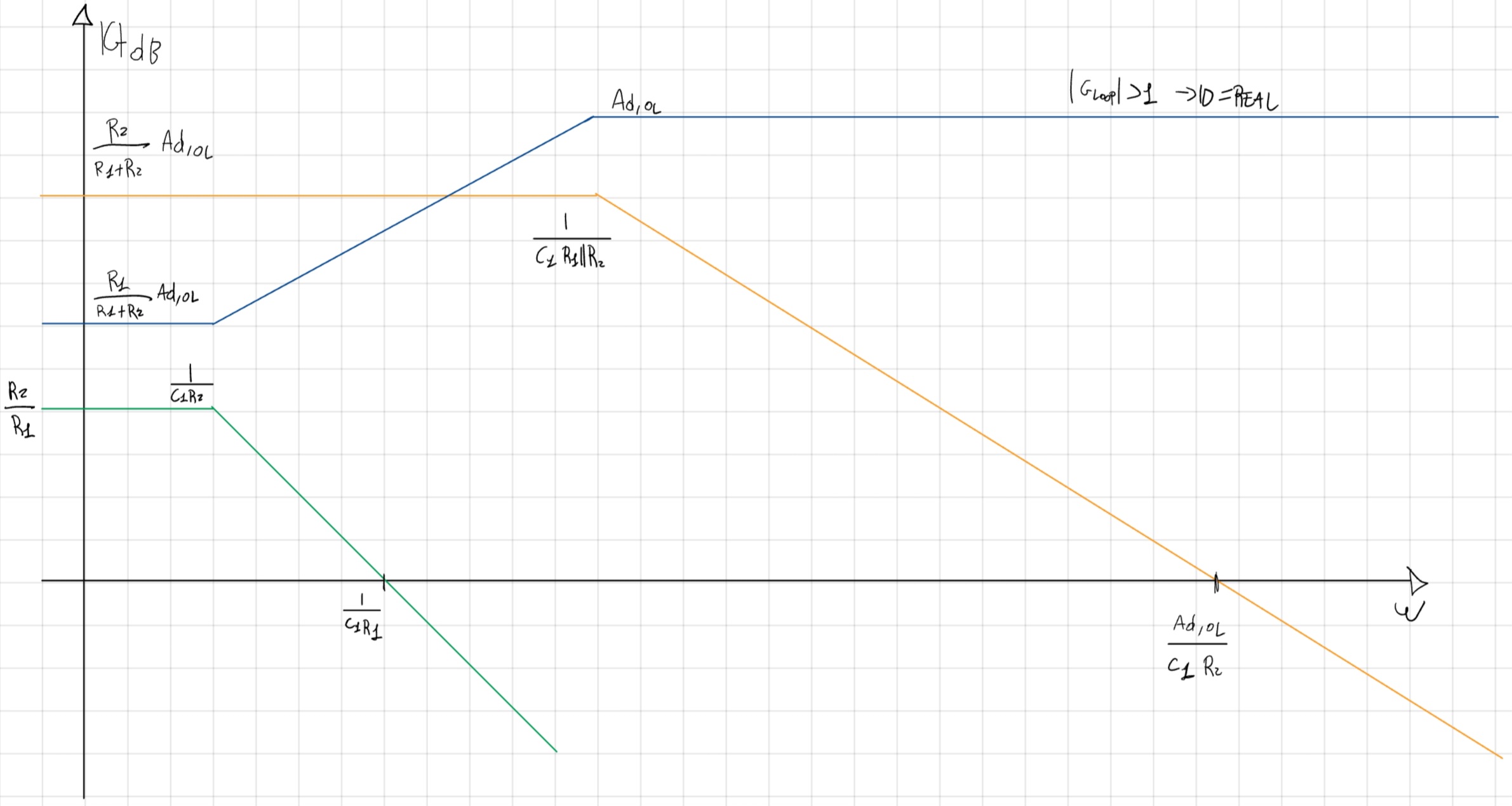
Frequenze \beta non coinvolte.
Analisi in frequenza (\alpha)
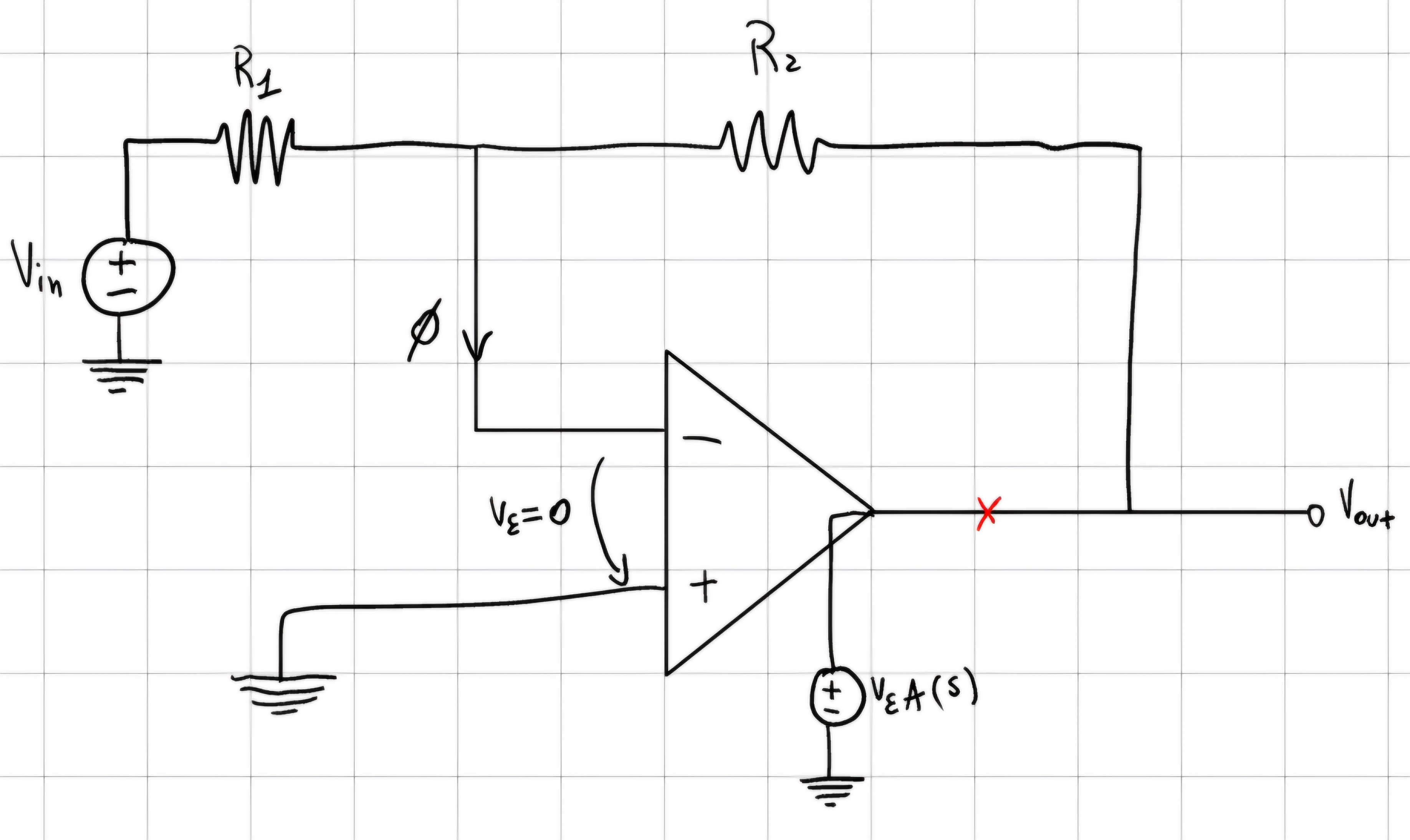
G_{ID}(s) = -\frac{R_2}{R_1} \\ G_{LOOP} (s) = \frac{R_1}{R_1 + R_2}A(s) \\ G_{LOOP}(s) = -\frac{R_1}{R_1+R_2}\frac{A_{d,OL}}{1 + \tau s} \\ G_A(s) = -G_{ID}G_{LOOP} = -\frac{R_2}{R_1 + R_2} \frac{A_{d,OL}}{1 + \tau s}
Sapendo che:
- R_1 < R_2
- \frac{R_1R_2}{R_1 + R_2} = R_1||R_2<R_{1,2}
- \frac{R_2}{R_1}<<A_{d,OL}
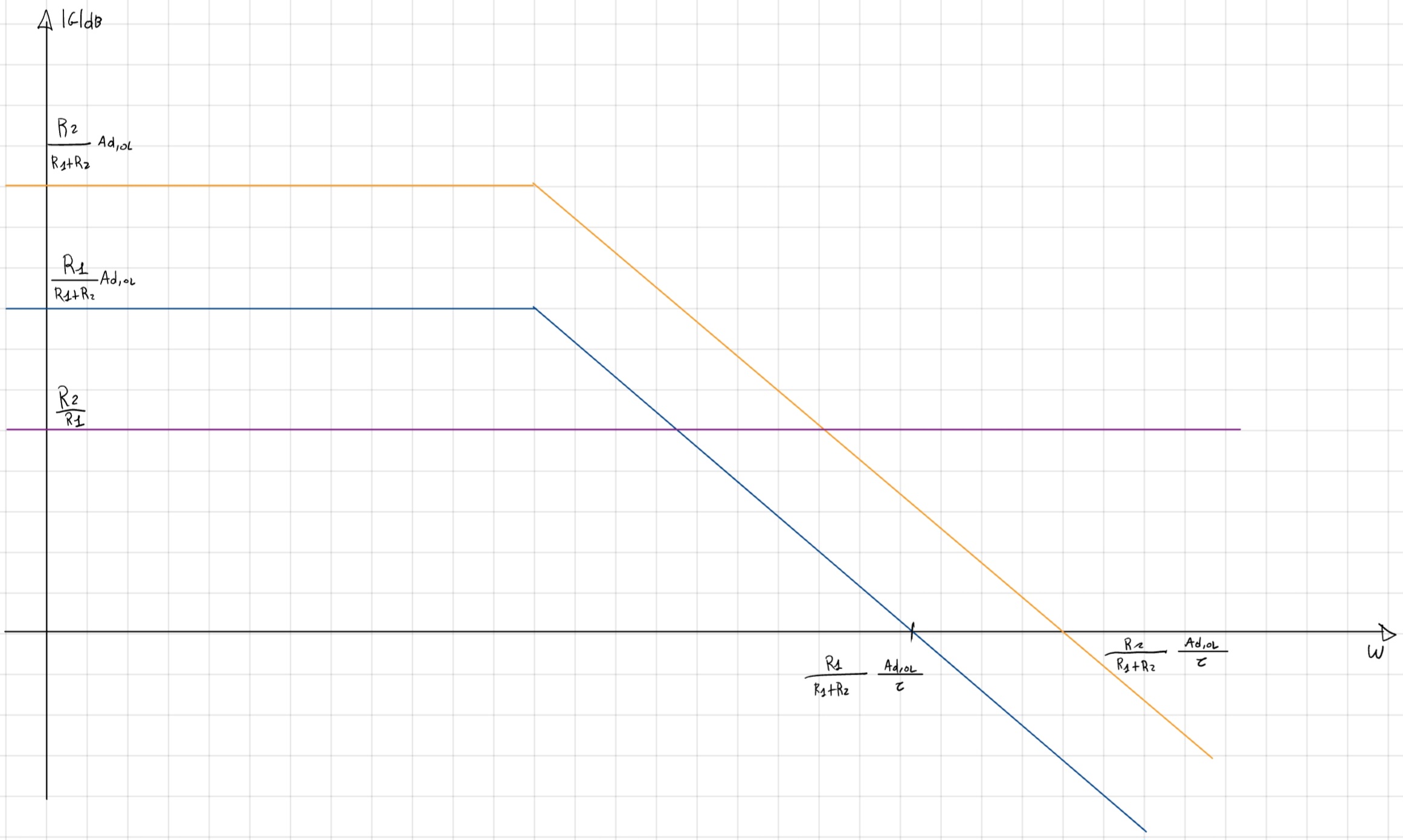
Analisi in frequenza (\alpha + \beta)
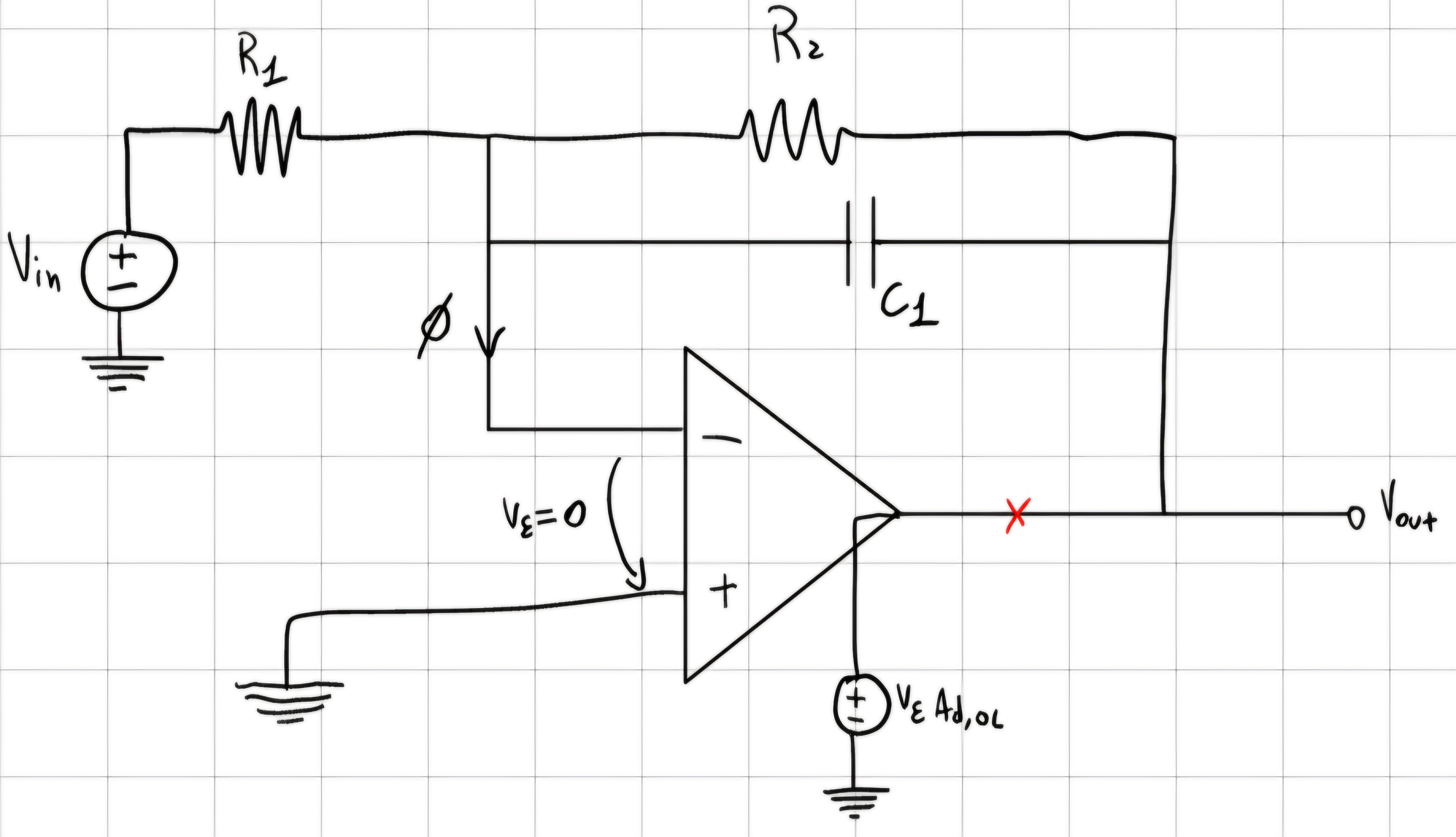
G_{ID}(s) = -\frac{R_2}{R_1}\frac{1}{1+ sC_1R_2} \\ G_{LOOP}(s) = - \frac{R_1}{R_1 + R_2 || \frac{1}{sC_1}}A(s) \\ G_{LOOP}(s) = -\frac{R_1}{R_1 + R_2}\frac{1+sC_1R_2}{1+sC_1\frac{R_1R_2}{R_1 + R_2}}\frac{A_{d,OL}}{1+\tau s} quest’ultima parte richia di portare instabilità.
G_A(s) = -\frac{R_2}{R_1 + R_2}\frac{1}{1 + sC_1\frac{R_1R_2}{R_1 + R_2}}\frac{A_{d,OL}}{1 + \tau s}
Sapendo che:
- R_1 < R_2
- \frac{R_1R_2}{R_1 + R_2} = R_1 || R_2 < R_{1,2}
- \frac{R_2}{R_1} << A_{d,OL}
- \frac{1}{\tau} è la singolarità minore.
Stabilità
IN questa particolare situazione è sufficiente verificare il margine di fase:
- Distanza tra -360° e arg(G_{LOOP}(f)) quando |G_{LOOP}(f)|_{dB} = 0 dB.
- No sovra-elongazione.
- \varphi_m > 45°
- Per sicurezza meglio abbondare a \varphi_m > 60°
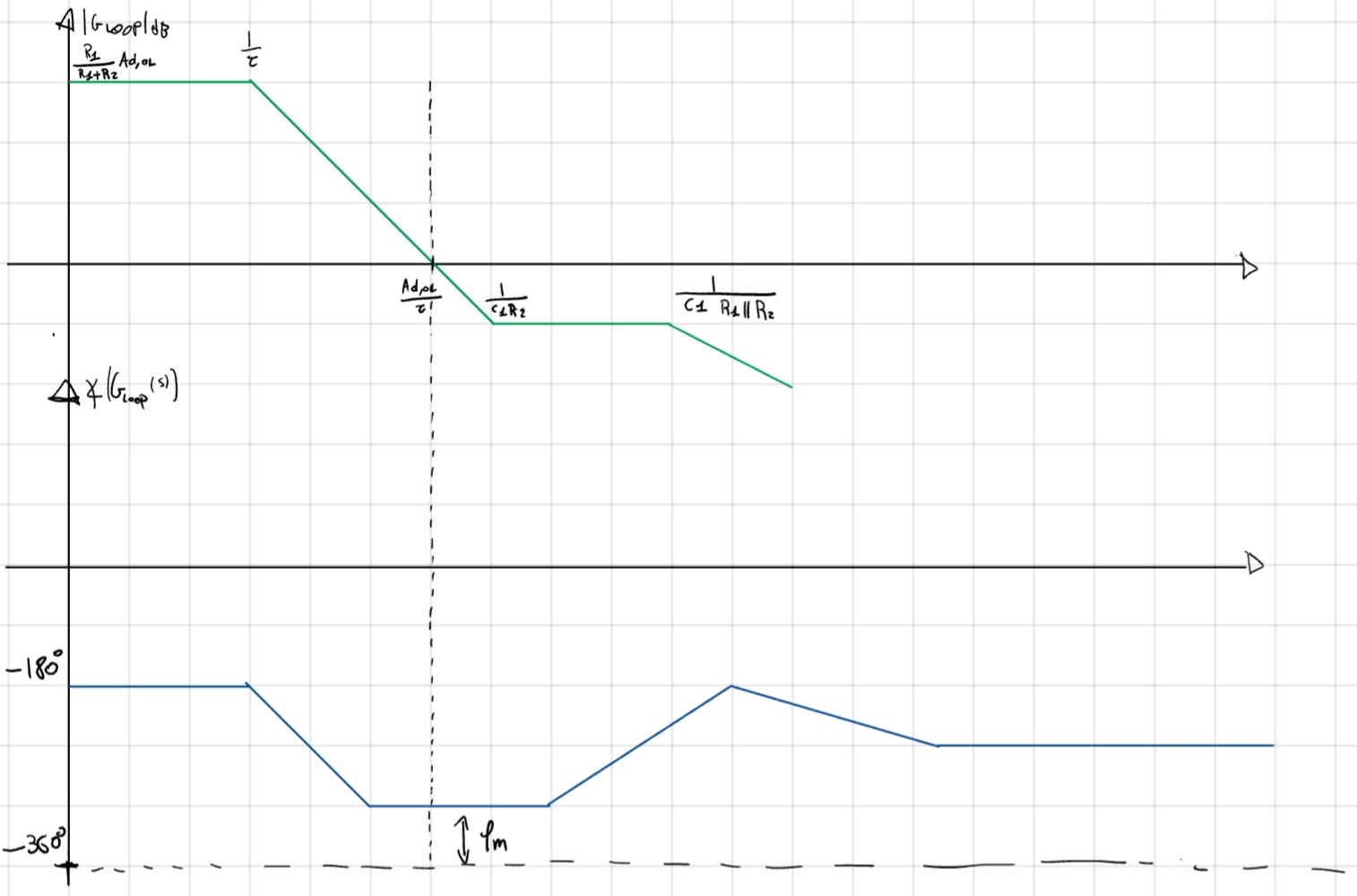
Ora cose che in FdA si sono già fatte in maniera più dettagliata ma in sostanza si osserva che, quando |G_{LOOP}(f)|_{dB} = 0dB:
- Se taglia a -60dB/dec \to sicuramente instabile.
- Se a -20dB/dec \to sicuramente stabile.
- in altri casi controllare per stare tranquilli.
Capitolo Dieci: Acquisizione Digitale (The End)
Come avviene l’acquisizione digitale ?
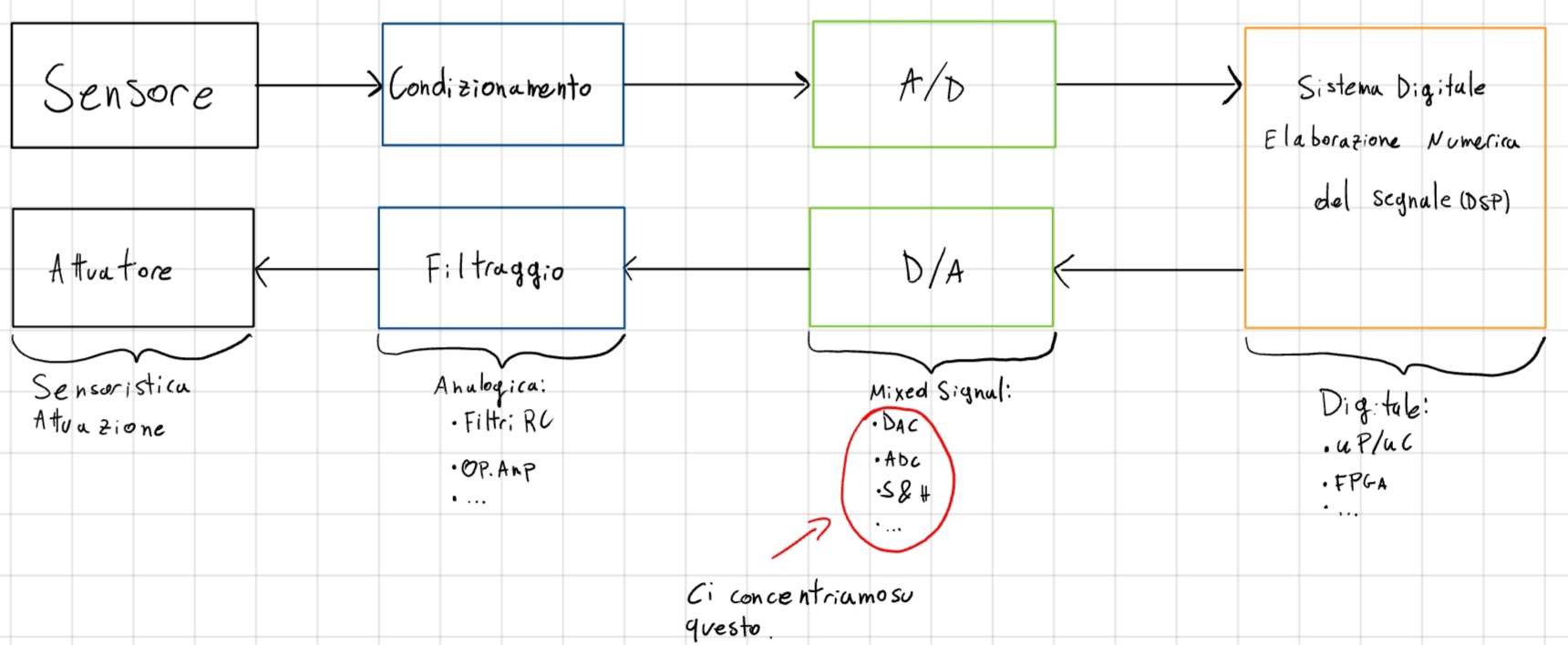
10.1 Digital - to - Amplitude Converter (DAC)
Trasforma un numero digitale (d) in una ampiezza analogica (V) compresa tra due valori: V_{DD} ed V_{SS}:
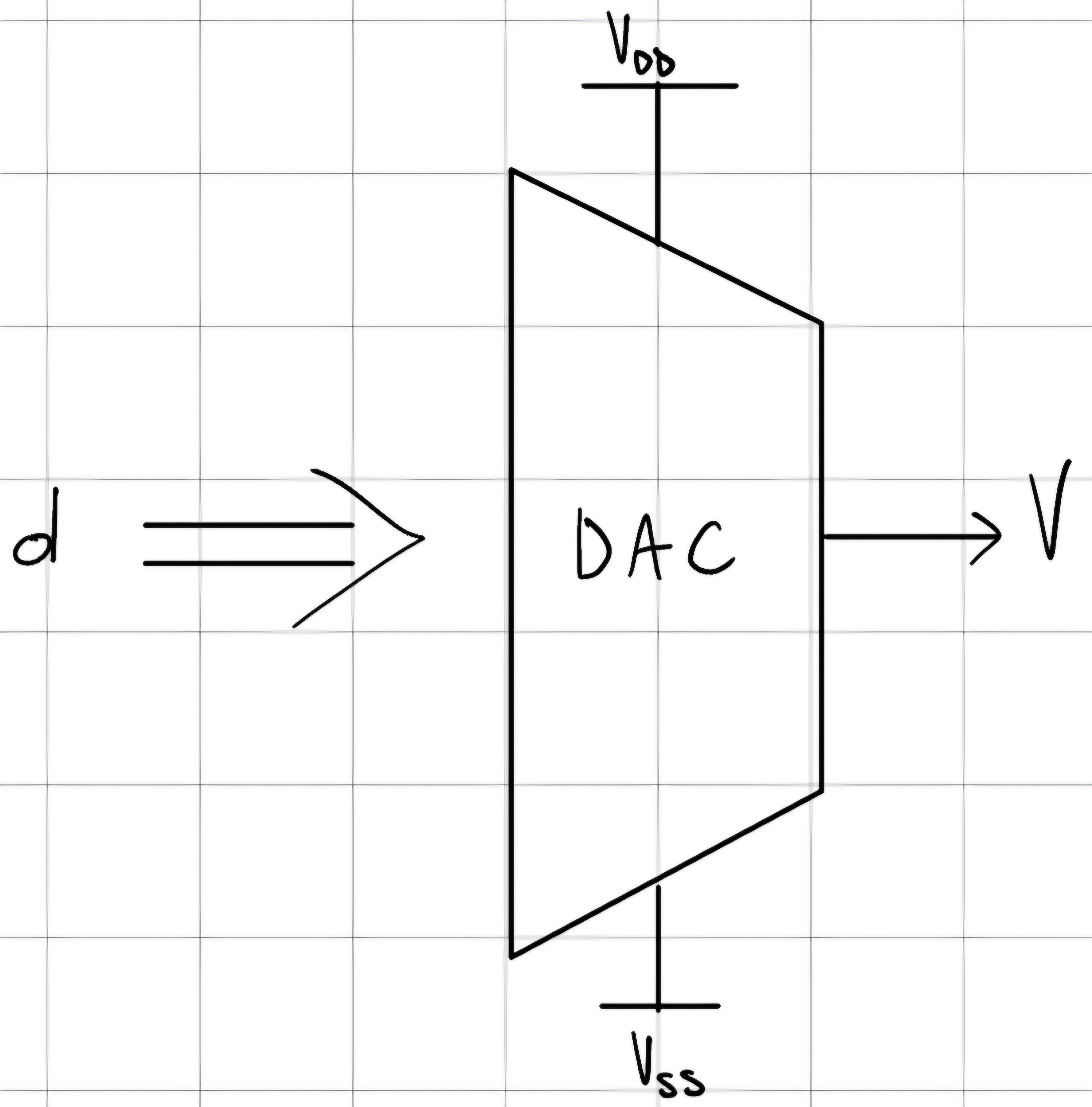
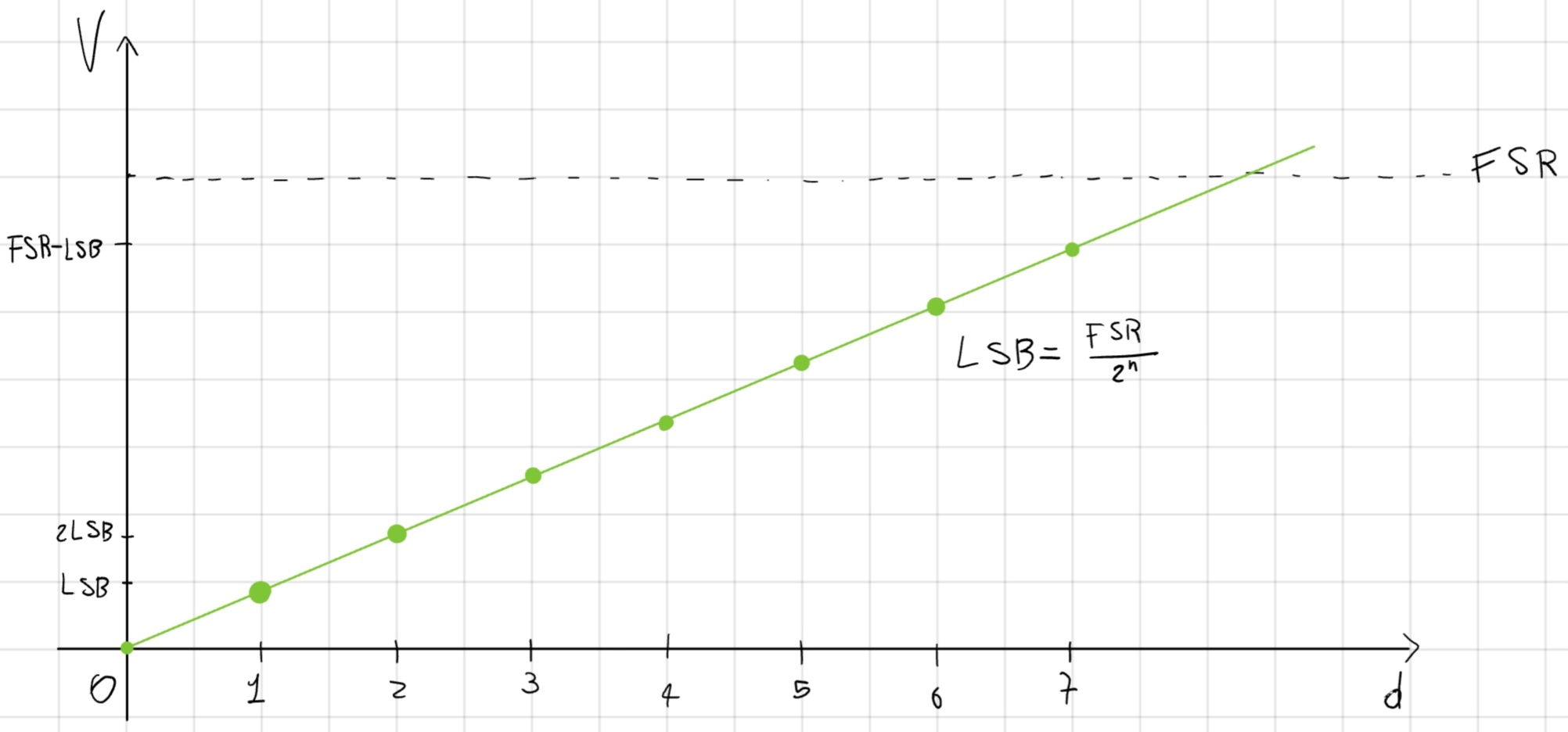
LSB = \frac{FSR}{2^n} \\ V = d \cdot LSB \\ d \in [0,2^n - 1] \\ FSR = V_{DD} - V_{SS} \\ n: \# bit
FSR = Full Scale Range.
LSB = Last Significant Bit o Risoluzione.
Errori
Offset, traslazione rispetto alla caratteristica ideale.
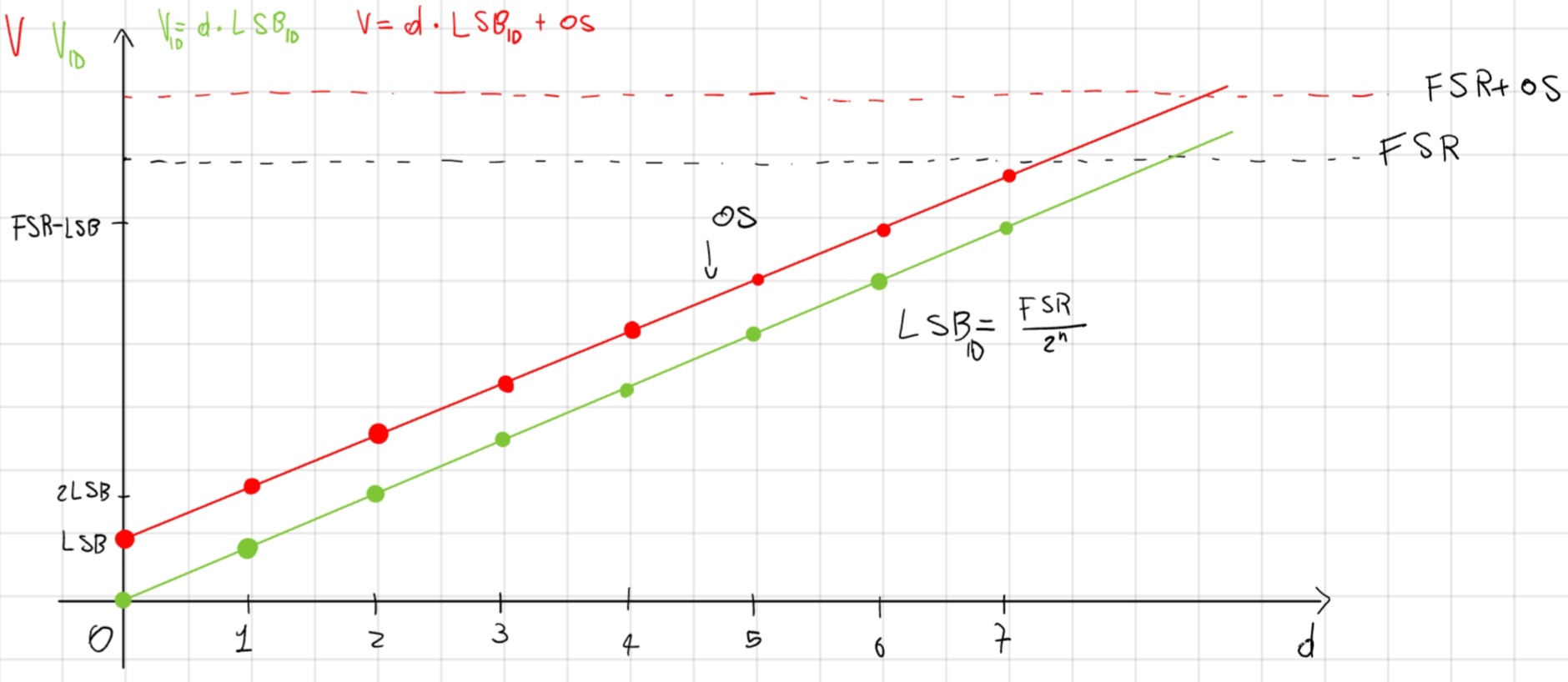
Guadagno, maggiore o minore pendenza rispetto alla caratteristica ideale.
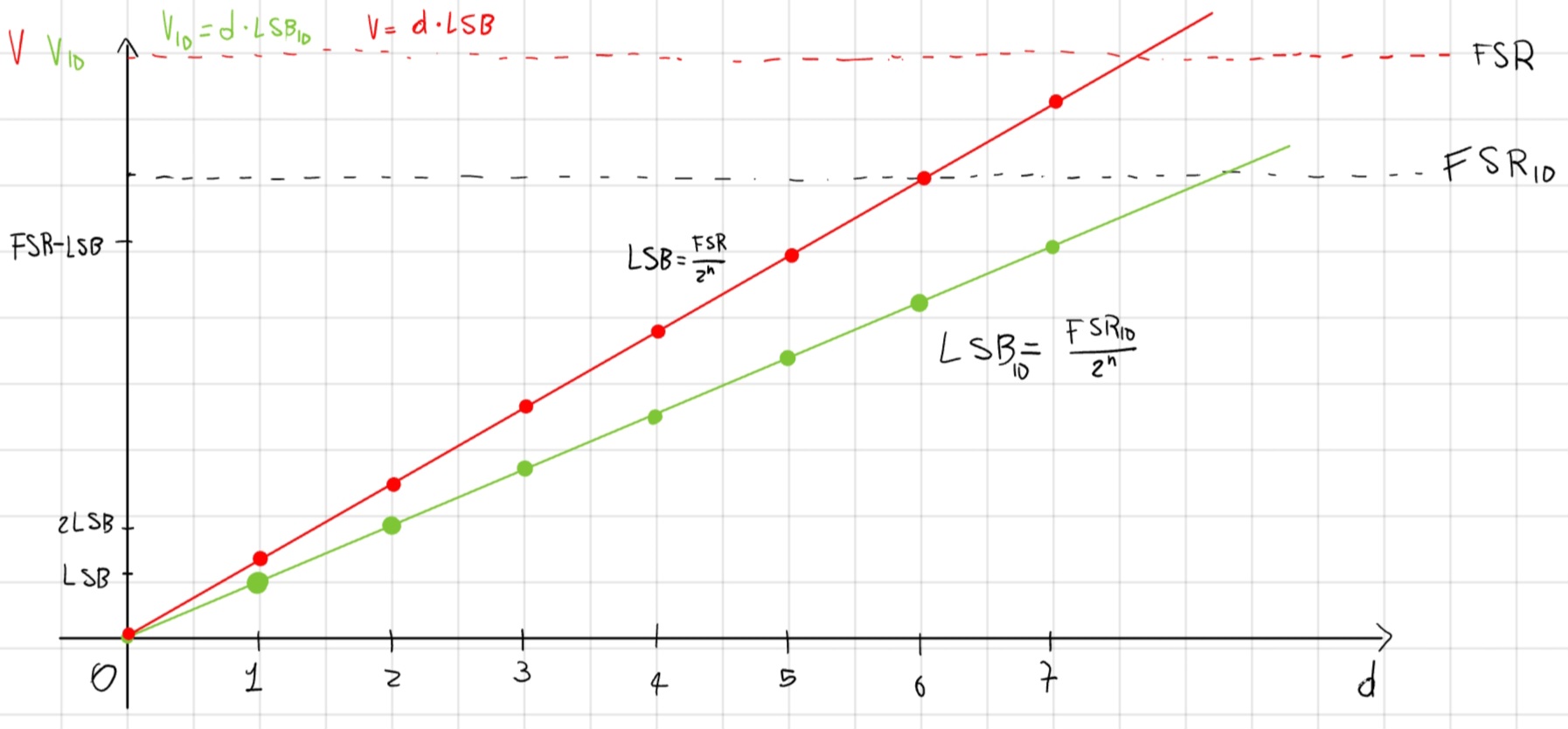
Non linearità, l’ampiezza degli intervalli cambia da codice a codice.
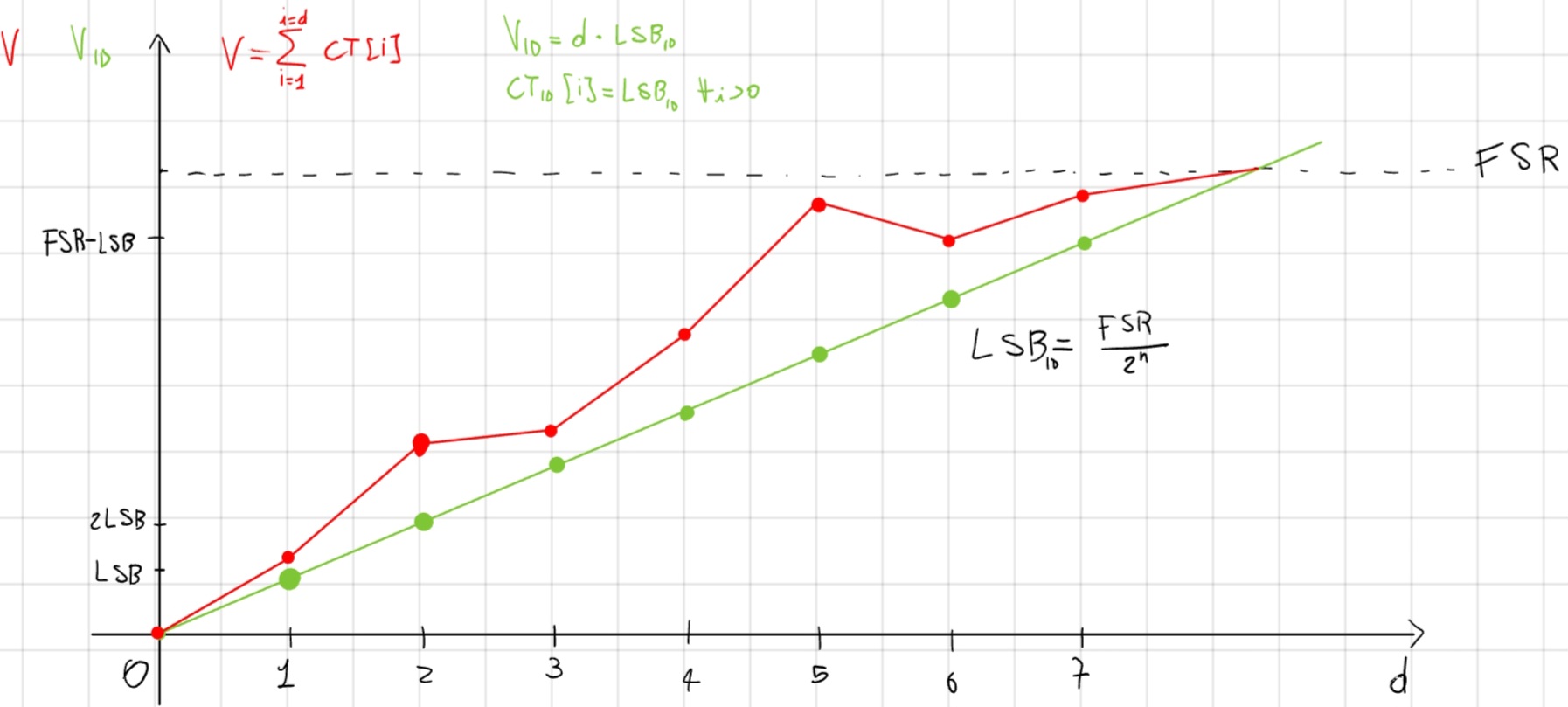
Non Linearità Differenziale (DNL)
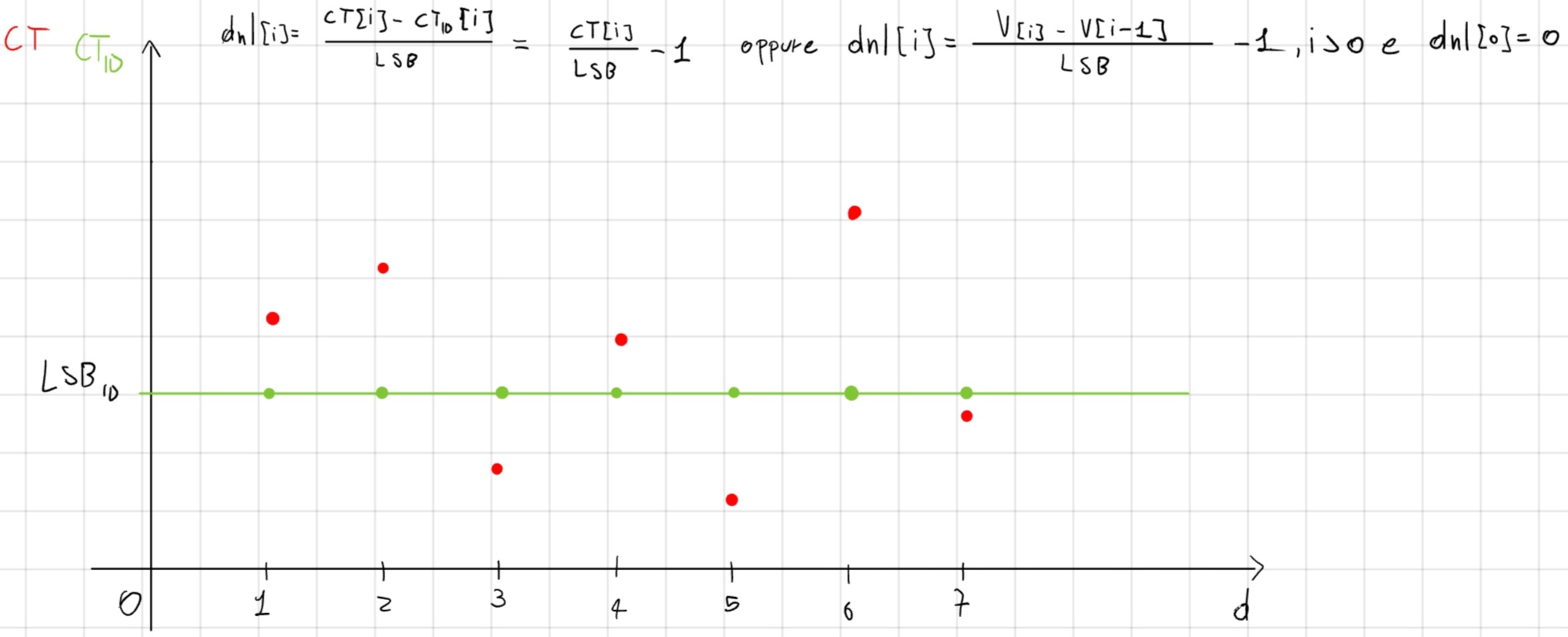
Non Linearità Differenziale Integrale (INL)
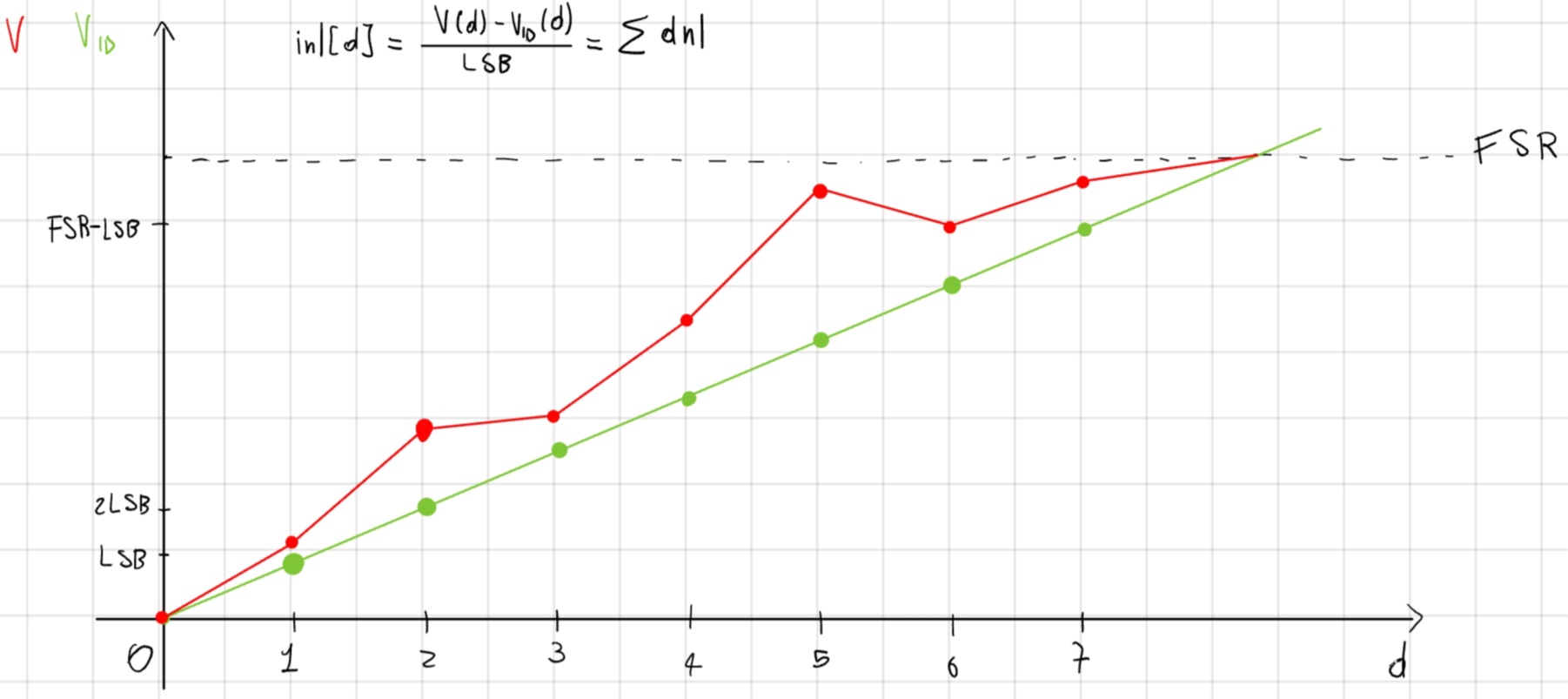
Setting-time, tempo necessario affinchè il livello di uscita V raggiunga il valore d \cdot LSB.
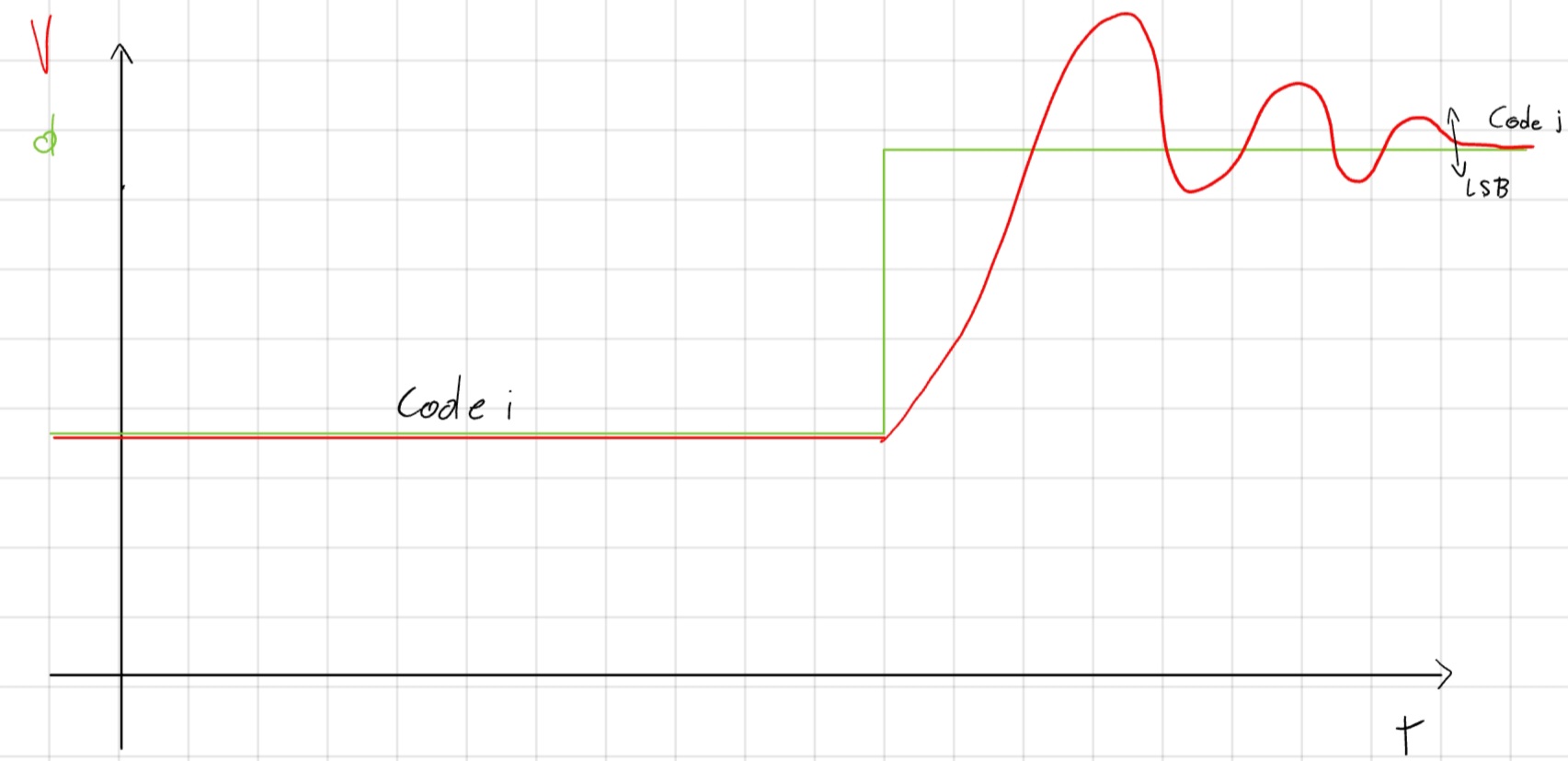
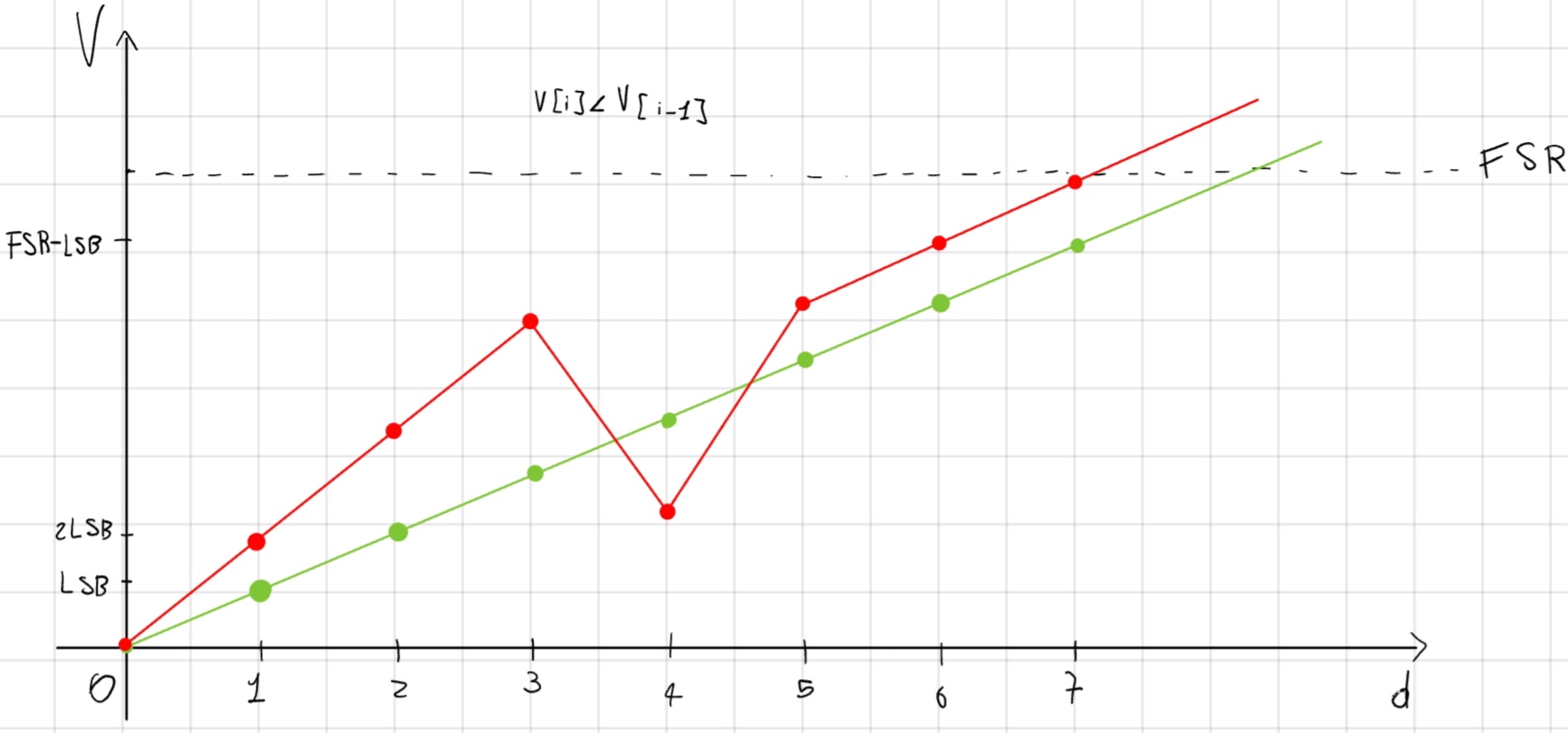
Non-monotocità, presenza di tratti di curva a pendenza negativa.
Struttura del DAC
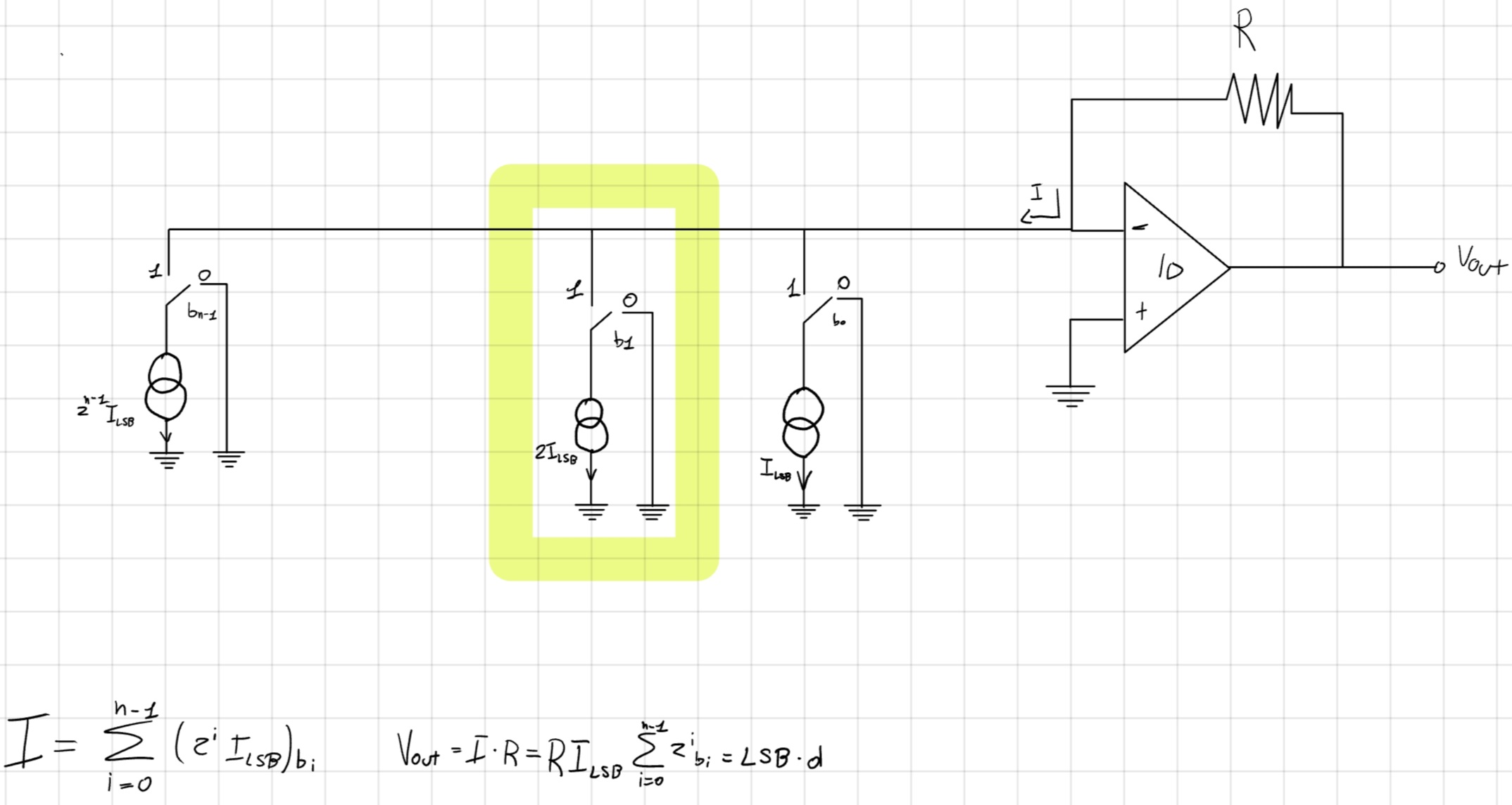
Cosa succede nei casi di NON-Idealità ?
- V_{OS} ed I_B^\pm, creano una V_{out} non nulla a fronte di un ingresso digitale d nullo, ovvero un errore di offset.
- A_0, genera un guadagno reale inferiore a quello R.
- GBWP, introduce poli/zeri della FdT \implies setting time.
- R_{parassita} switch \implies non linearità.
- Mismatch correnti pesate \implies anche qui non linearità.
10.2 Analog - to - Digital Converter (ADC)
Trasforma una ampiezza analogica (V) compresa tra V_{DD} e V_{SS} in un valore numerico (d).
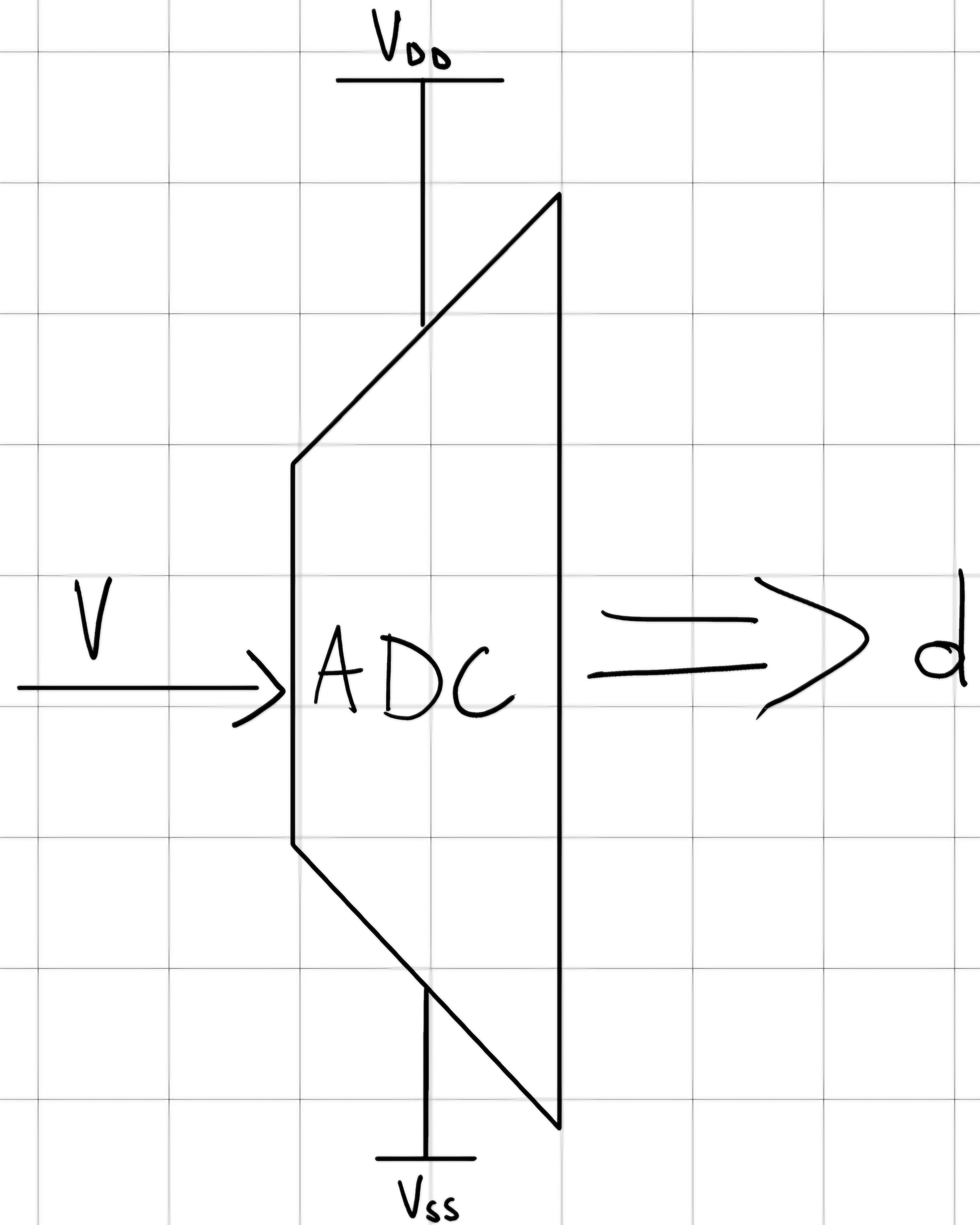
FSR = V_{DD} - V_{SS} \\ LSB = \frac{FSR}{2^n} \\ d = \frac{V}{LSB} \\ d \in [0, 2^n - 1] \subset \N \\ V \in [V_{SS}; V_{DD}] \equiv FSR - LSB
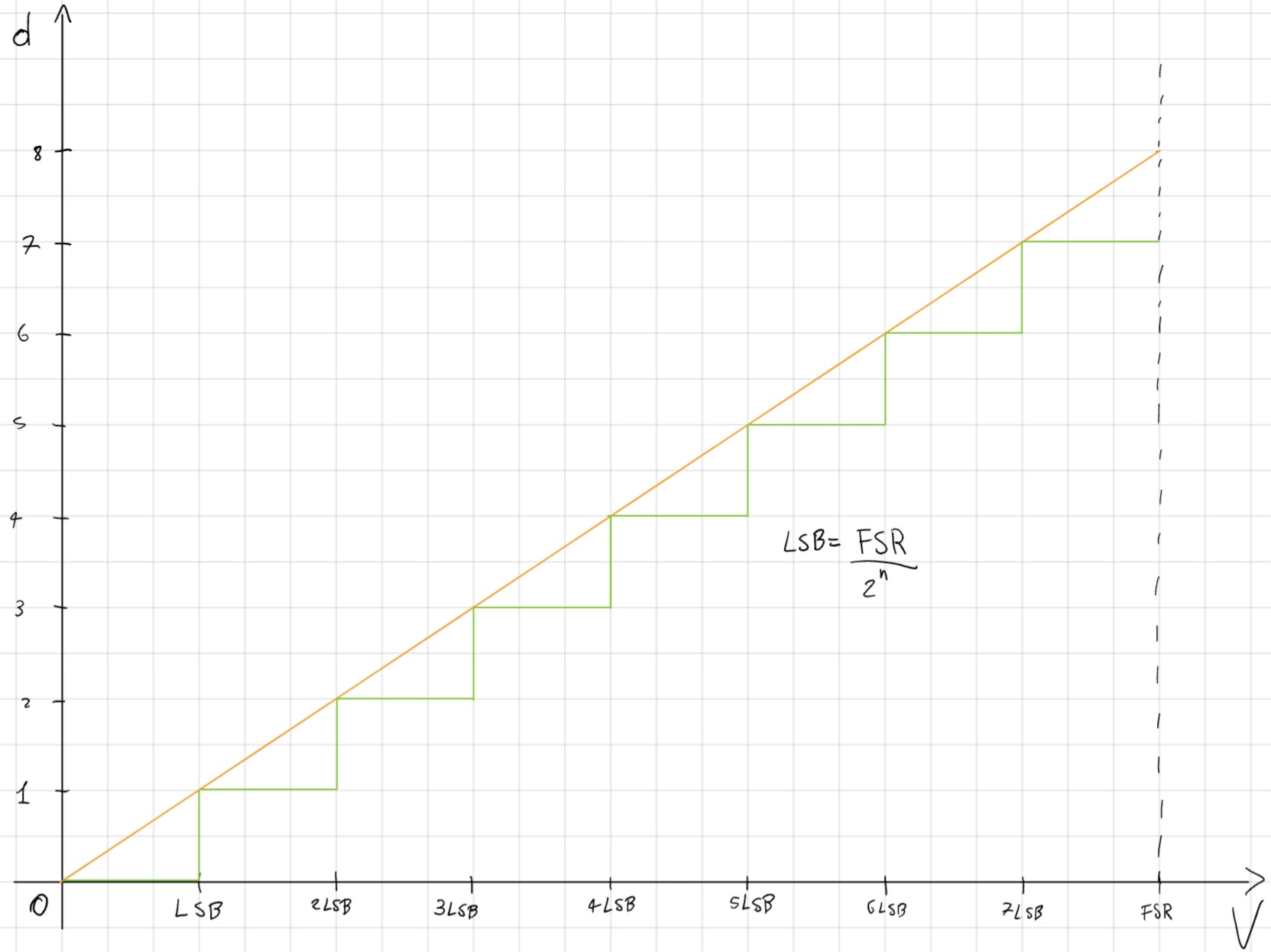
Errori
Quantizzazione, scostamento dovuto al troncamento/arrotondamento di V/LSB.
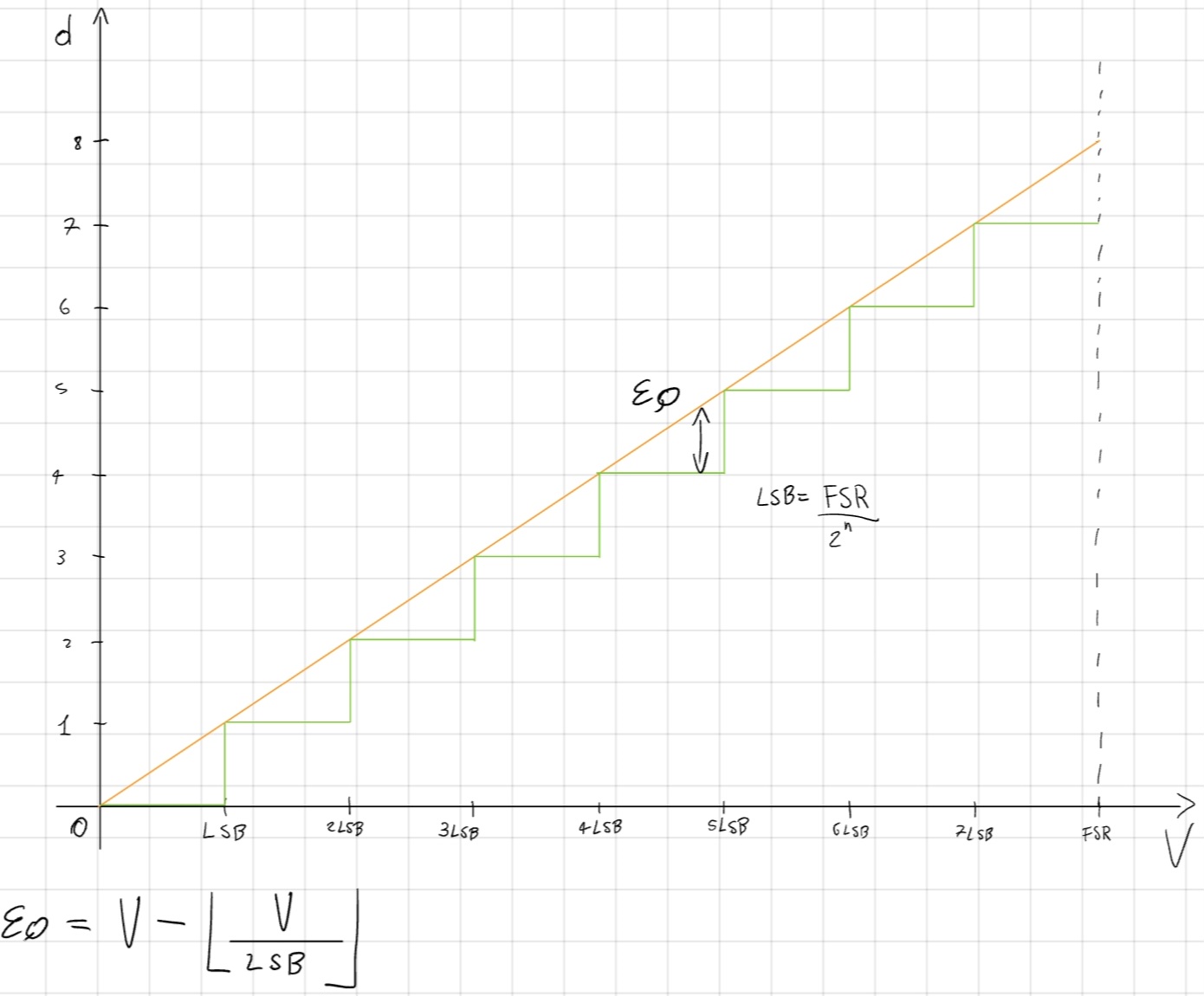
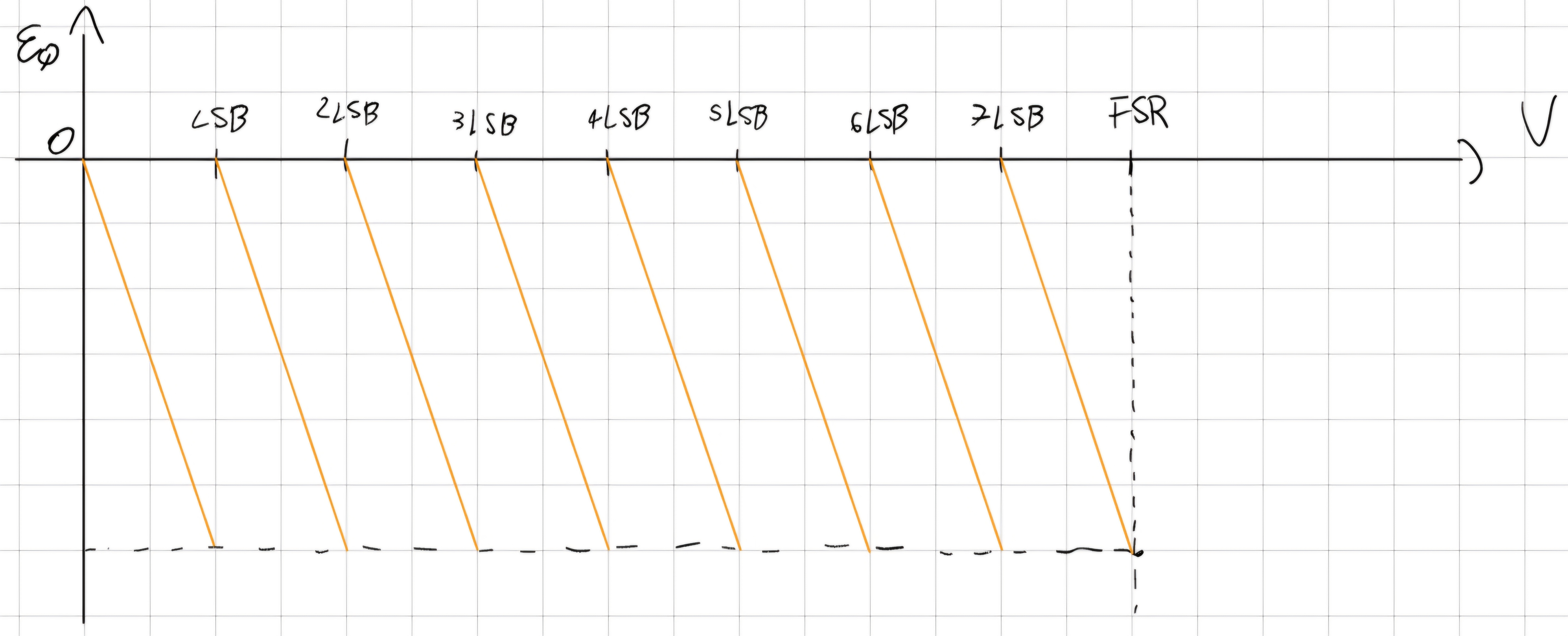
\overline{\varepsilon_Q} = \frac{1}{LSB} \int_{0}^{LSB} \varepsilon_Q(V) dV = \frac{1}{LSB} \int_{0}^{LSB} - VdV = -\frac{1}{LSB}\frac{V^2}{2}|_{0}^{LSB} = -\frac{LSB}{2}
\varepsilon_{Qeff}^2 = \frac{1}{LSB} \int_{0}^{LSB} \varepsilon_Q^2(V) dV = \frac{1}{LSB} \int_{0}^{LSB}(-V)^2 dV = \frac{1}{LSB} \frac{V^3}{3}|_0^{LSB} = \frac{LSB^2}{3}
\sigma_Q^2 = \frac{1}{LSB} \int_{0}^{LSB} [\varepsilon_Q (V) - \varepsilon_Q]^2 dV = \frac{LSB^2}{3} - (- \frac{LSB}{2})^2 = \frac{LSB^2}{12}
Offset, traslazione rispetto alla caratteristica ideale.
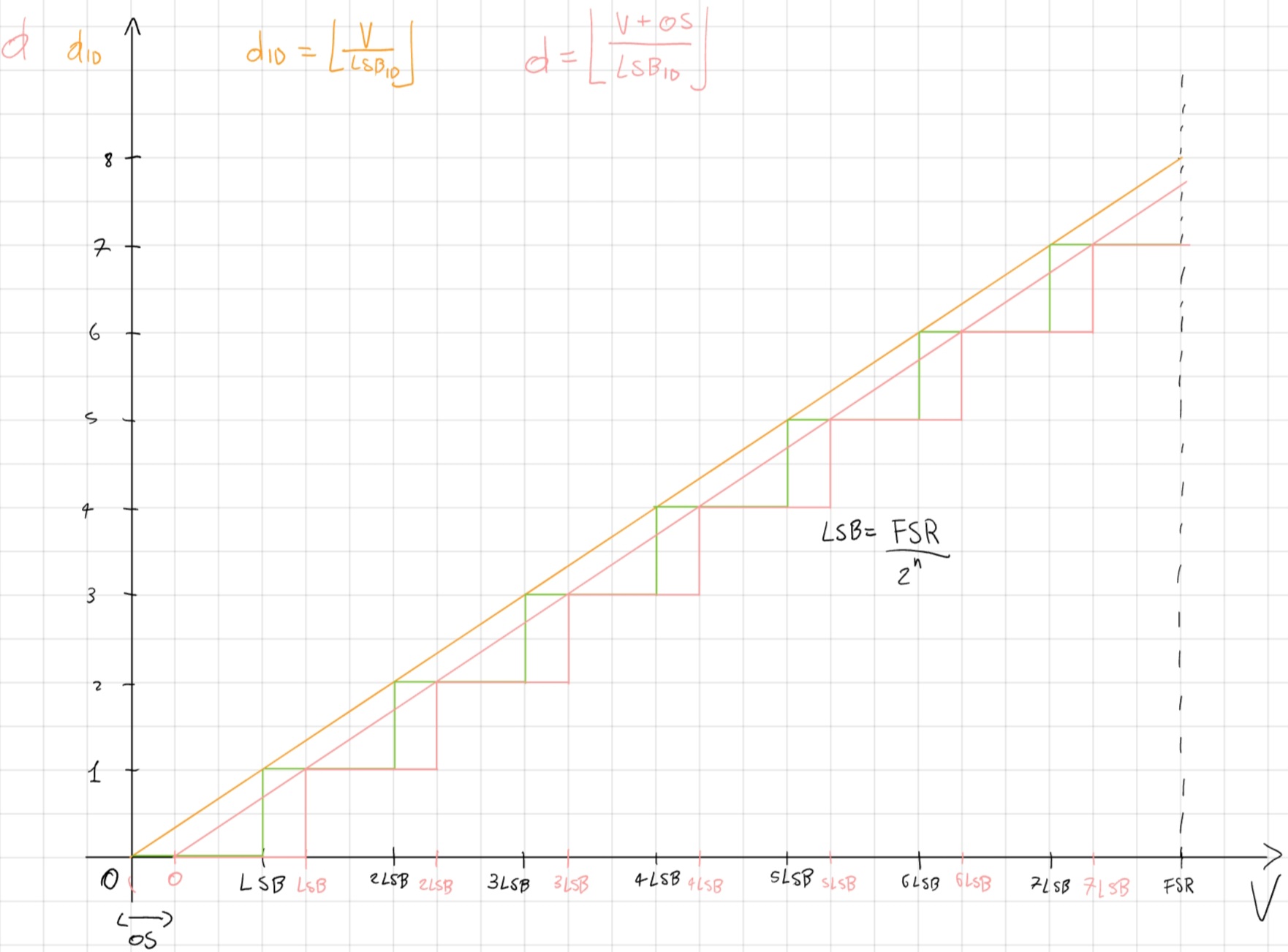
Guadagno, maggiore o minore pendenza rispetto alla caratteristica ideale.
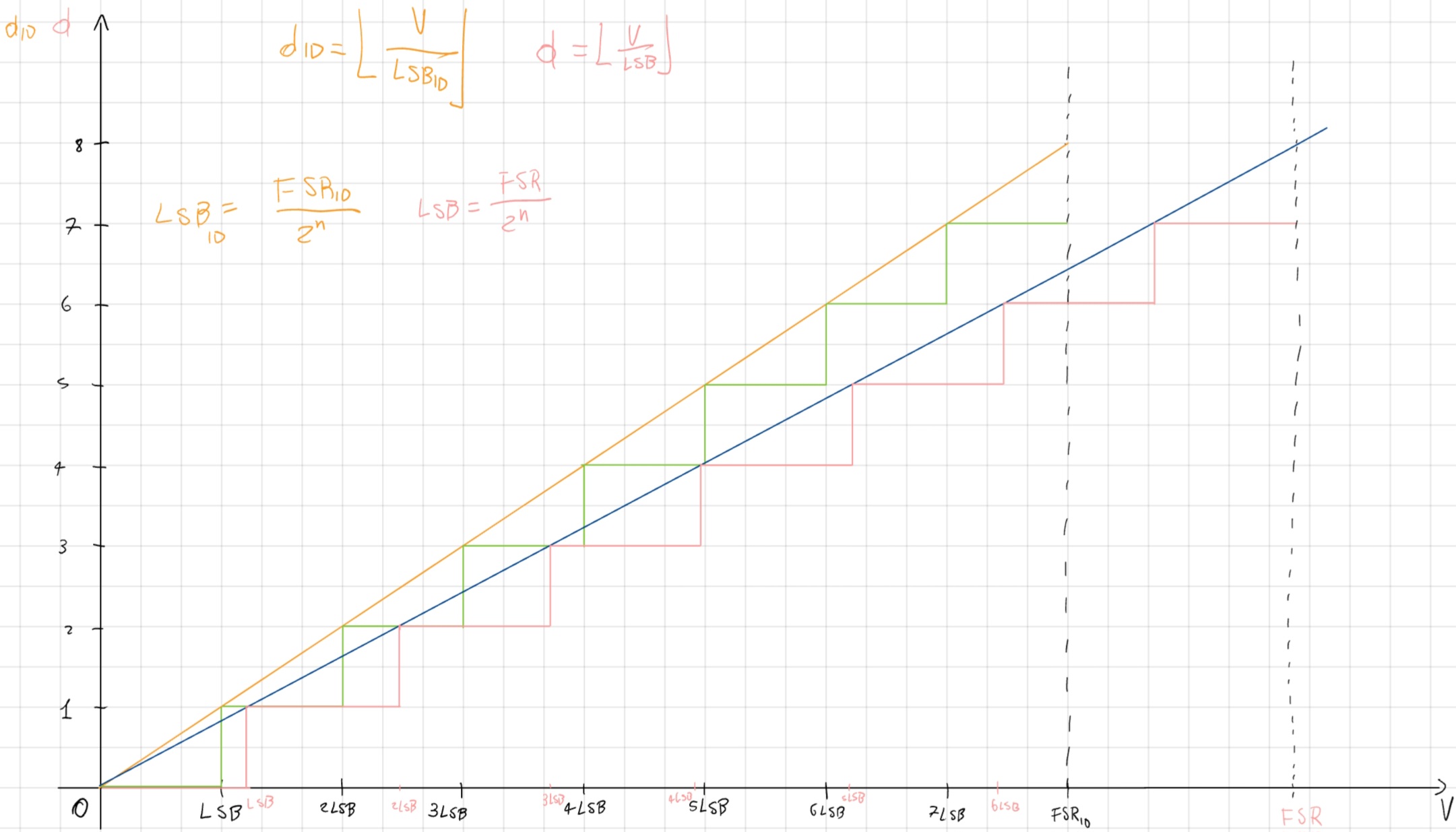
Non Linearità, l’ampiezza degli intervalli cambia da codice a codice.
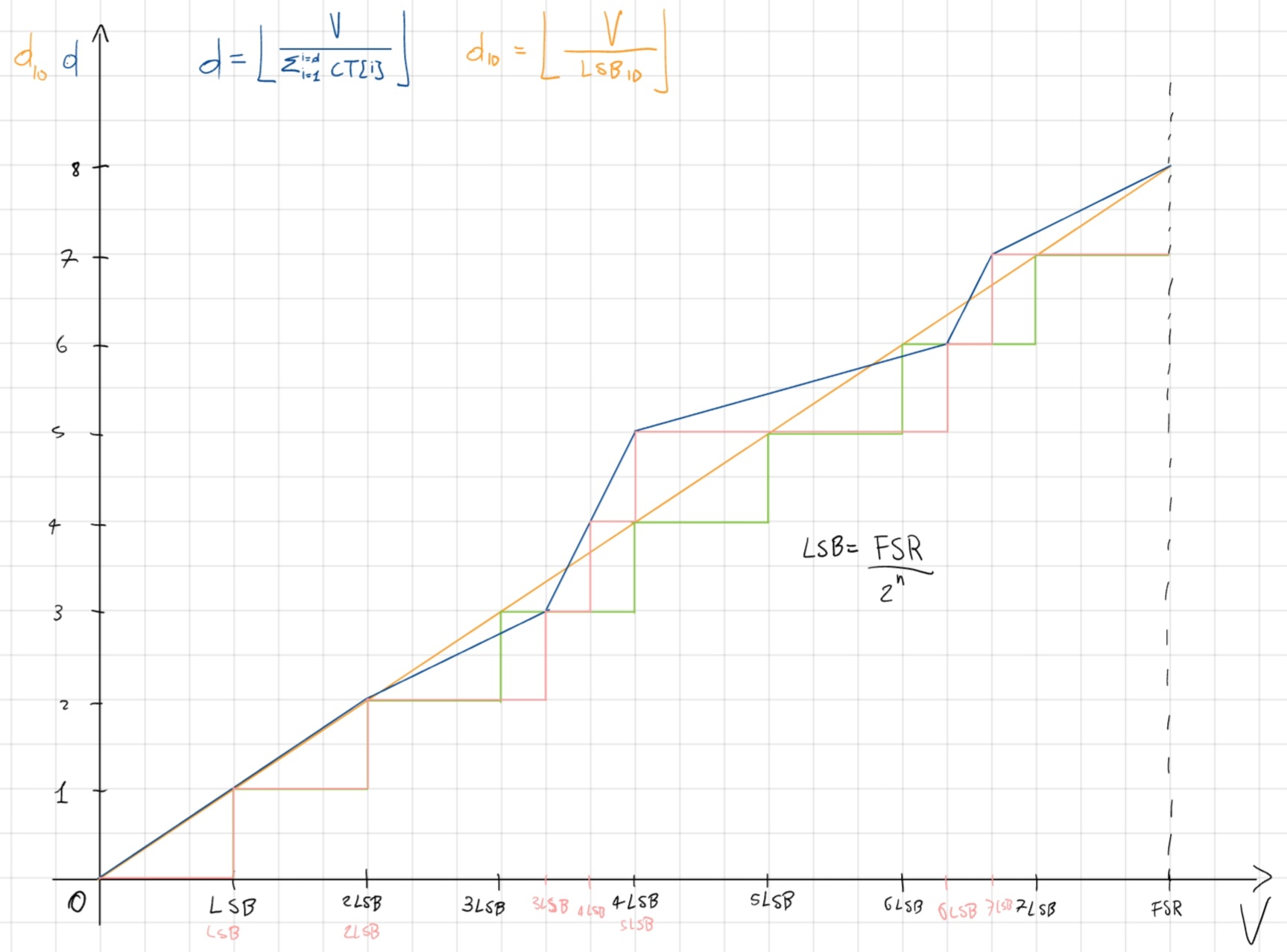
Non Linearità differenziale (DNL)
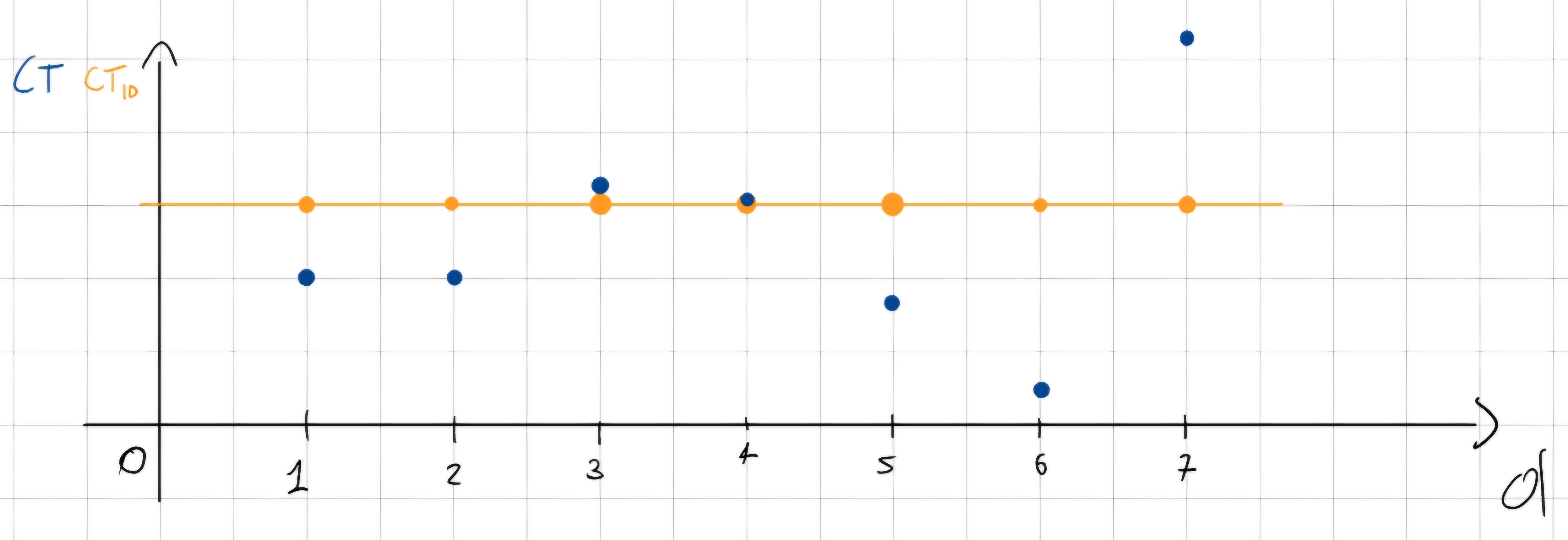
dnl[i] = \frac{CT[i] - CT_{ID}[i]}{LSB} = \frac{CT[i]}{LSB} - 1
oppure
dnl[i] = \frac{V[i] - V[i-1]}{LSB} - 1, i>0 e dnl[0] = 0
Non Linearità differenziale integrale (INL)
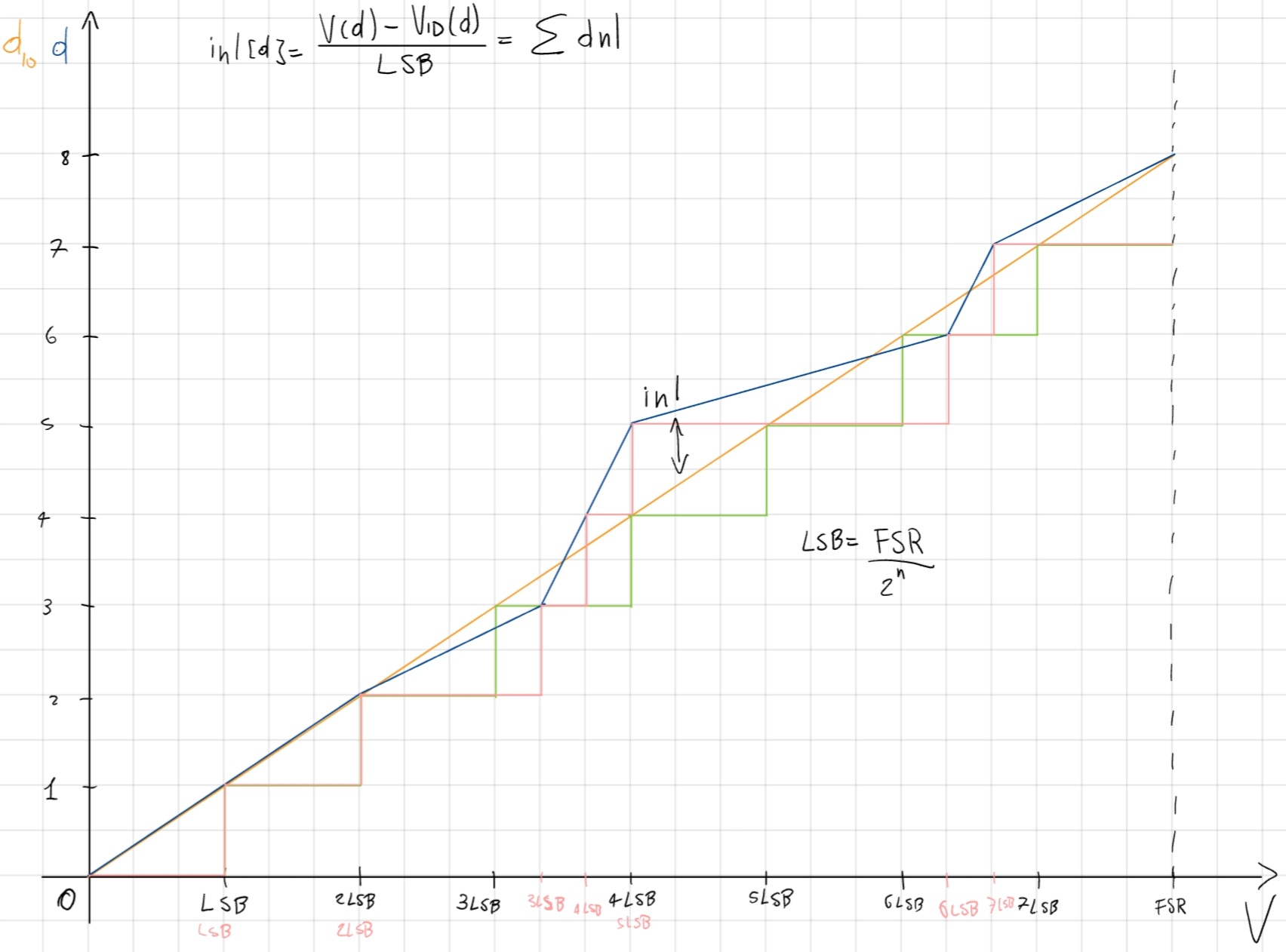
Conversione, tempo necessario affinchè venga prodotto il codice d’sucita avviando la conversione sul livello d’ingresso V.
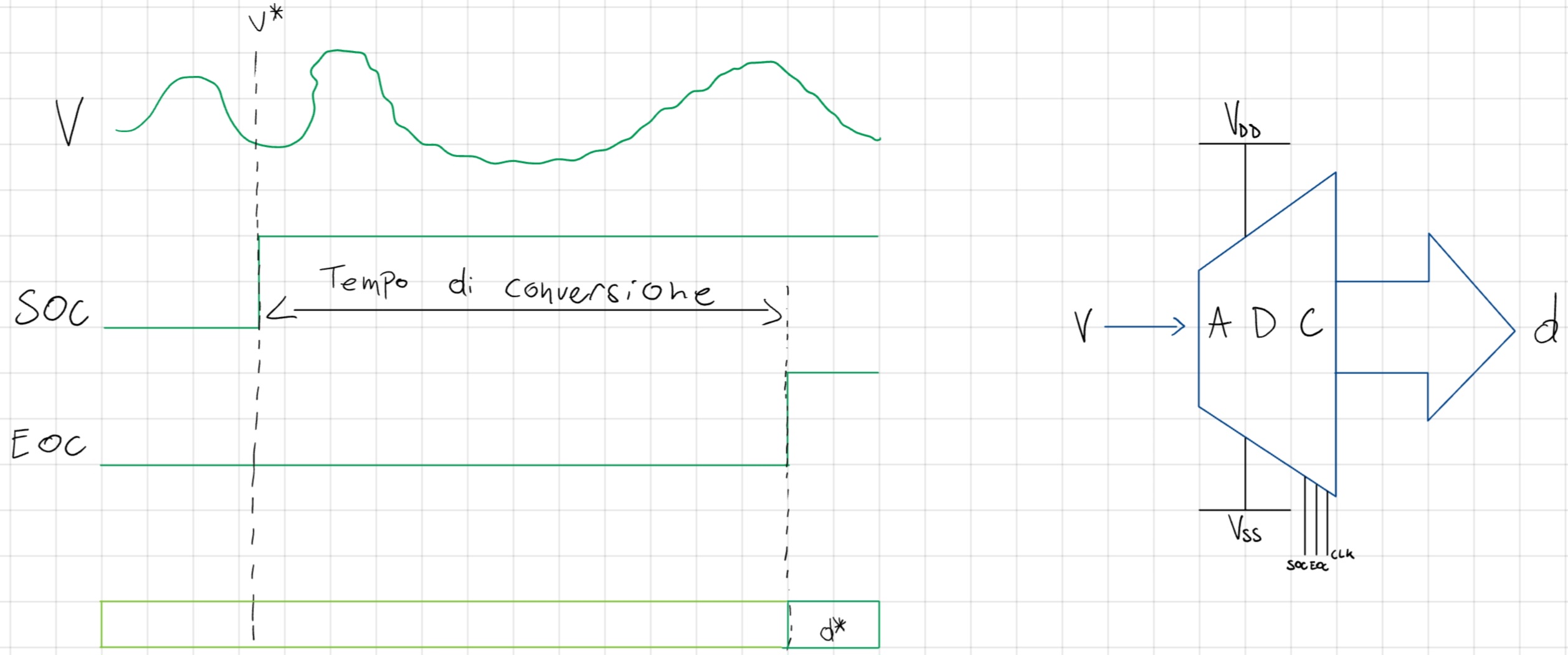
Codice mancante, alcuni codici non sono prodotti, così la caratteristica reale non è monotona.
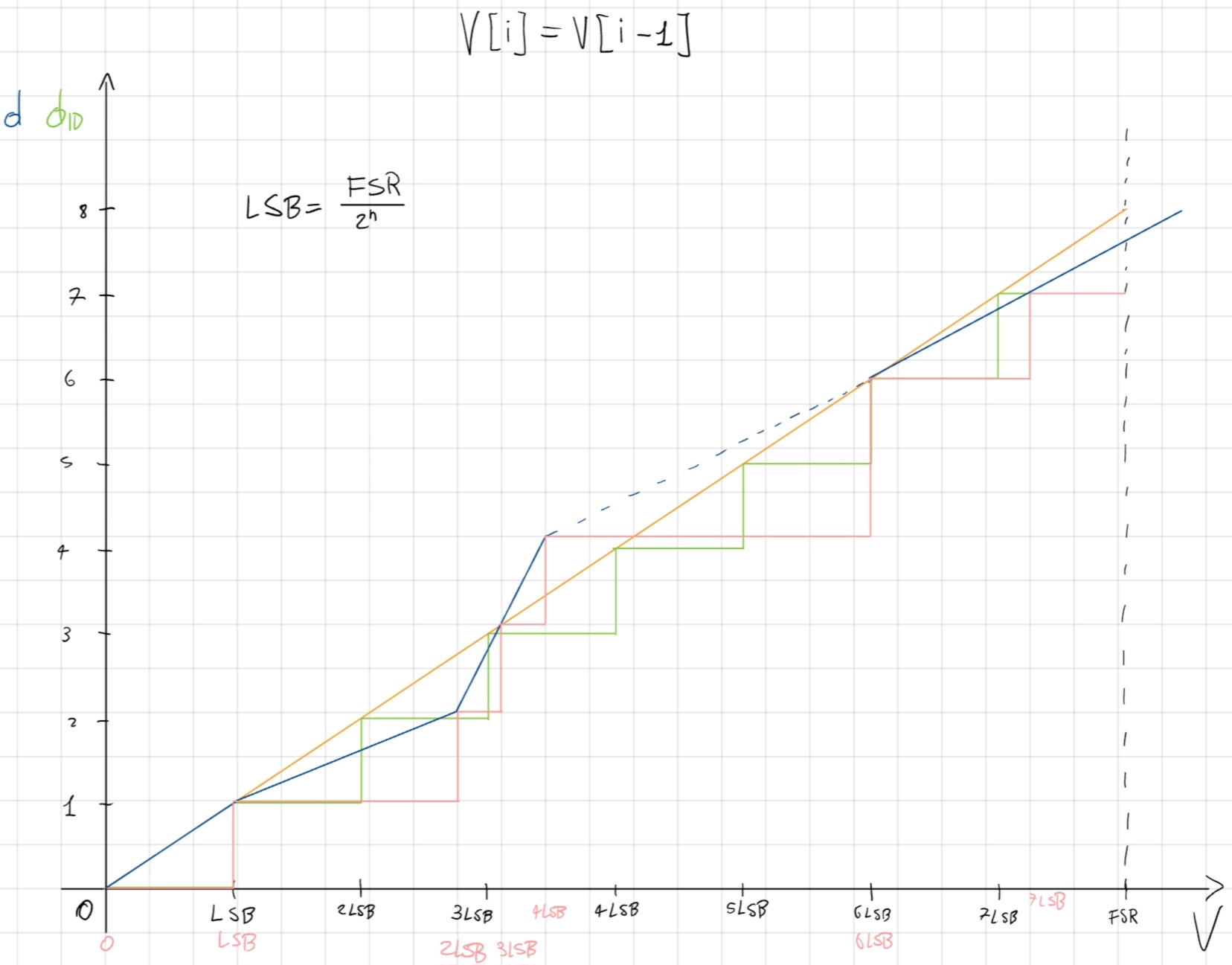
Massima pendenza d’ingresso
- Dobbiamo convertire il segnale V* in un tempo di conversione (T_{CONV}).
- Bisogna garantire che tra V(t_{SOC}) e V(t_{EOC}) ci sia uno scostamento minore di \plusmn \frac{LSB}{2}.
- In questo modo abbiamo una coerenza tra d* e V*.
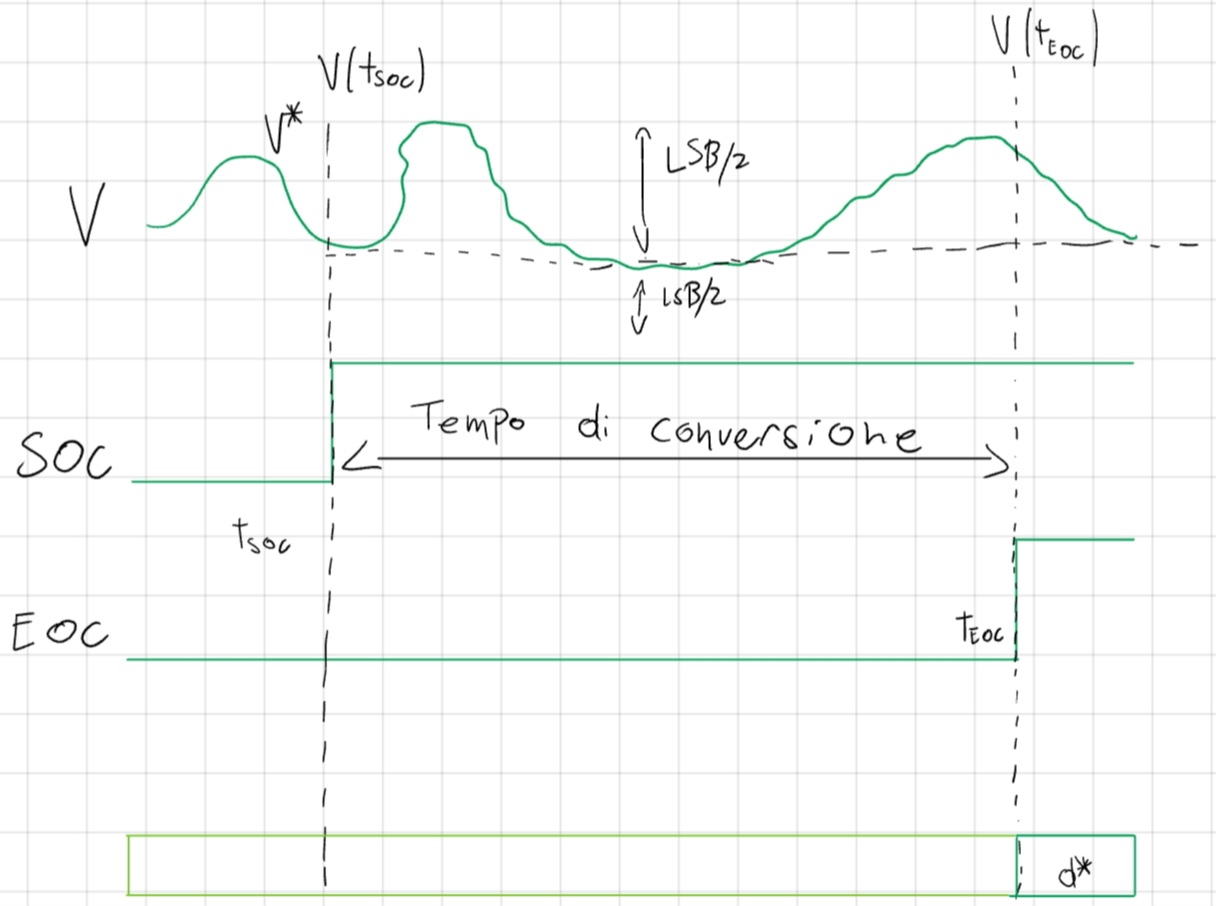
Da Fourier possiamo considerare solo la generica armonica i di ampiezza V_i e frequenza f_i:
V_i (t) = V_i sin(2 \pi f_i t)
\frac{d}{dt} V_i (t) |_{MAX} < \frac{\plusmn \frac{LSB}{2}}{T_{CONV|min}} \\ \frac{d}{dt} V_i sin(2 \pi f_i t)|_{MAX} T_{CONV} |_{min} < \plusmn \frac{LSB}{2} \\ 2\pi f_i V_i cos(2\pi f_i t)|_{MAX} T_{CONV}|_{min} < \plusmn \frac{LSB}{2} \\ cos(2 \pi f_i t) |_{MAX} = \plusmn 1 \\ V_i|_{MAX} = \plusmn \frac{FSR}{2} \\ 2 \pi f_i |_{MAX} V_i |_{MAX} cos(2 \pi f_i t) |_{MAX} T_{CONV}|_{min} < \plusmn \frac{LSB}{2} \\ 2 \pi f_i |_{MAX} \frac{FSR}{2} \plusmn 1 \cdot T_{CONV} |_{min} < \plusmn \frac{LSB}{2} \\ 2 \pi f_i |_{MAX} \frac{FSR}{2}T_{CONV}|_{min} <\frac{FSR}{2} \\ f_i |_{MAX} < \frac{1}{2 \pi}\frac{LSB}{FSR} \frac{1}{T_{CONV|min}} \\ f_i |_{MAX} < \frac{1}{2 \pi} \frac{1}{2^n} \frac{1}{T_{CONV|min}}
10.3 Tipi di ADC
ADC Flash
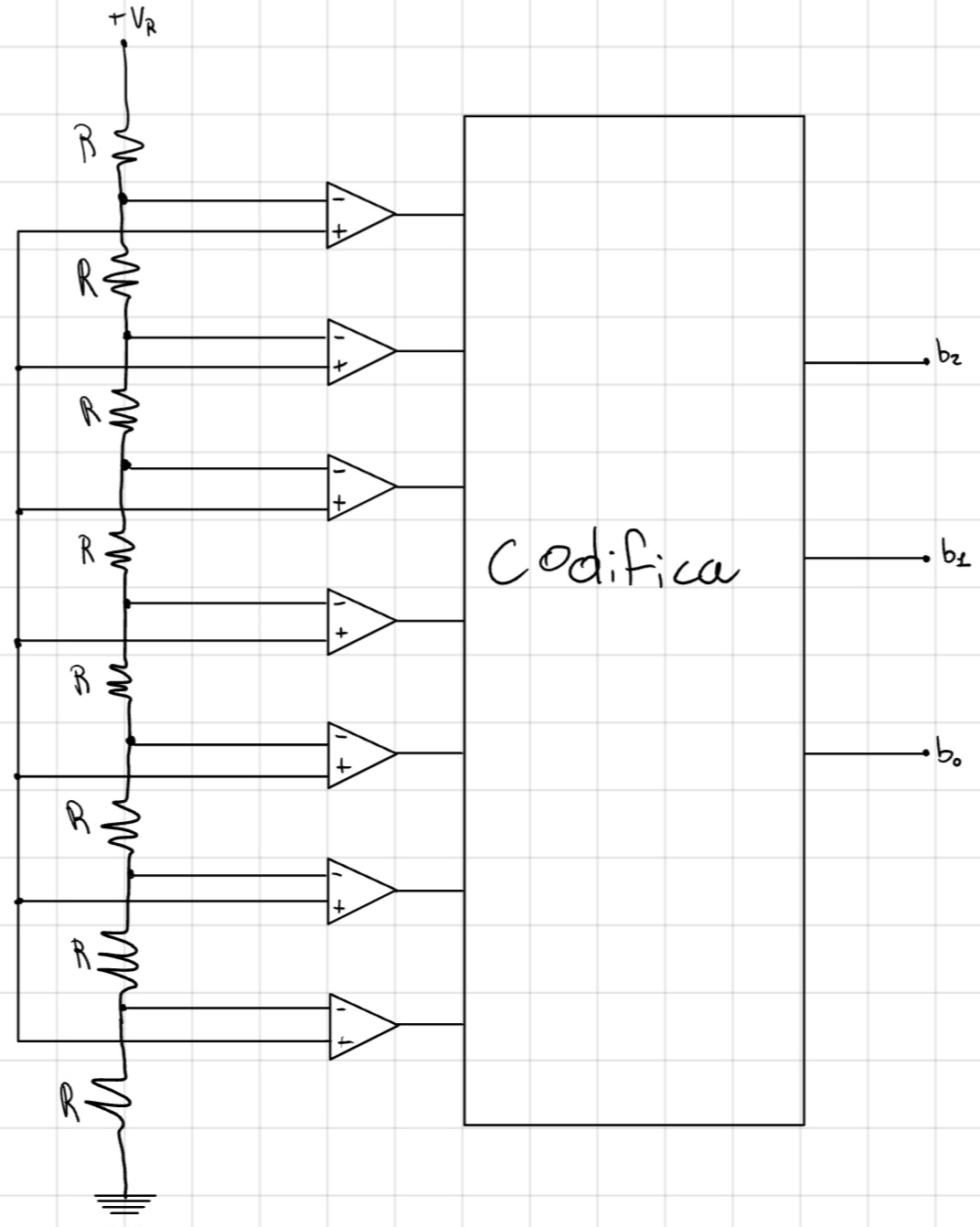
Molticomparatori (2^n - 1)
- Consuma tanta potenza.
- Matching difficile (DNL, INL).
Velocità Elevata
- T_{CONV} = T_{CLK}
Pochi bit (max 12) ad altissima velocità (GHz) e consumo di potenza.
ADC a Rampa Digitale
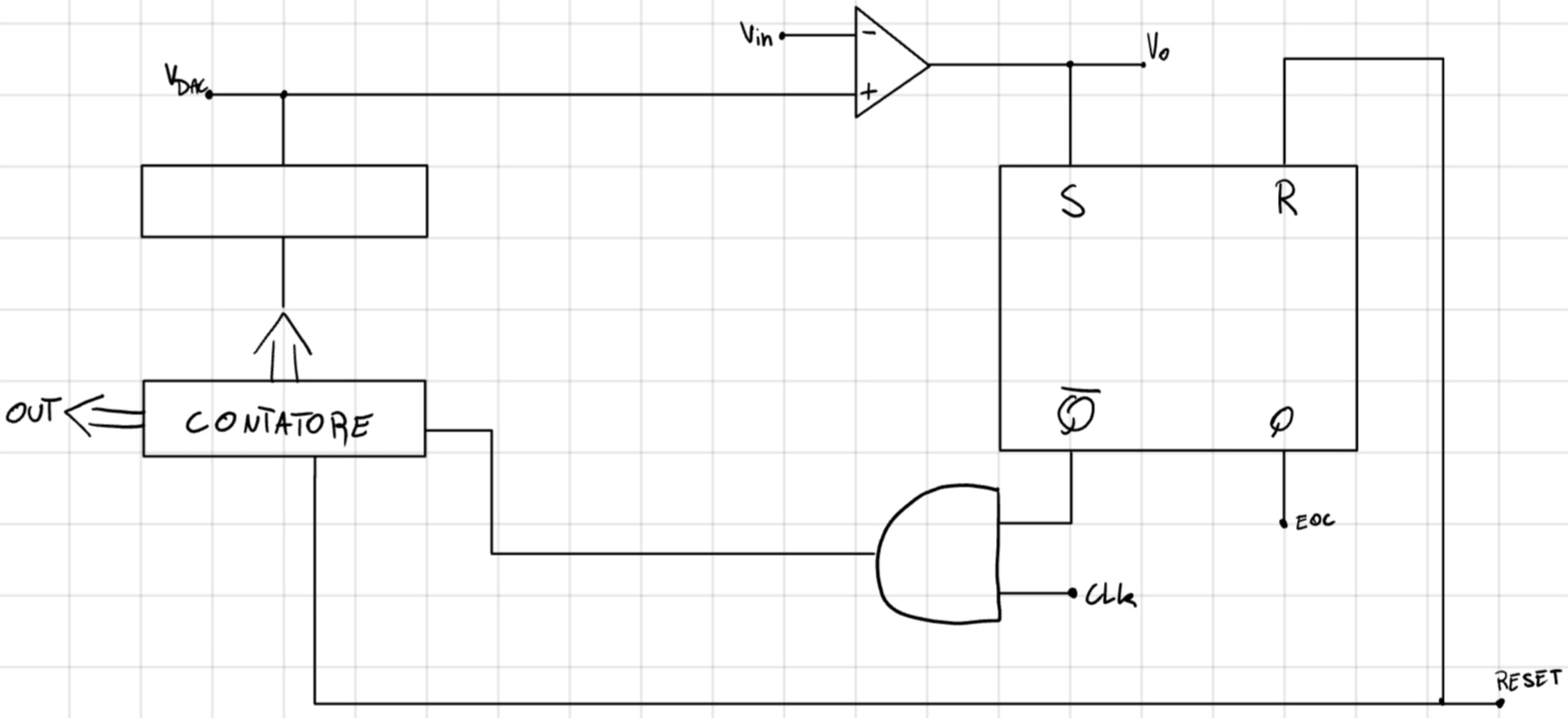
Semplice Logica
- Consumi bassi
- Usa molti bit
Tempo di conversione dipendente da V
- T_{CONV} \frac{FSR}{LSB}T_{CLK}
- T_{CONV|MAX} = 2^n T_{CLK}
DNL, INL, offset e Gain dipendenti solo dal DAC.
Contatore digitale da 0\text{X} 0...0 a 0 \text{X} F...F.
Un DAC coverte il conteggio in livello di tensione.
Un comparatore confronta il livello del DAC con quello in ingresso V.
L’uscita del comparatore ferma il conteggio ottenendo d.
ADC Tracking
- Funzionamento simile alla rampa digitale.
ADC a SAR
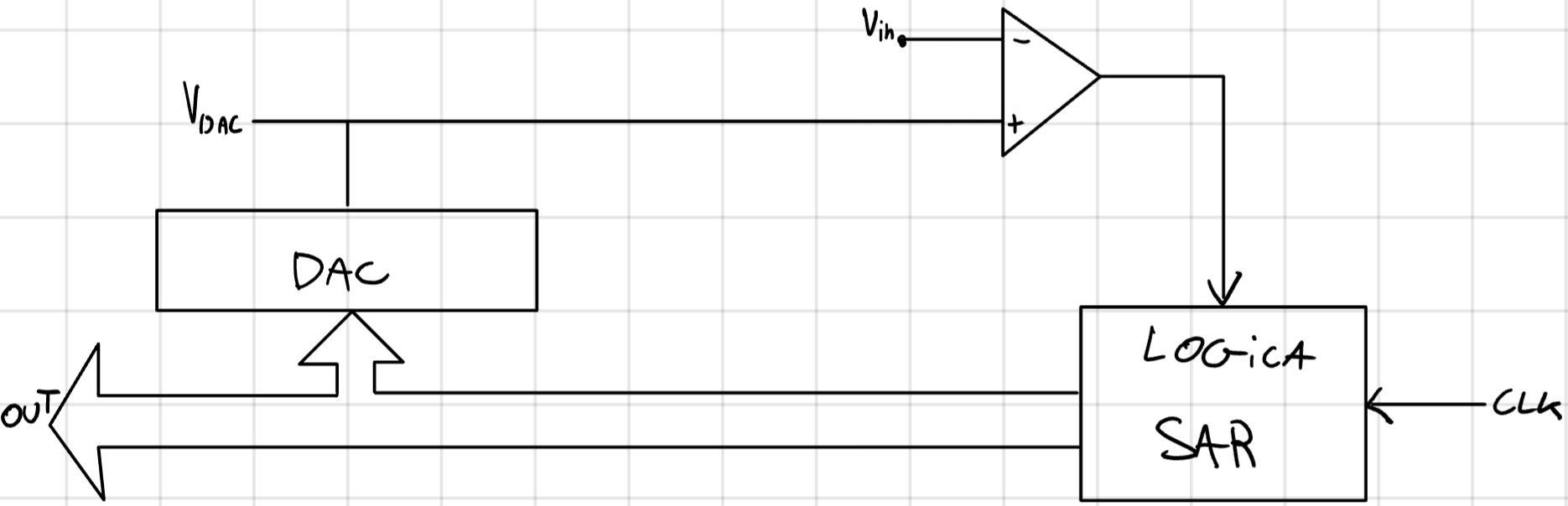
Logica SAR
Partiamo dal MSB di d,
- Se V_{in} > V_{dac} \to 1, else \to 0
Muoviamoci su MSB - 1 di d ricordandoci il valore di MSB,
- Se V_{in} > V_{dac} \to 1, else \to 0
Così fino ad LSB
- Se V_{in} > V_{dac} \to 1, else \to 0
Simile alla rampa digitale, il contatore è sostituito da una logica ad approssimazioni successive (SAR).
- In questo modo servono n colpi di clock per ogni livello di V.
- Consumi bassi.
- Usa molti bit.
- T_{CONV} = n \cdot T_{CLK}
- DNL, INL, offset e Gain dipendenti solo dal DAC.
ADC a Rampa
Come l’ADC a rampa digitale ma il contatore + DAC è sostituito da una rampa analogica.
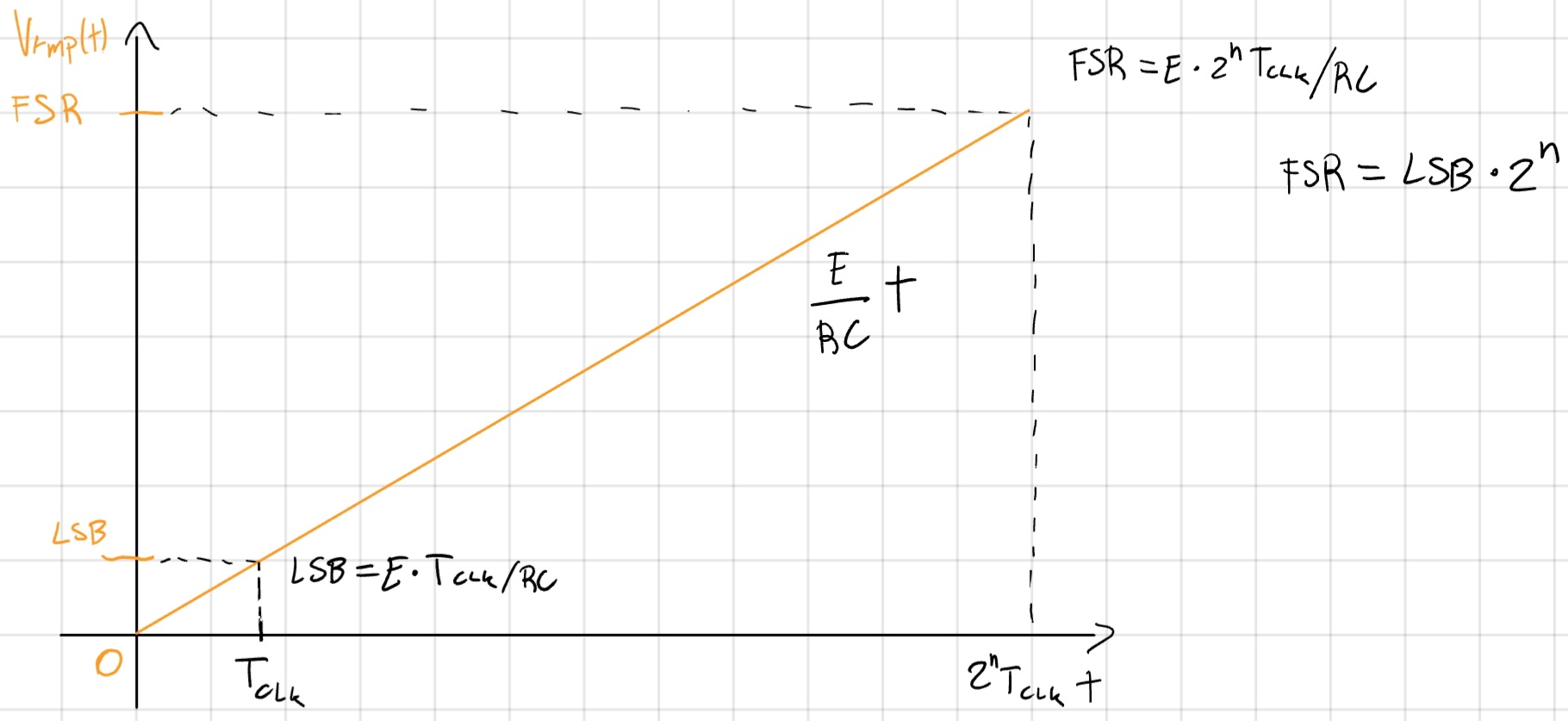
Un integratore ideale genera una rampa sul FSR:
- V_{rmp} (t) = \frac{E}{RC} t
Un clock alimenta un contatore che continua a contare.
Quando V_{rmp} (t) supera V:
- Si ferma il conteggio.
- Il valore del conteggio rappresenta d e viene posto in uscita.
- Viene resettata V_{rmp} (t) per una nuova conversione.
- Consumi bassi.
- Usa molti bit.
- T_{CONV} = \frac{V}{\frac{E}{RC}} = RC \cdot \frac{V}{E}.
- T_{CONV|MAX} = RC \frac{FSR}{E} = 2^nT_{CLK}
- DNL, INL, offset e Gain dipendono solo dall’OpAmp.
- I rumori/disturbi su E e V entrano 1:a:1 nella conversione A/D.
- FSR = E \cdot 2^nT_{CLK}/RC.
- LSB = E \cdot T_{CLK}/RC.
ADC a Doppia Rampa
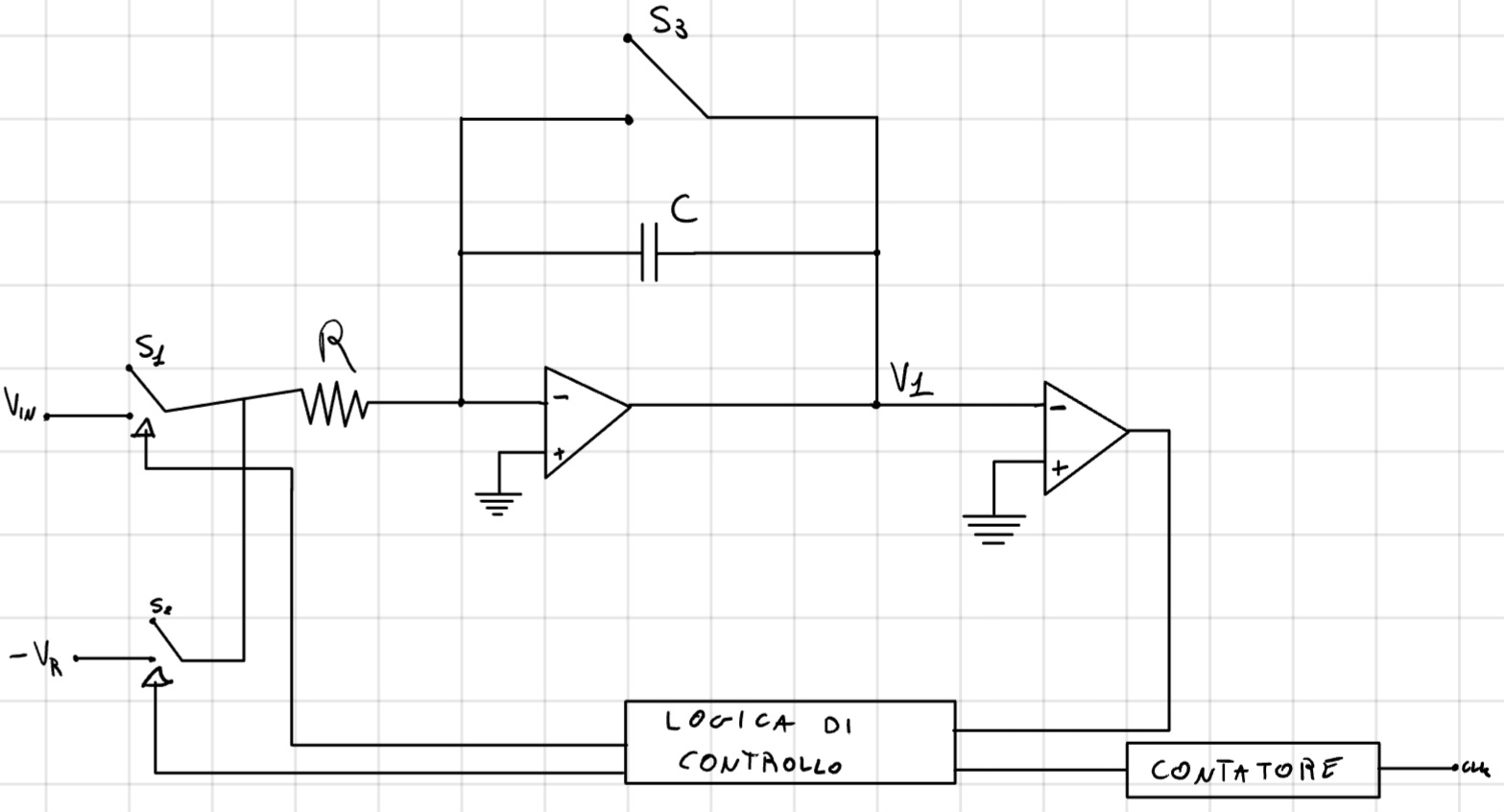
Simile alla rampa singola.
Carichiamo C(V_1) con V_{in} usando una rampa 1,T_1:
- V_{rmp,1}(t) = - \frac{V_{in}}{RC} t
- T_1 costante, scelto arbitrariamente.
- V_{rmp,1} (T_1) = - \frac{V_{in}}{RC}T_1.
Scarichiamo C(V_1) con la seconda rampa 2,T_2:
- V_{rmp,2}(t) = - \frac{-V_R}{RC} t = \frac{V_R}{RC} t.
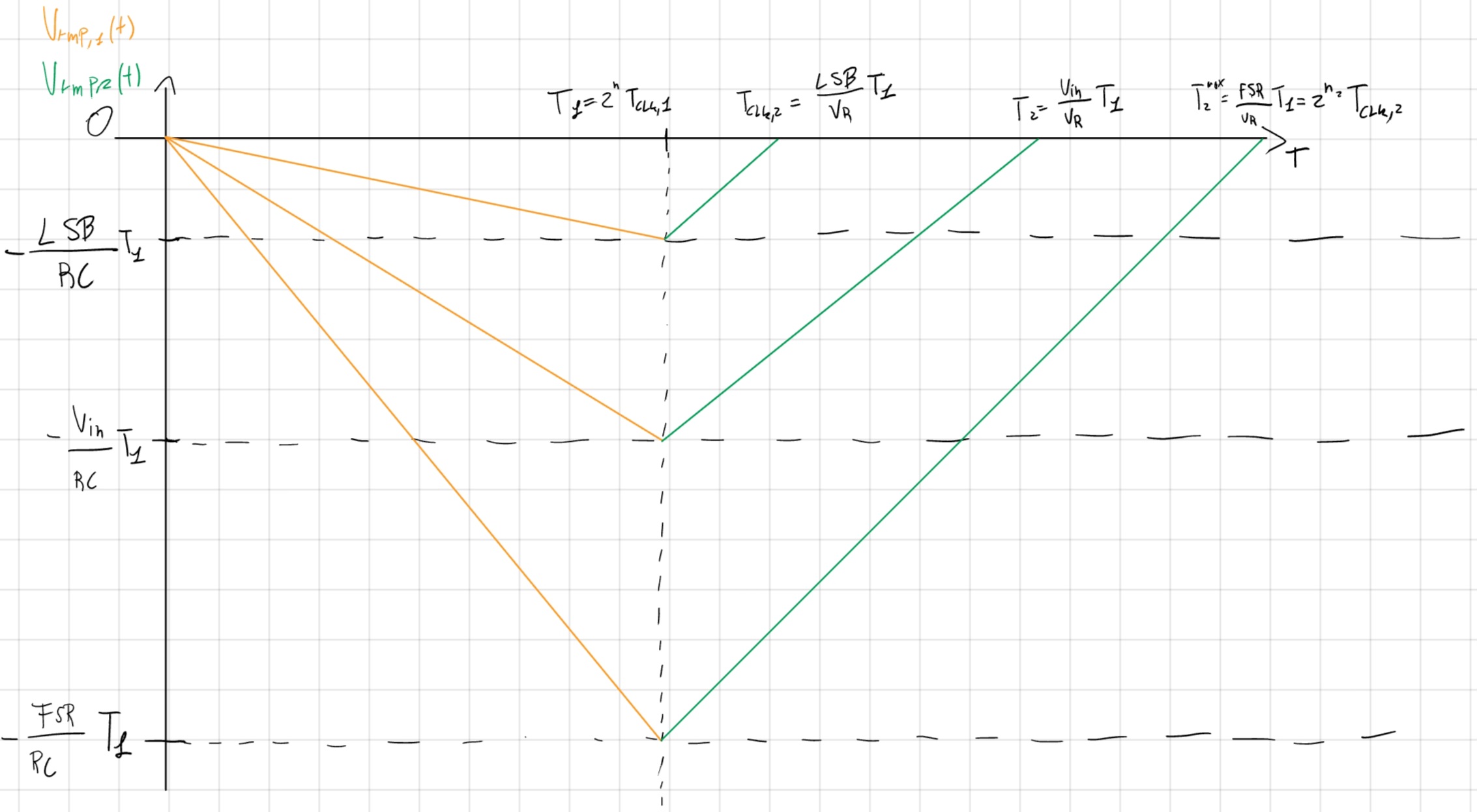
t \in [T_1,T_1+T_2]
- V_1 (t) = - \frac{V_{in}}{RC}T_1 + \frac{V_R}{RC} t
La conversione è compiuta quando V_1 (T_1 + T_2) = 0:
- - \frac{V_{in}}{RC}T_1 + \frac{V_R}{RC}T_2 = 0.
- T_2 = \frac{V_{in}}{V_R}T_1.
- T_{CONV} = T_1 + T_2 = T_1(1 + \frac{V_{in}}{V_R}).
LSB = \frac{T_{CLK,2}}{T_1}V_R \\ FSR = \frac{2^{n,2}T_{CLK,2}}{T_1}V_R \\ FSR = LSB \cdot 2^{n,2}
- Consumi bassi.
- Usa molti bit.
- T_{CONV} dipende da V.
- T_{CONV|MAX} = T_1 (1 + \frac{FSR}{V_R})
- V_R = FSR \to T_{CONV|MAX} = 2T_1
- DNL, INL, offset e Gain dipendenti dall’OpAmp.
- Filtro su V_{in}.
- FSR = Full Scale Range.
- LSB = Least Significant Bit.
V_1 (t) = - \frac{1}{C} \int_{0}^{t} \frac{V_{in} (t)}{R} dt \\ V_1(t) = - \frac{1}{RC} \int_{0}^{t} V_{in} (t) dt \\ \overline{V_{in}} = \int_{0}^{T_1} V_{in}(t) = valor medio.
V_1 (T_1) = - \frac{\overline{V_{in}}}{RC}
- L’integrale ha una funzione di filtro passa basso su V_{in}.
L’armonica generica a \frac{1}{T_1}:
- A_{\frac{1}{T_1}} sin(\frac{2 \pi t}{T_1} + \frac{\phi_1}{T_1})
- \int_{0}^{T_1} A_{\frac{1}{T_1}} sin(\frac{2 \pi t}{T_1} + \frac{\phi_1}{T_1}) dt = 0
Bisogna progettare T_1 affinchè sia minimo comune multiplo del periodo dei dist. presenti, più T_1 cresce:
- Più disturbi compensati.
- Più allunghiamo il tempo di conversione stesso.
10.4 Sample and Hold
Se introducessimo un circuito in grado di mantenere V^* che si vuole convertire per tutto il periodo T_{CONV} allora potremmo eccedere il limite di \frac{dV(t)}{dt} T_{CONV} < \plusmn \frac{LSB}{2}.
Questo circuito è chiamato “Sample and Hold” (S&H).
Nel sampling legge V (t) (V^*) e durante Hold viene mantenuta.
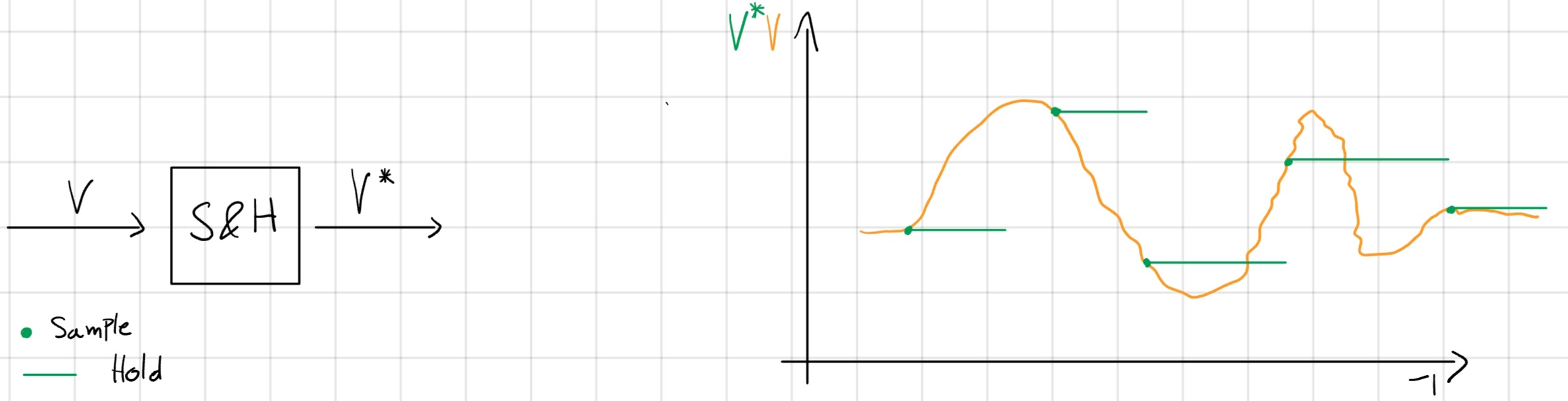
Idealità
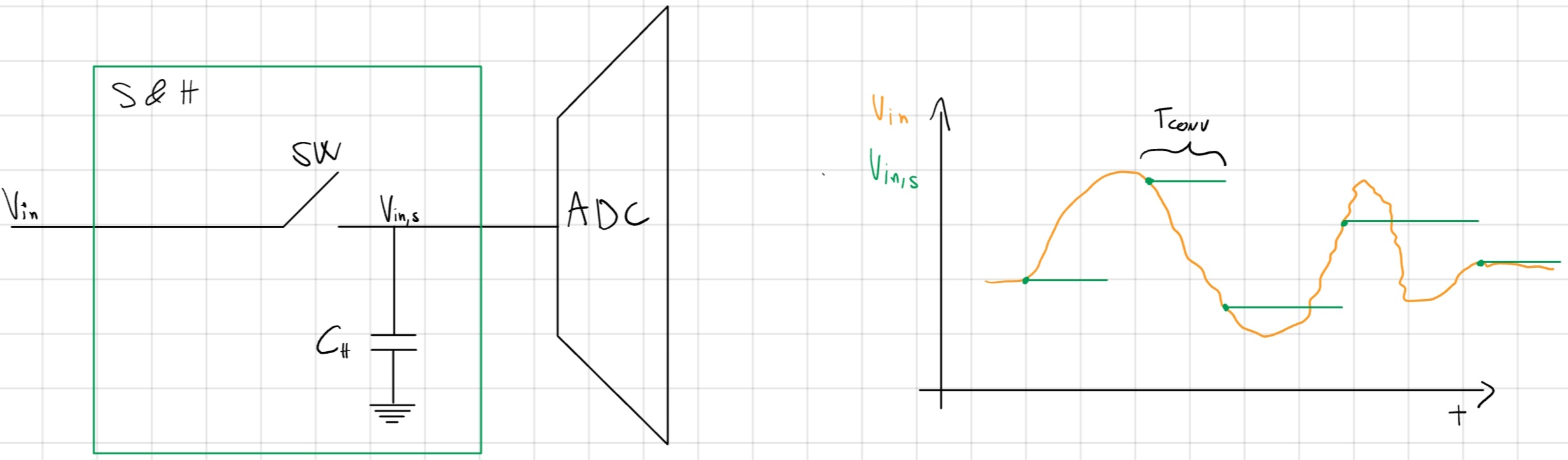
T_{CONV} indipendente dalla pendenza del segnale.
Realtà e Switch
Gli switch sono banali pass-transistor, con le stesse problematiche viste nel digitale, come ogni PT può essere di un NMOS o di un PMOS. In questo circuito portano in segnale analogico dall’ingresso alla C_H.
Switch NMOS
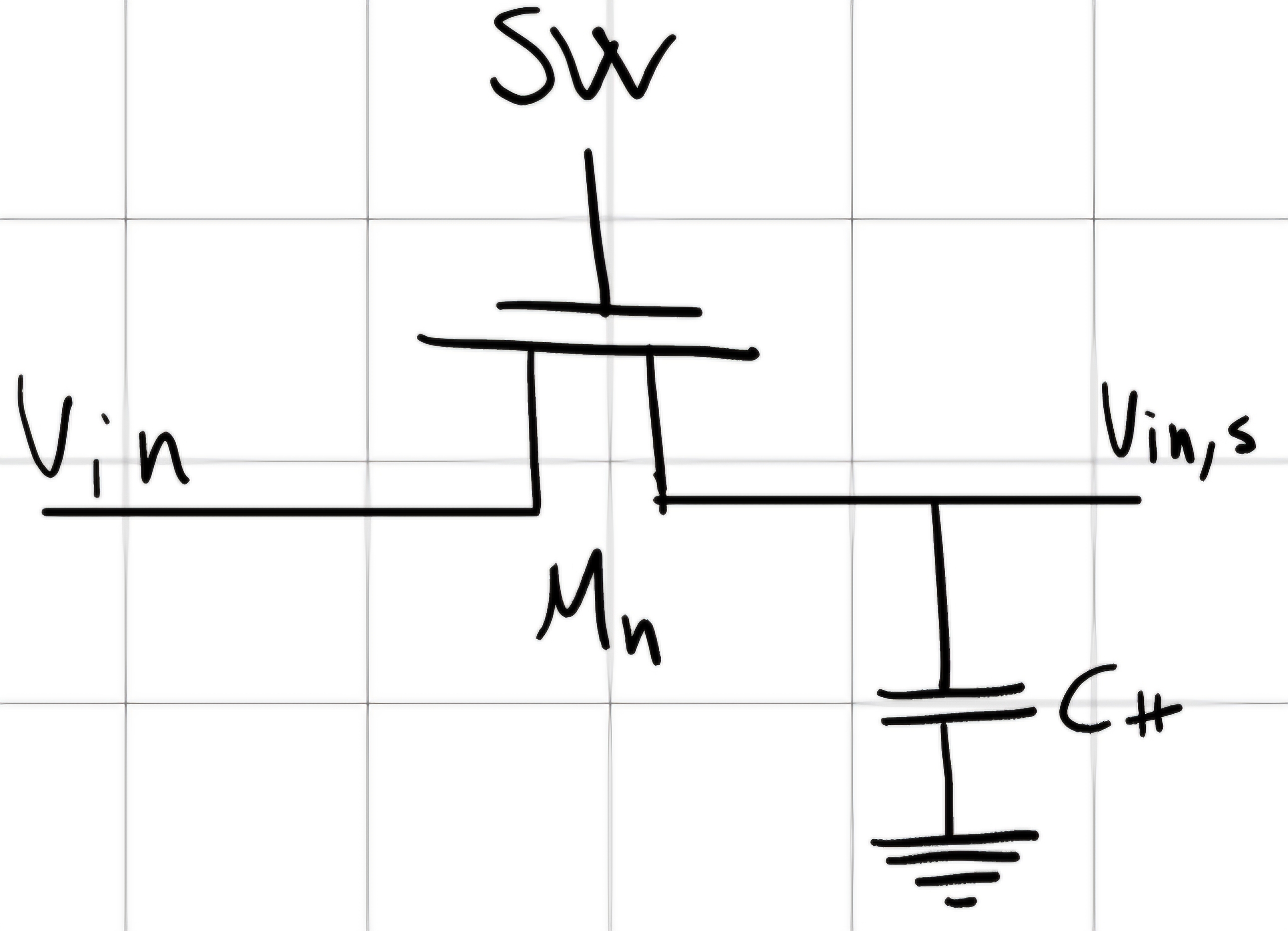
Considero V_{in} \in [V_{in}^{min}, V_{in}^{MAX}]:
- V_{SW}^{ON} > V_{in}^{MAX} + V_{T,n} per caricare C_H al massimo di V_{in}(t).
- V_{SW}^{OFF} < V_{in}^{min} + V_{T,n} per isolare C_H indipendente da V_{in} (t).
Switch PMOS
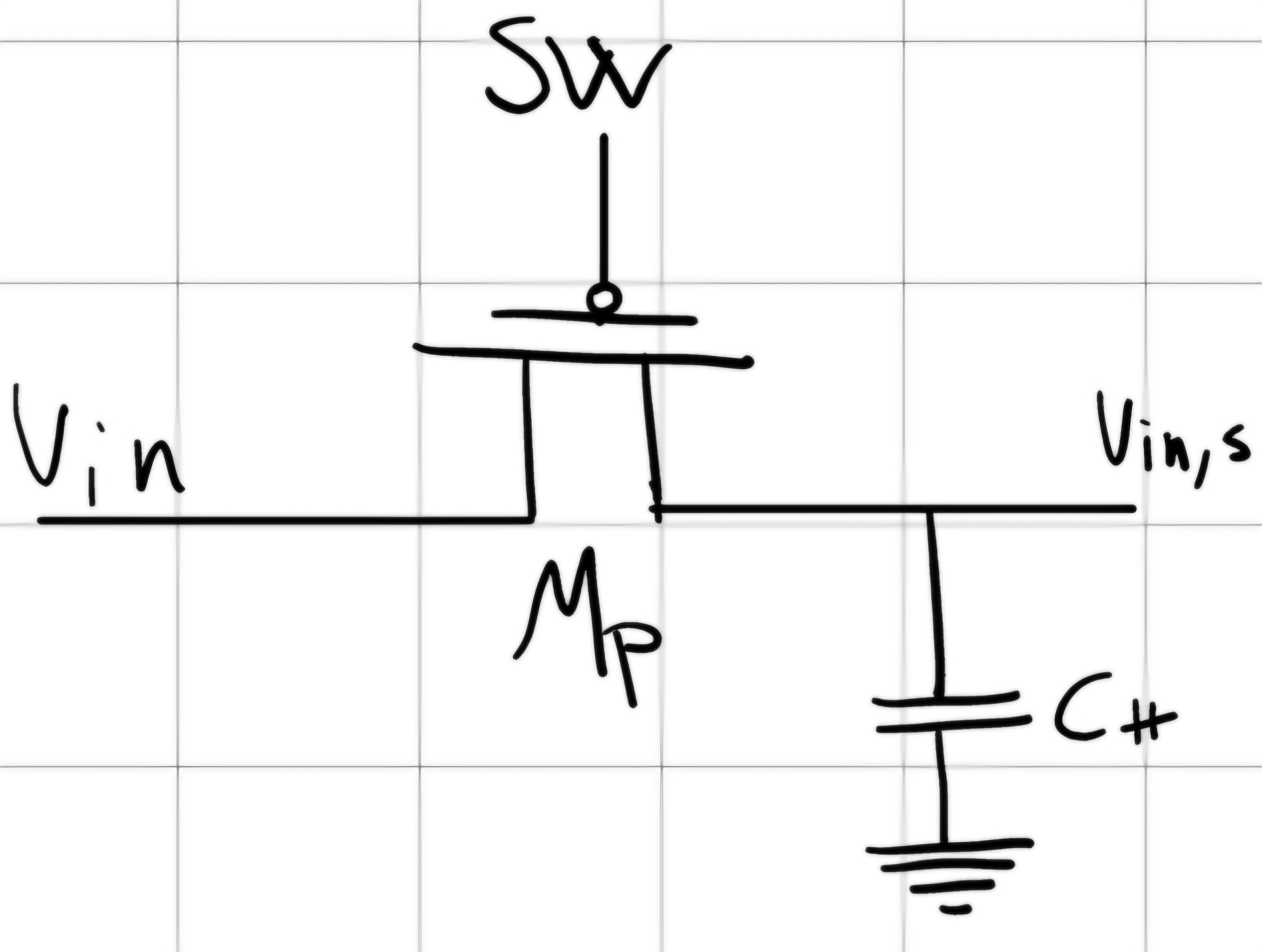
Con V_{in} \in [V_{in}^{min},V_{in}^{MAX}]:
- V_{SW}^{ON} < V_{in}^{min} + |V_{T,p}| scarica C_H fino a V_{in}^{min}.
- V_{SW}^{OFF} > V_{in}^{MAX} - |V_{T,p}| per isolare C_H indipendentemente da V_{in} (t).
Switch NMOS + PMOS
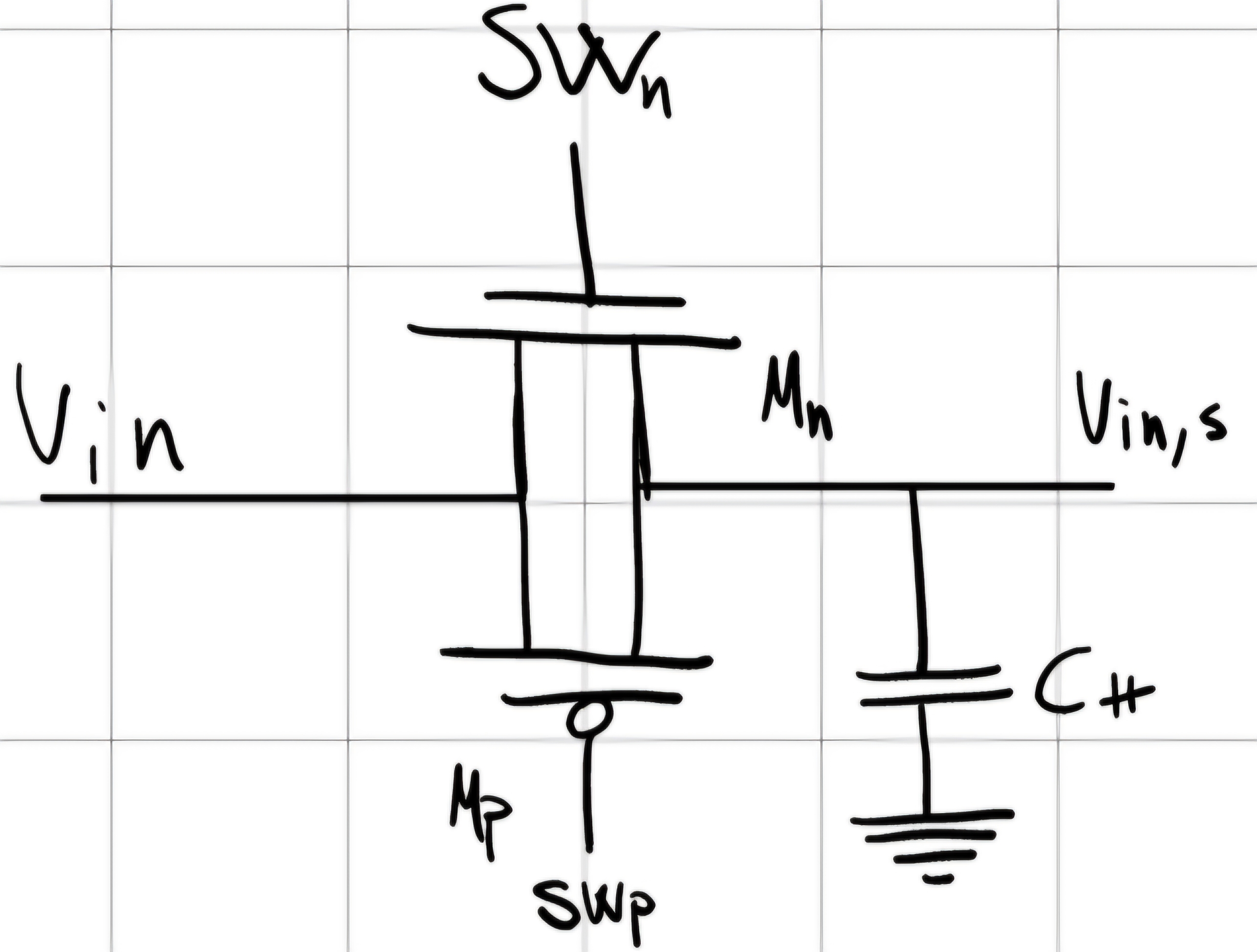
Con V_{in} \in [V_{in}^{min}, V_{in}^{MAX}]
- Le condizioni per ON/OFF sono uguali a prima.
- Basta che un MOS si accenda per portare V_{in} su V_{in,s} \implies per isolare C_H devono essere entrambi OFF.
- Basta che S_{Wn,p} siano complementari tra V_{in}^{MAX} e V_{in}^{min} per avere un MOS acceso.
Fase di Sample
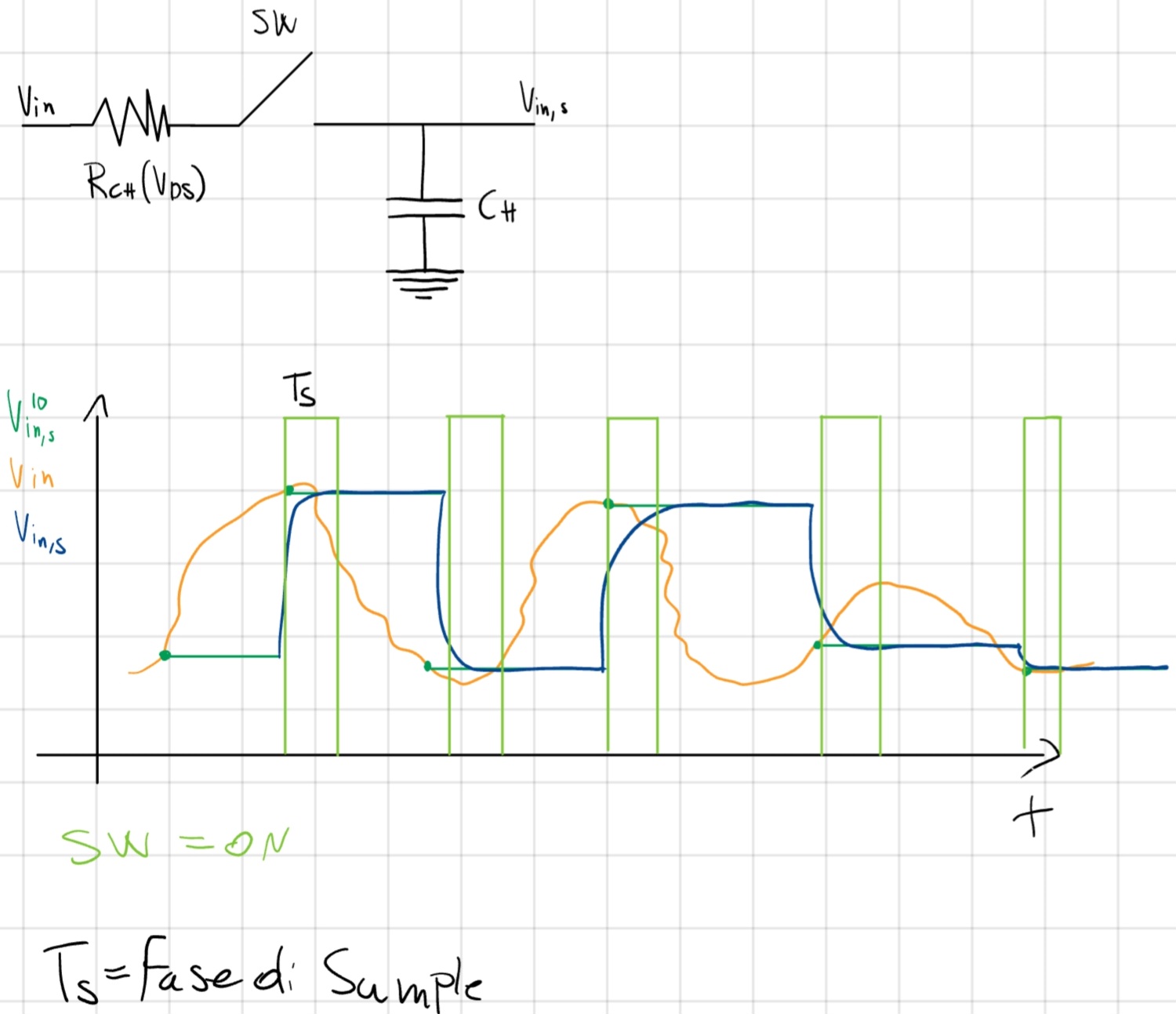
PMOS ed NMOS caricano/scaricano C_H:
Dobbiamo considerare i transitori.
La V_{SW} deve restare ON affinchè il transitorio non si carica completamente (pena decapitazione).
I MOS possono lavorare sia in ohmica che in saturazione.
Spesso si usano V_{SW}^{ON/OFF} >> dei valori minimi:
- quindi |V_{DS}| < |V_{OV}|, MOS in Ohmica.
Per R_{CH}(V_{DS}) si assume R_{CH}(0) per semplicità:
- R_{CH} (V_{DS}) = \frac{1}{2k(|V_{GS}| - |V_T| - |V_{DS}|)}
- R_{CH}(0) = \frac{1}{2k|V_{OV}|}
Teoricamente abbiamo:
- \tau_{SMP} = R_{CH}C_H
- T_{SMP} > 5 \tau_{SMP}
In realtà:
- V_{in,s} lett da un ADC che da un certo LSB.
- Quindi basta garantire un errore nella carica esponenziale inferiore a LSB, di solito \frac{LSB}{2} o un \varepsilon_{SMP}.
- Questo è il minimo T_{SMP} \implies per avere un errore inferiore a \varepsilon_{SMP} la fase deve essere > T_{SMP}^{min}.
Legenda:
\tau_{SMP} = R_{CH}C_H.
\varepsilon_{SMP} errore tollerato.
V^0 e V^\infty tensione di partenza e arrivo di V_{in,s} considerando SW sempre ON.
Supponiamo di iniziare a t_0 = 0:
- V_{in,s} (t) = V^0 + [V^\infty - V^0](1 - e^{-\frac{t}{\tau_{SMP}}})
- V_{in,s}(T_{SMP}^{min}) = V^\infty - \varepsilon_{SMP}.
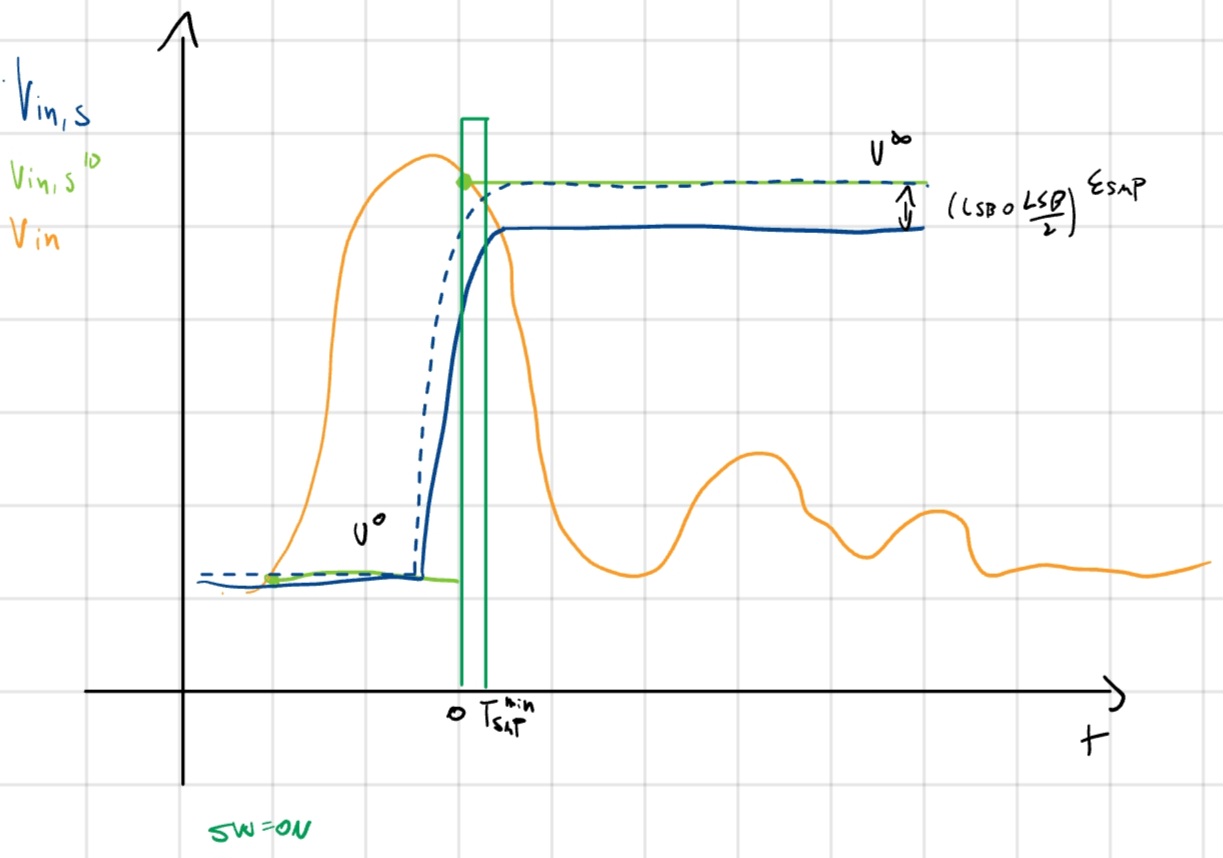
Esempio \varepsilon_{SMP} = LSB
V^0 = 0.
Considero 0 \to FSR.
- V_{in,s} (t) = FSR(1 - e^{-\frac{t}{\tau_{SMP}}})
- V_{in,s} (T_{SMP}^{min}) = FSR - \varepsilon_{SMP}
- T_{SMP}^{min} = \tau_{SMP} ln(\frac{FSR}{\varepsilon_{SMP}}) \xrightarrow{\varepsilon_{SMP} = LSB} \tau_{SMP} ln (\frac{FSR}{LSB}) = \tau_{SMP} \cdot n \cdot ln(2)
Fase di Hold
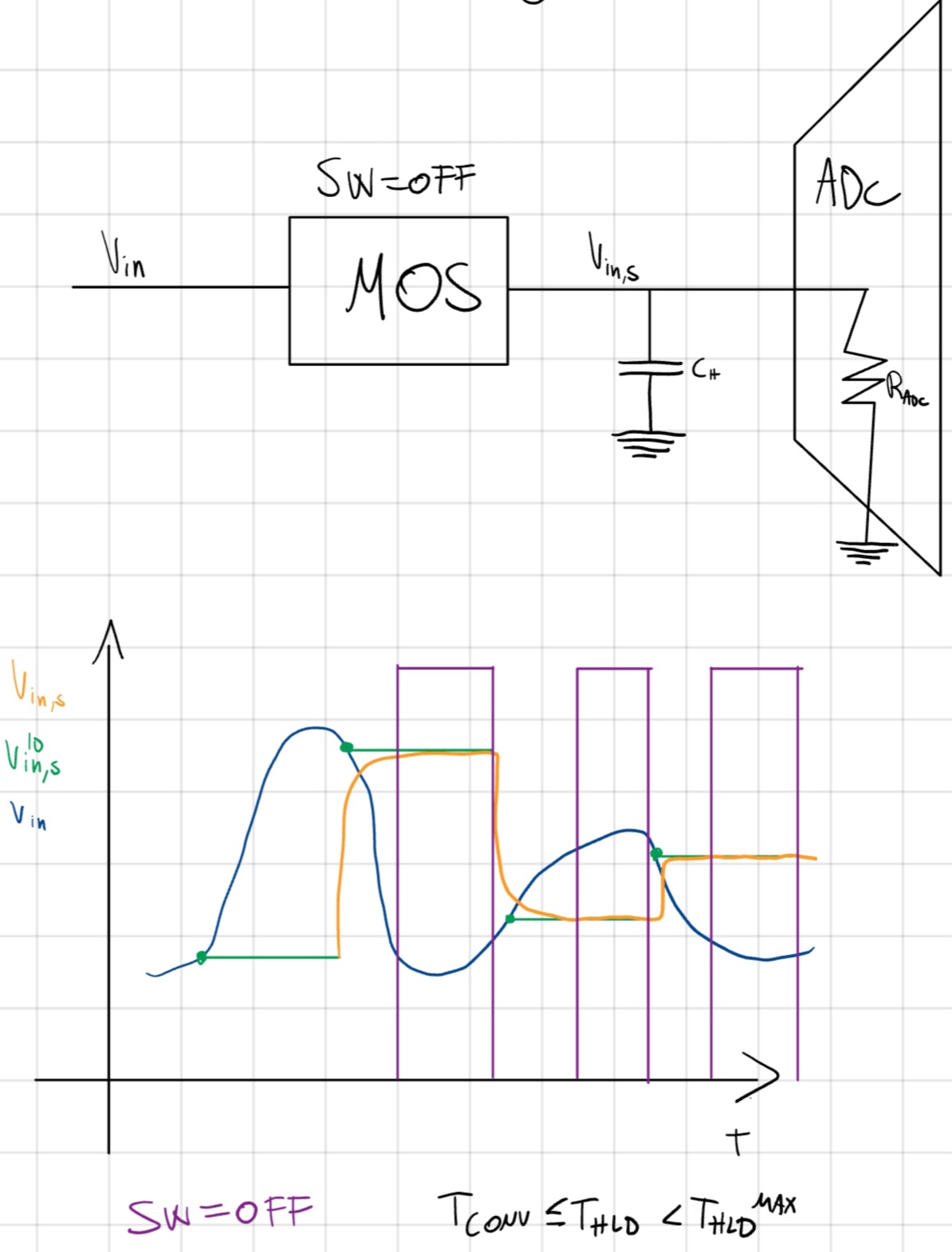
Se SW è OFF, fase di Hold, C_H si scarica su R_{ADC}:
- \tau_{HLD} = R_{ADC}C_H.
- T_{HLD} \geq T_{CONV} dell’ADC per garantire una buona conversione.
- Stesso discorso di prima per errore \varepsilon_{HLD}.
- T_{HLD} \in [T_{CONV}, T_{HLD}^{MAX}].
Considerazioni uguali a Sample.
- V_{in,s} (t) = V^0 + [V^\infty - V^0](1 - e^{-\frac{t}{\tau_{HLD}}})
- V_{in,s} (T_{HLD}^{MAX}) = V^0 - \varepsilon_{HLD}
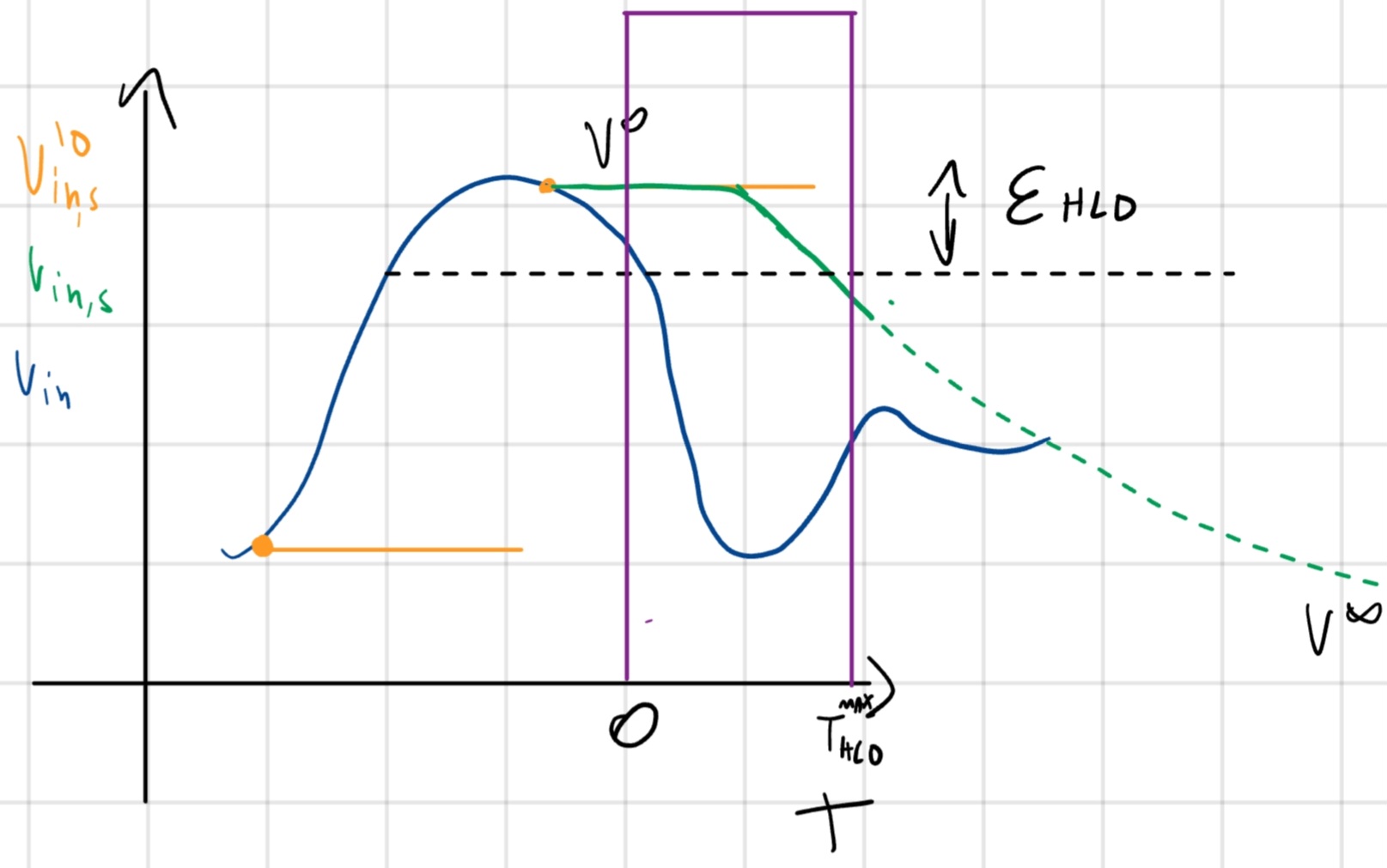
Esempio \varepsilon_{HLD} = LSB
- V^0 = 0
- FSR \to 0
- V_{in,s}(t) = FSR(1 - e^{-\frac{t}{\tau_{HLD}}})
- V_{in,s}(T_{HLD}^{MAX}) = FSR - \varepsilon_{HLD}
- T_{HLD}^{MAX} = \tau_{HLD} ln(\frac{FSR}{FSR - \varepsilon_{HLD}}) \xrightarrow{\varepsilon_{HLD} = LSB} \tau_{HLD} ln (\frac{2^n - 1}{2^n})
Buffer
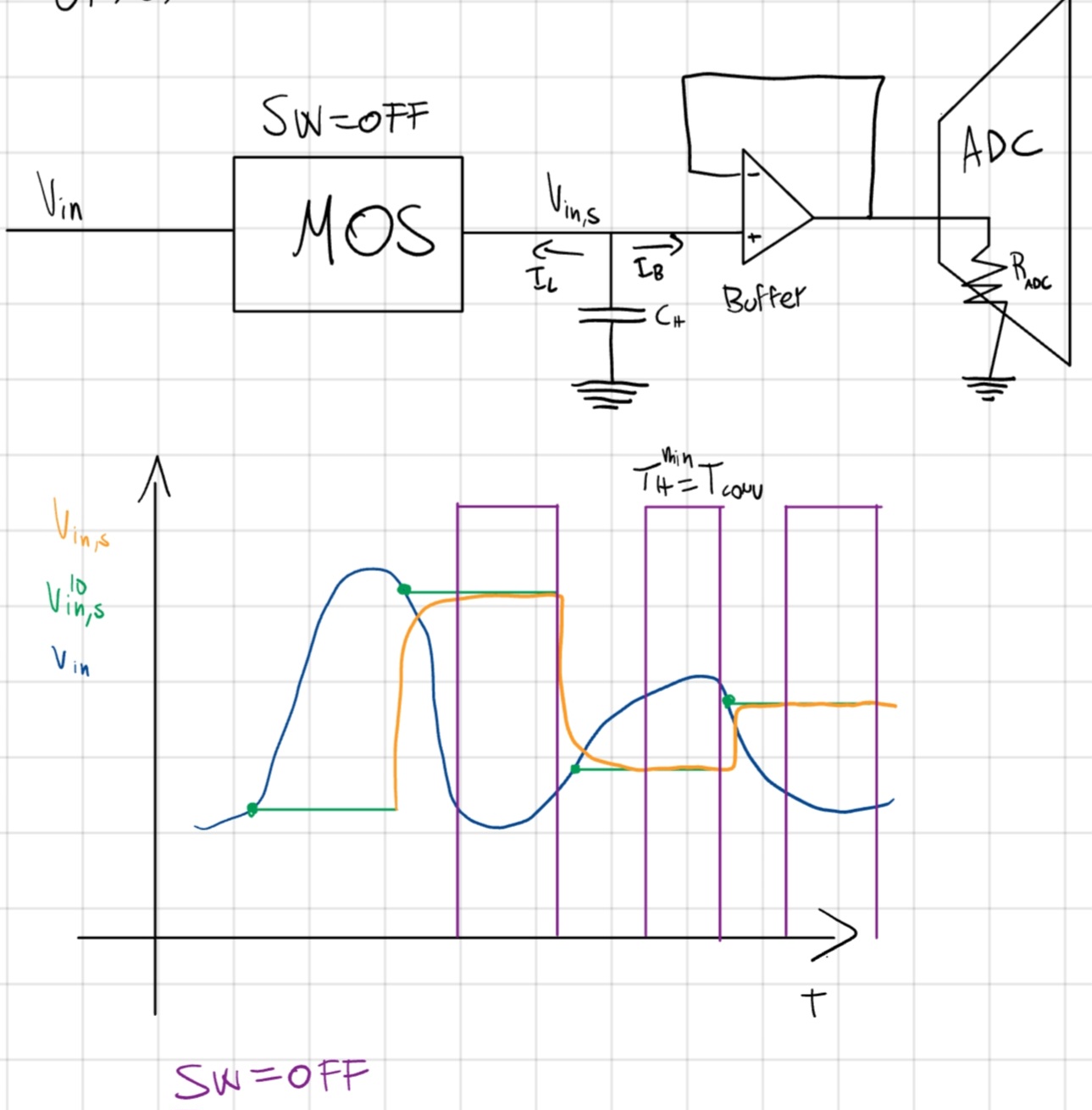
Se SW OFF, fase di Hold, C_H bufferizzato e separata dall’ADC.
- T_{HLD} \geq T_{CONV} dell’ADC.
- In T_{HLD}^{MAX} possiamo scaricare V_{in,s} solo se un errore \varepsilon_{HLD} pari LSB che NON dipendono da \tau_{HLD}.
- Abbiamo delle scariche a corrente costante dovute ai leakage (I_L) dello SW ed al bias (I_B) dell’Op.Amp.
Leakage
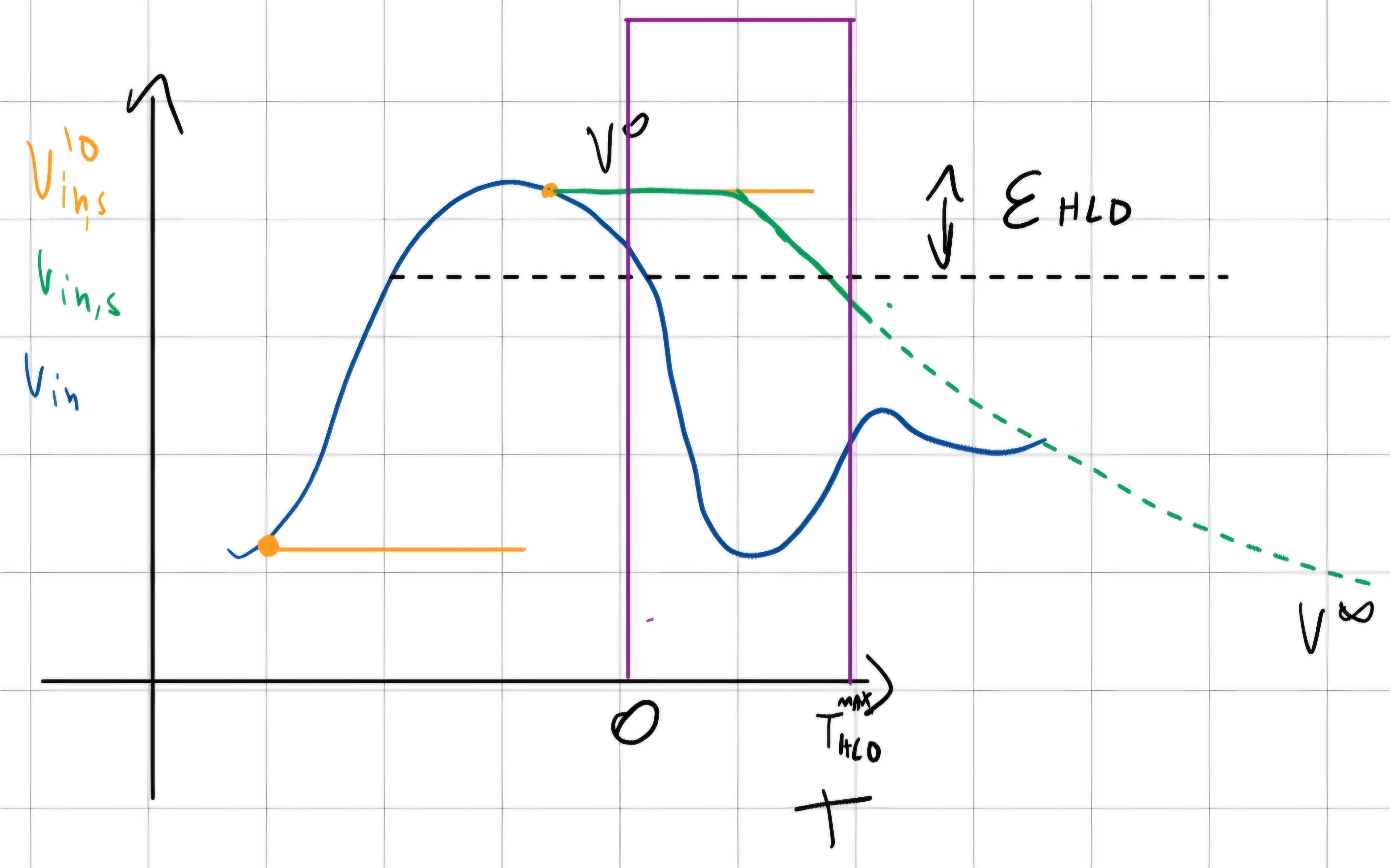
V_{in,s} (t) = V^0 - \frac{I}{C}t \\ V_{in,s} (T_{HLD}^{MAX}) = V^0 - \varepsilon_{HLD}
- I = I_L + I_B
- \varepsilon_{HLD}, errore gase di Hold.
- Iniziamo a t_0 = 0
V_{in,s} (t) = V^0 -\frac{I}{C}t \\ V_{in,s} (T_{HLD}^{min}) = V^0 \varepsilon_{HLD} \\ \frac{I}{C_H}T_{HLD}^{MAX} = \varepsilon_{HLD}
Considero \varepsilon_{HLD} = LSB. \\ T_{HLD}^{MAX} = \varepsilon_{HLD} \cdot \frac{C_H}{I} \xrightarrow{\varepsilon_{HLD} = LSB} LSB \cdot \frac{C_H}{I}
Con T_{HLD} \geq T_{CONV}, possiamo progettare C_H.
Progettazione
L’OpAmp avrà G_{reale} < G_{ID} dovuto ad A_0 finito.
- G_R = \frac{A_0}{1 + A_0}
- Con V: V \frac{A_0}{1 + A_0}
- Rispetto a G_{ID} \varepsilon = V \cdot G_{ID} - V \cdot G_R = \frac{V}{1 + A_0}
- Se \varepsilon < LSB possiamo usare G_{ID} per i calcoli.
- Nel caso pessimo è \frac{FSR}{1 + A_0} <^! LSB
- A_0 > \frac{FSR}{LSB} - 1 = 2^n - 1
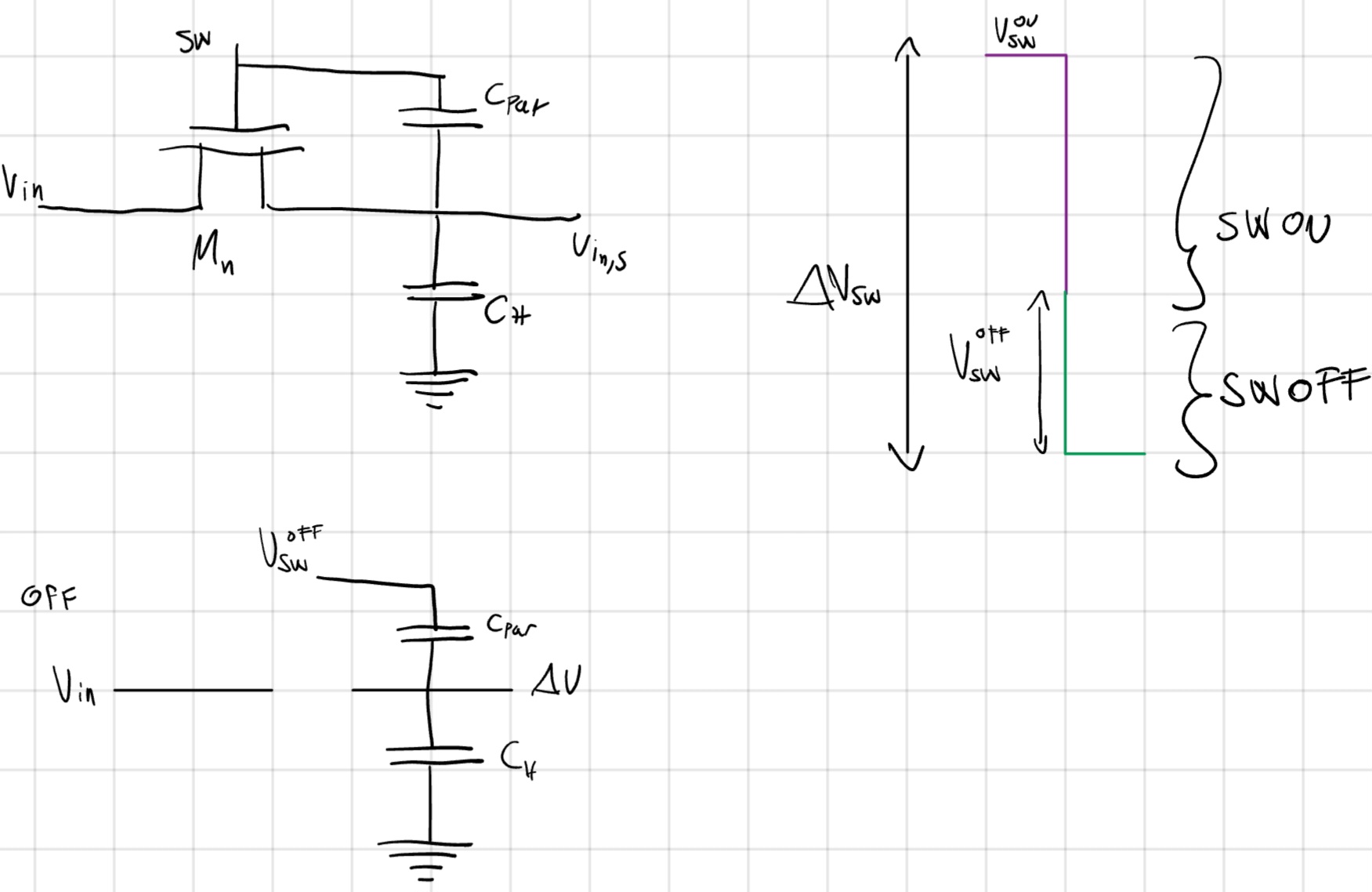
Charge Injection
Quando SW si ON/OFFA, le capacità parassite tra SW e C_H iniettano \Delta Q in C_H variando \Delta V su C_H.
\Delta V = \Delta V_{SW} \cdot \frac{C_{par}}{C_{par} + C_H}
Passando da HOLD \to SAMPLE
- V_{in} connesso a V_{in,s}, quindi \Delta V rimossa.
Passando da SAMPLE \to HOLD
- \Delta V diventa un \varepsilon.
- Di \Delta V_{SW} bisognerebbe considerare solo la parte di SW spenta.
- \Delta V = \Delta V_{SW}^{OFF} \cdot \frac{C_{par}}{C_{par} + C_H}
\Delta V <^! LSB quello impone limiti su:
- parassiti, se fissata C_H e \Delta V_{SW}.
- su C_H se fissati i parassiti e \Delta V_{SW}.
Campionamento
T_{ACQ} = T_{SMP} + T_{HLD}
T_{SMP}^{min} + T_{CONV} < T_{ACQ} < T_{SMP}^{min} + T_{HLD}^{MAX}
f_c = \frac{1}{T_{ACQ}}
Per il Teorema di Nyquist Shannon non si ha aliasing fino a:
- f_{MAX} \geq \frac{f_c}{2}
10.5 Finale
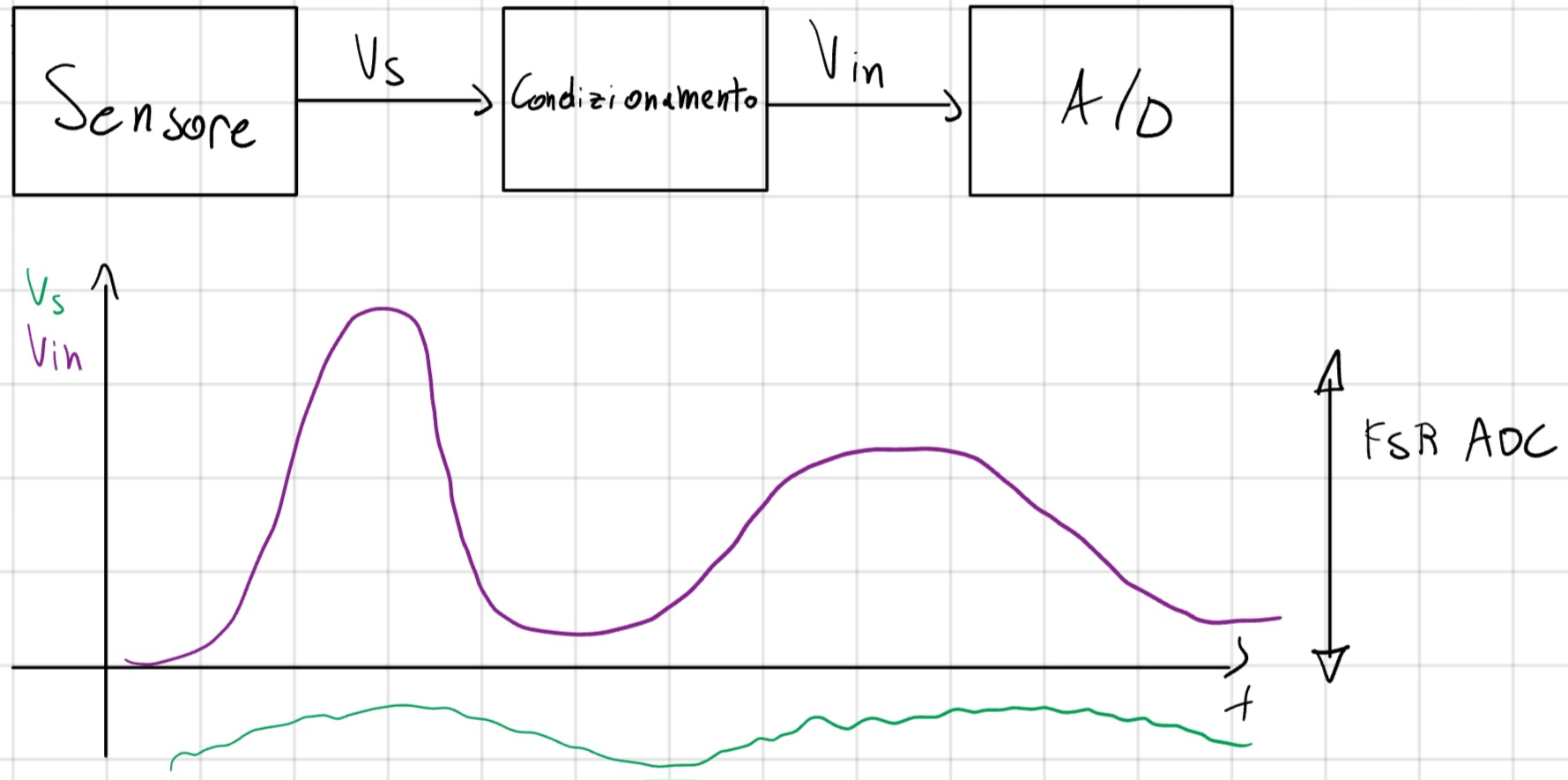
Blocco di Condizionamento
- Eliminare armoniche sopra \frac{f_c}{2}.
- Adatta la dinamica del segnale del sensore a quella dell’ADC.
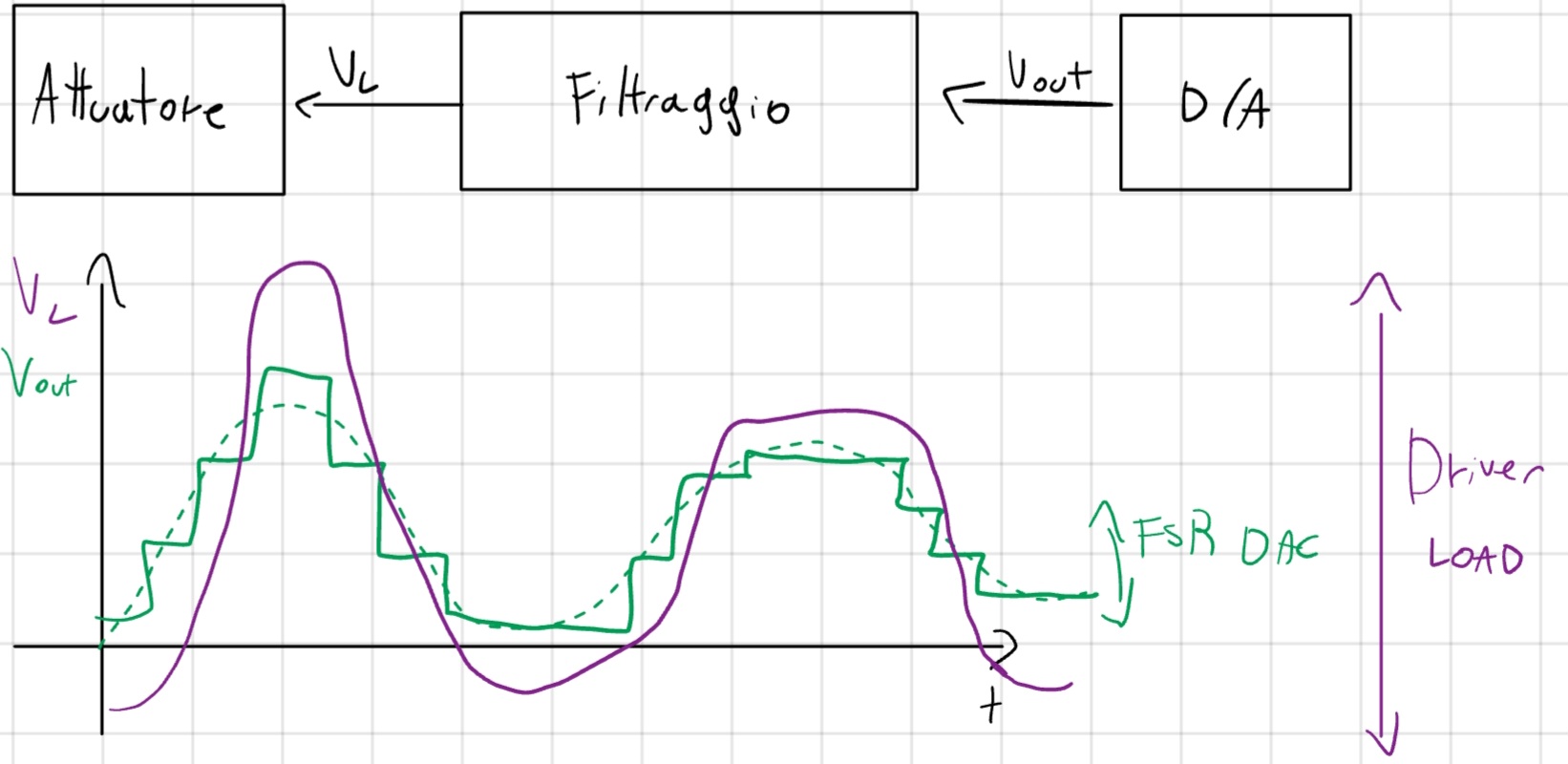
Filtraggio d’uscita
- Serve a smussare gli scalini in uscita dal DAC per avere un onda più smussata.
- Adatta eventualmente la dinamica del DAC con quella dell’attuatore.
Conclusioni
Con questo si conclude il corso di Fondamenti di Elettronica spero che i miei appunti possano risultare utili e comprensibili, nel caso non fosse così non esitate a segnalare.
Detto questo vi auguro un buono studio.
-NP